[백준] 1753번 - 최단경로

---

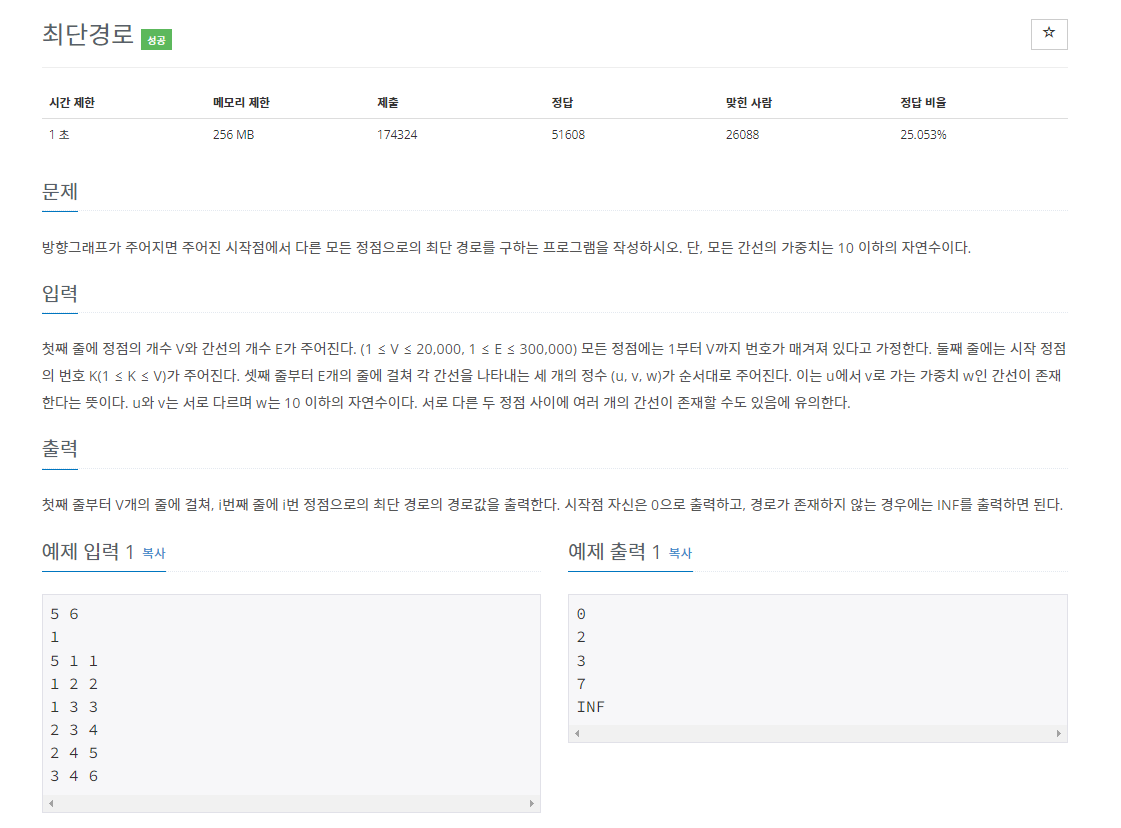
문제 분석

시작점과 다른 노드와 관련된 최단 거리를 구하는 문제로, 다익스트라 알고리즘의 가장 기본적인 문제이다.
따라서 다음과 같은 매커니즘을 통해 시작점으로 부터 각각의 노드까지의 최단거리를 구하면 된다.

1. 인접 리스트로 그래프 구현하기
   주어진 노드들 간의 연결을 인접리스트를 이용하여 표현해준다.
2. 최단 거리 리스트 초기화 하기
   최단 거리 리스트를 만들고 출발 노드의 인덱스에 해당하는 곳의 값은 0, 이외의 인덱스의 값들은 무한 으로 초기화 한다.
3. 값이 가장 작은 노드 고르기
   최단 거리 리스트에서 현재 값이 가장 작은 노드를 고른다.
4. 최단 거리 리스트 업데이트 하기
   선택된 노드의 연결된 에지의 값을 바탕으로 다른 노드의 값을 업데이트 한다.
   1단계에서 저장해 놓은 연결 리스트를 이용해 현재 선택된 노드의 에지들을 탐색하고 업데이트 하는 과정을 거친다.
   최단거리 업데이트 방법
   Min(선택 노드의 최단 거리 리스트의 값 + 에지 가중치, 연결 노드의 최단 거리 리스트의 값)
5. 과정 3 ~ 4를 반복해 최단 거리 리스트 완성하기
   모든 노드가 처리될 때까지 과정 3 ~ 4를 반복한다. 과정 4에서 선택 노드가 될때마다 다시 선택되지 않도록 방문리스트를 만들어 처리하는 것에 주의한다.

---

소스 코드

# 최단경로

from queue import PriorityQueue
import sys
input = sys.stdin.readline

V, E = map(int, input().split())
startNode = int(input())
minRoute = [sys.maxsize] * (V + 1)
minRoute[startNode] = 0
arr = [[] for _ in range(V + 1)]
visited = [False for _ in range(V + 1)]
queue = PriorityQueue()

for _ in range(E):
    start, end, value = map(int, input().split())
    arr[start].append((end, value))

queue.put((0, startNode))

while not queue.empty():
    minutes, nextNode = queue.get()
    if visited[nextNode]:
        continue
    visited[nextNode] = True

    for v in arr[nextNode]:
        minRoute[v[0]] = min(minRoute[v[0]], minRoute[nextNode] + v[1])
        queue.put((minRoute[v[0]], v[0]))

for i in range(1, V + 1):
    if visited[i]:
        print(minRoute[i])
    else:
        print("INF")