[백준 C++] 1167 트리의 지름

문제

트리의 지름이란, 트리에서 임의의 두 점 사이의 거리 중 가장 긴 것을 말한다. 트리의 지름을 구하는 프로그램을 작성하시오.

입력

트리가 입력으로 주어진다. 먼저 첫 번째 줄에서는 트리의 정점의 개수 V가 주어지고 (2 ≤ V ≤ 100,000)둘째 줄부터 V개의 줄에 걸쳐 간선의 정보가 다음과 같이 주어진다. 정점 번호는 1부터 V까지 매겨져 있다.

먼저 정점 번호가 주어지고, 이어서 연결된 간선의 정보를 의미하는 정수가 두 개씩 주어지는데, 하나는 정점번호, 다른 하나는 그 정점까지의 거리이다. 예를 들어 네 번째 줄의 경우 정점 3은 정점 1과 거리가 2인 간선으로 연결되어 있고, 정점 4와는 거리가 3인 간선으로 연결되어 있는 것을 보여준다. 각 줄의 마지막에는 -1이 입력으로 주어진다. 주어지는 거리는 모두 10,000 이하의 자연수이다.

출력

첫째 줄에 트리의 지름을 출력한다.

https://www.acmicpc.net/problem/1167

풀이

트리의 지름을 구하는 테크닉은 간간히 쓰여서 기억할 필요가 있다.

1. 트리의 임의의 정점으로부터 가장 먼(가중치합이 큰) 정점을 찾는다.
2. 찾은 정점으로부터 다시한번 가장 먼 정점을 찾으면 답이다.

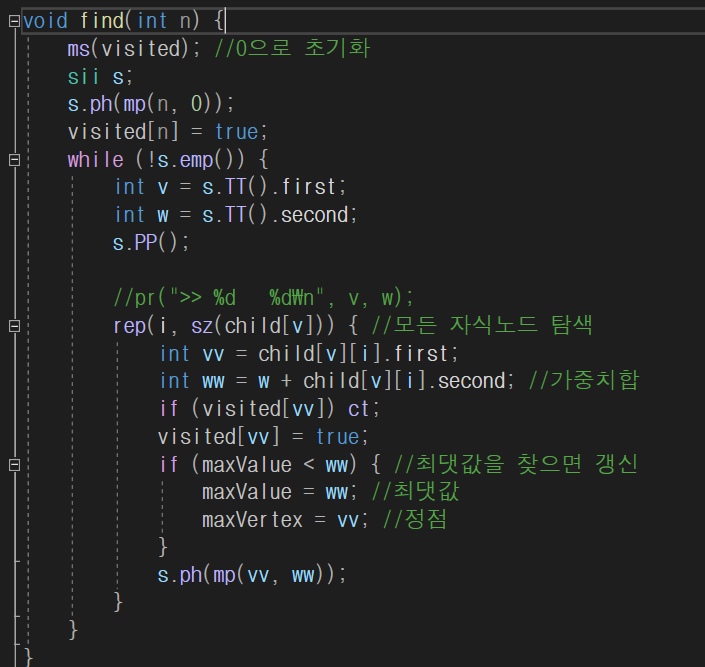DFS로 트리를 순회하며 가중치합이큰 가장 먼 정점을 찾는 코드이다. 물론 BFS로 진행해도 문제는 없다.

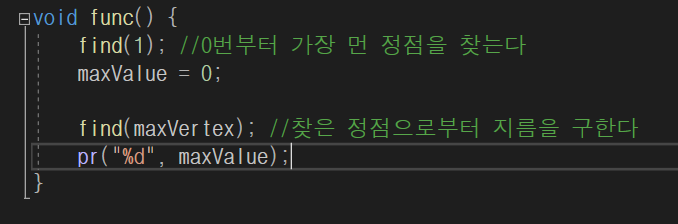임의의 정점으로 1을 선택, 가장먼 정점(maxVertex)을 찾은뒤 그 로부터 다시한번 먼 정점을 찾고 그 거리를 출력하면 끝

#define _CRT_SECURE_NO_WARNINGS 
#include <bits/stdc++.h>
#define mp std::make_pair 
#define mt std::make_tuple
#define dq std::deque
#define pq std::priority_queue
#define sw std::swap
#define ts(x) std::to_string(x)
#define tc() c_str()
#define sc(x, ...) scanf(x, ##__VA_ARGS__) 
#define pr(x, ...) printf(x, ##__VA_ARGS__) 
#define ins(x) insert(x)
#define pb(x) push_back(x)
#define pf(x) push_front(x)
#define PB() pop_back()
#define PF() pop_front()
#define ph(x) push(x)
#define TT() top()
#define PP() pop()
#define BB() back()
#define FF() front()
#define cls() clear()
#define emp() empty()
#define len(x) x.length()
#define sz(x) ((int)x.size()) //컨테이너에서 사용
#define ms(a) memset(a, 0, sizeof(a)) //0으로 초기화
#define rep(i, n) for(int i = 0; i < n ; i++)
#define rrep(i, r, n) for(int i = r; i < n ; i++)
#define rrrep(i, r, n) for(ll i = r; i < n ; i++)
#define _rrep(i, r, n) for(int i = r; i >= n; i--)
#define _rrrep(i, r, n) for(ll i = r; i >= n; i--)
#define each(x, a) for (auto& x: a)
#define all(x) x.begin(),x.end() //STL에서 전체 처리할때 사용
#define range(x, r, n) x.begin() + r, x.begin() + n //STL에서 구간설정
#define ct continue
#define br break
#define rt return
#define _TYF typedef //코드줄이기
#define _UG using
#define _TCE template <class T> inline
//#define MAX 
const int IMAX = INT32_MAX; const int IMIN = INT32_MIN;
const long long LMAX = LLONG_MAX; const long long LMIN = LLONG_MIN;
const long double PI = 3.141592653589793238462643383279502884197;
_UG std::vector; _UG std::stack; _UG std::queue; _UG std::tuple; _UG std::set; _UG std::list; _UG std::bitset; _UG std::string; _UG std::pair; _UG std::greater;
_UG std::tie; _UG std::sort; _UG std::max_element; _UG std::min_element; _UG std::fill; _UG std::stoi; _UG std::stod; _UG std::stof; _UG std::stol; _UG std::stold; _UG std::stoll; _UG std::stoul; _UG std::stoull;
//_UG std::max; //_UG std::min; //_UG std::map;
_TYF long long ll; _TYF unsigned long long ull;
_TYF pair<int, int> pii; _TYF pair<double, int> pdi; _TYF pair<int, double> pid; _TYF pair<double, double> pdd; _TYF pair<int, ll> pil;
_TYF pair<ll, int> pli; _TYF pair<ll, ll> pll; _TYF pair<ull, ull> pullull; _TYF pair<int, char> pic; _TYF pair<char, int> pci;
_TYF pair<char, char> pcc; _TYF pair<long, char> plc; _TYF pair<char, long> pcl; _TYF pair<ll, char> pllc; _TYF pair<char, ll> pcll;
_TYF pair<ull, char> pullc; _TYF pair<char, ull> pcull; _TYF pair<int, string> pis; _TYF pair<string, int> psi; _TYF pair<long, string> pls;
_TYF pair<string, long> psl; _TYF pair<ll, string> plls; _TYF pair<string, ll> psll; _TYF pair<ull, string> pulls;
_TYF pair<string, ull> psull; _TYF pair<string, string> pss;
_TYF tuple<int, int, int> tiii; _TYF tuple<int, int, int, int> tiiii;
_TYF tuple<ll, ll, ll> tlll; _TYF tuple<ll, ll, ll, ll> tllll;
_TYF vector<string> vs; _TYF queue<string> qs; _TYF stack<string> ss; _TYF dq<string> dqs; _TYF pq<string> pqs; _TYF dq<string> dqs;
_TYF vector<char> vc; _TYF queue<char> qc; _TYF stack<char> sc; _TYF dq<char> dqc; _TYF pq<char> pqc; _TYF dq<char> dqc;
_TYF vector<int> vi; _TYF queue<int> qi; _TYF stack<int> si; _TYF dq<int> dqi; _TYF pq<int> pqi; _TYF dq<int> dqi;
_TYF vector<pii> vii; _TYF queue<pii> qii; _TYF stack<pii> sii; _TYF dq<pii> dqii; _TYF pq<pii> pqii; _TYF dq<pii> dqii;
_TYF vector<tiii> viii; _TYF queue<tiii> qiii; _TYF stack<tiii> siii; _TYF dq<tiii> dqiii; _TYF pq<tiii> pqiii; _TYF dq<tiii> dqiii;
_TYF vector<tiiii> viiii; _TYF queue<tiiii> qiiii; _TYF stack<tiiii> siiii; _TYF dq<tiiii> dqiiii; _TYF pq<tiiii> pqiiii; _TYF dq<tiiii> dqiiii;
_TYF vector<pll> vll; _TYF queue<pll> qll; _TYF stack<ll> sll; _TYF dq<pll> dqll; _TYF pq<pll> pqll; _TYF dq<pll> dqll;
_TYF vector<tlll> vlll; _TYF queue<tlll> qlll; _TYF stack<tlll> slll; _TYF dq<tlll> dqlll; _TYF pq<tlll> pqlll; _TYF dq<tlll> dqlll;
_TYF vector<tllll> vllll; _TYF queue<tllll> qllll; _TYF stack<tllll> sllll; _TYF dq<tllll> dqllll; _TYF pq<tllll> pqllll; _TYF dq<tllll> dqllll;
_TCE T sq(T num) { rt num* num; }//제곱함수
_TCE T GCD(T num1, T num2) { if (num2 == 0) rt num1; rt GCD(num2, num1 % num2); }
_TCE T LCM(T num1, T num2) { if (num1 == 0 || num2 == 0) rt num1 + num2; rt num1* (num2 / GCD(num1, num2)); }
//STL 전용 초기화 함수들 ( ms~~ )
_TCE void msq(T& a) { while (!a.empty()) a.PP(); }//queue clear
_TCE void msv(T& a) { a.cls(); }//vector clear
_TCE void msdq(T& a) { a.cls(); }//deque clear
_TCE void msm(T& a) { a.cls(); }//map clear
_TCE void mss(T& a) { while (!a.empty()) a.PP(); }//stack, set clear
_TCE void mspq(T& a) { while (!a.empty()) a.PP(); }//priority_queue clear
//pii operator - (pii a, pii b) { rt pii(a.first - b.first, a.second - b.second); }
//bool operator <= (pii a, pii b) { rt a.first <= b.first && a.second <= b.second; } 
//bool operator >= (pii a, pii b) { rt a.first >= b.first && a.second >= b.second; } 
//bool operator < (pii a, pii b) { if (a == b) return false; rt a <= b; } 
//bool operator > (pii a, pii b) { if (a == b) return false; rt a >= b; }


int V;
vii child[100001]; //{정점, 정점간 가중치}
bool visited[100001];
int tail;
int maxValue; //지름 최댓값을 기록
int maxVertex; //최댓값일때 정점번호
void init();
void func();

void init() {
	sc("%d", &V);
	rep(i, V) { //정점갯수만큼 반복
		int cur, next, weight;
		sc("%d", &cur);
		while (1) {
			sc("%d", &next); //정점과입력
			if (next == -1) br;
			sc("%d", &weight); //가중치입력
			child[cur].pb(mp(next, weight)); //정점과 가중치를 기록
		}
	}

}

void find(int n) {
	ms(visited); //0으로 초기화
	sii s;
	s.ph(mp(n, 0));
	visited[n] = true;
	while (!s.emp()) {
		int v = s.TT().first;
		int w = s.TT().second;
		s.PP();

		//pr(">> %d   %d\n", v, w);
		rep(i, sz(child[v])) { //모든 자식노드 탐색
			int vv = child[v][i].first;
			int ww = w + child[v][i].second; //가중치합
			if (visited[vv]) ct;
			visited[vv] = true;
			if (maxValue < ww) { //최댓값을 찾으면 갱신
				maxValue = ww; //최댓값
				maxVertex = vv; //정점
			}
			s.ph(mp(vv, ww));
		}
	}
}

void func() {
	find(1); //0번부터 가장 먼 정점을 찾는다
	maxValue = 0;

	find(maxVertex); //찾은 정점으로부터 지름을 구한다
	pr("%d", maxValue);
}


int main(void) {
	init();
	func();

	rt 0;
}