풀이 방법

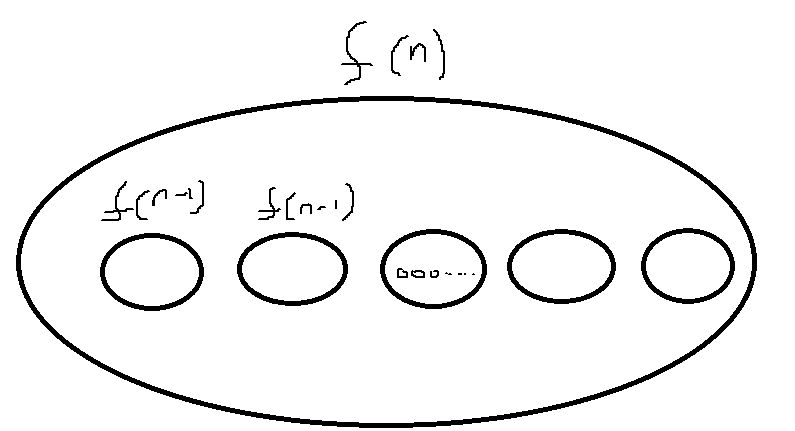
1. n에서의 총 1의 개수는 4^n임.
2. f(n)은 f(n - 1) f(n - 1) (0 * 5^(n - 1)) f(n - 1) f(n - 1) 이다.
   2.1 여기서 f(n - 1)에서 1의 개수는 4^(n - 1)이다.
   

3. 2번 식을 잘 이해한 후, 몫과 나머지를 이용하여 몫 2를 기준으로 오른쪽, 가운데, 왼쪽으로 나눈다.
4. 몫이 2라면 나머지는 전부 0이기 때문에 count할 필요가 없음.
5. 몫이 2보다 작다면 몫만큼 4^(n - 1)을 곱해주고, 나머지를 위의 과정 반복(재귀)
6. 몫이 2보다 크다면 몫 - 1 만큼 4^(n - 1)을 곱해주고, 나머지를 위의 과정 반복(재귀)
   6.1 왜 몫 -1이냐면 몫이 2일때의 숫자들은 전부 0이기 때문에 count 하지 않는다.

정답 : r까지의 1의 개수 - (l - 1)까지의 1의 개수

풀이 코드

def find_pos(n):
    i = 1
    while True:
        if 5 ** i > n:
            if i > 1:
                a, b = divmod(n, 5 ** (i - 1))
                if a > 2:
                    cnt = find_pos(b)
                    return cnt + (4 ** (i - 1)) * (a - 1)
                elif a == 2:
                    return (4 ** (i - 1)) * 2
                else:
                    cnt = find_pos(b)
                    return cnt + (4 ** (i - 1)) * a
            else:
                if n >= 3:
                    return n - 1
                else:
                    return n
        elif 5 ** i == n: 
            return 4 ** i
        else:
            i += 1
            
def solution(n, l, r):
    answer = find_pos(r) - find_pos(l - 1)
    
    return answer