정렬 알고리즘

‘정렬되지 않은 배열이 주어졌을 때, 어떻게 오름차순으로 정렬할 수 있을까?’

정렬을 하고 난 후, 검색을 시작해야 효율성이 극대화 된다.!

선택 정렬

1. 배열의 각 셀을 왼쪽부터 오른쪽 방향으로 확인하면서 어떤 값이 최솟값인지 결정한다. 한 셀씩 이동하면서 현재까지 가장 작은 값을 기록한다. (실제로는 그 인덱스를 변수에 저장!) 변수에 들어 있는 값보다 작은 값이 들어 있는 셀을 만나면 변수가 새 인덱스를 가리키도록 값을 대체한다. (제일 작은 값 검색)

2. 이제 최솟값이 어느 인덱스에 들어있는지 알았으므로 그 인덱스의 값과 패스스루를 처음 시작했을 때의 값을 교환한다. 패스스루를 시작했을 때 인덱스는 첫 패스스루에서는 인덱스 0일 것이고,(0 부터 시작) 두번째 패스스루에서는 인덱스 1일 것이다. (인덱스 0엔 최솟값이 들어가 있기 때문에)

3. 매 패스스루는 1,2단계가 이뤄진다. 배열 끝에서 시작하는 패스스루에 도달할 때까지 패스스루를 반복한다.

   선택정렬 도식화

선택정렬 코드

function selectionSort(array){
	for(let i=0; i<arrray.length-1; i++){
		let lowestNumberIndex = i;
		for(let j=i+1; j<array.length; j++){
			if(array[j] < array[lowestNumberIndex]){
				lowestNumberIndex = j;
			}
		}
		
		if(lowestNumberIndex != i){
			let temp = array[i];
			array[i] = array[lowestNumberIndex];
			array[lowestNumberIndex] = temp;
		}
	}
	return array;
}

• array.length -1 ⇒ 마지막 값을 시작하기 전에 이미 배열에 완전히 정렬되므로 마지막 값은 보지않아도 된다.

• if(lowestNumberIndex != i){ ⇒ 패스스루의 최솟값이 이미 올바른 위치에 있으면 (최솟값이 패스스루에서 만난 첫 번째 값인 경우) 아무것도 하지않아도 된다.

---

선택정렬의 효율성

비교 : 패스스루 내에서 각 값을 현재까지 찾은 최솟값과 비교
교환 : 최솟값을 올바른 위치에 있는 수와 교환

• 비교

원소 N개 일 때, → N-1 + N-2 + N-3 + …. + 1 비교를 한다.

• 교환

한패스스루 당 최대 1번 일어난다.
각 패스스루마다 최솟값이 이미 올바른 위치에 있느냐에 따라 교환을 안하거나 교환을 한번만 하기 때문이다.

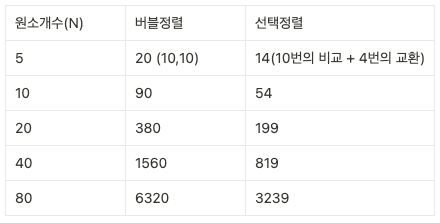
→ 표에서 비교한 바와 같이 선택정렬은 버블정렬보다 단계 수가 반 정도 작다. (선택 정렬이 두배정도 빠르다)

---

버블정렬 vs 선택정렬 (빅오표기법)

빅오표기법에서는 선택정렬과 버블정렬을 정확히 같은 방식으로 설명—???

(빅오표기법 - 데이터 원소가 N개 일 때 얼마나 많은 단계수가 필요한가,,)

선택정렬은 버블 정렬의 반단계 정도 소요가 되므로, 효율성은 약 O((N^2)/2) 정도이다. (이렇게 예상하기 쉽다. 버블정렬 - O(N^2)이기 때문에)

but, 선택정렬을 빅오로 표현하면, 버블정렬과 똑같이 O(N^2)이다.

빅오표기법은 상수를 무시한다. (지수가 아닌 수는 포함하지 않는다는 것을 단순히 수학적으로 표현한 문장)

즉, O((N^2)/2) === O(N^2) 둘 다 똑같다!

O(100N) === O(N) 똑같다.

왜 그럴까?

빅오 표기법의 특징 (상수 무시)

⇒ 빅오표기법의 특징 (일반적인 카테고리의 알고리즘 속도만 고려한다!!)

ex) 2층짜리 건물이다, 100층 건물이다. (x). ⇒ 저층 건물이다, 고층건물이다. (카테고리화)

빅오의 본질에서 살펴봤듯이 빅오표기법은 단지 알고리즘에 필요한 단계 수만 의미하지 않는다. 데이터가 늘어날 때 알고리즘 단계수가 장기적으로 어떤 궤적을 그리는지가 중요하다.!

O(N) 직선 성장, O(N^2) 지수성장

지수성장은 어떤 형태의 O(N) 과도 비교되지 않는 완전히 다른 카테고리다. O(N) 에 어떤 수를 곱하든 데이터가 커지다보면 언젠가 결국 O(N^2)이 더 느려진다.

즉, 빅오에서 서로 다른 카테고리에 속하는 두 효율성을 비교할 때, 일반적인 카테고리로 분류하는 것이 충분하다.

큰 일반적인 빅오의 카테고리

O(1), O(N), O(logN), O(N^2) …

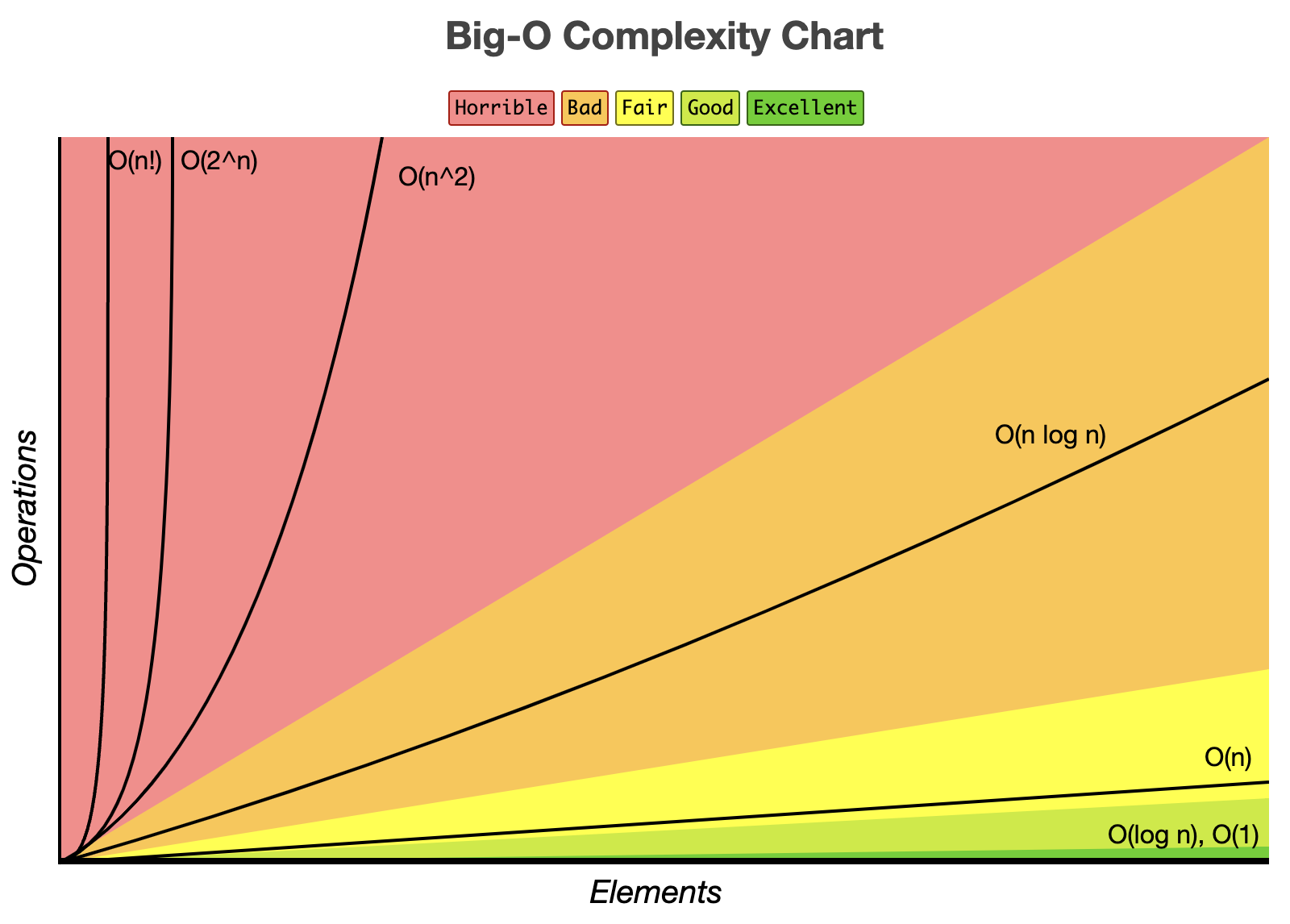
⇒ 따라서, 서로 다른 카테고리에 속하는 알고리즘을 대조할 때는 빅오가 완벽한 도구지만, 같은 카테고리에 속하는 다른 두 알고리즘이라면 어떤 알고리즘이 더 빠를지 알기 위해 더 분석해야한다.

상수 무시하는 예시 (시간복잡도)

• 짝수 출력 코드 (버전1)

function print_numbers_versions_one(upperLimit){
	number = 2;
	while(number <= upperLimit){
		if(number%2===0){
			print(number);
		}
		number+=1;
	}
}

• 짝수 출력 코드 (버전2)

function print_numbers_versions_one(upperLimit){
	number = 2;
	while(number <= upperLimit){
		print(number);
		number+=2;
	}
}

버전1의 경우, N단계가 걸린다. 즉, 시간 복잡도는 O(N) 이다.

버전2의 경우, N/2 단계가 걸린다. 시간 복잡도를 O(N/2) 라고 하고 싶겠지만, O(N)이다. (상수제외)

⇒ 보다시피, 버전2가 2배 빠르고 따라서 당연히 더 나은 방법이다. 이는 빅오표기법으로는 똑같이 표현되더라도 어떤 알고리즘이 더 빠른지 알아내려면 분석해야한다는 점을 보여준다.

버전1이 N단계 걸린다고 했는데, 정말 N일까?
루프안을 살펴보면 어려 단계가 일어난다.
if(number%2===0) 비교단계는 매 루프마다 일어나므로, N번 일어난다.
print(number) 출력단계로 짝수만 나오기 때문에, N/2 이다.
number+=1 매 루프마다 실행된다.
모든 단계가 다 중요하지만, 빅오용어로 단계를 표현할 때, 상수를 버리고 표현식을 단순화할 뿐이다.
2.5N 단계 → O(N) (상수제거)
모두 중요하지만, 상수를 제거함으로써, 루프 안에서 정확히 무슨 일이 이러나는지 보다는 실질적으로 루프가 실행되는 횟수에 더 초점이 가있다.