정렬 알고리즘

‘정렬되지 않은 배열이 주어졌을 때, 어떻게 오름차순으로 정렬할 수 있을까?’

정렬을 하고 난 후, 검색을 시작해야 효율성이 극대화 된다.!

삽입정렬

1. 첫번째 패스스루에서 임시로 인덱스 1의 값을 삭제하고, 이 값을 임시 변수에 저장한다. (인덱스 1자리 공백)

2. 다음으로 공백 왼쪽에 있는 각 값을 가져와 임시 변수에 있는 값과 비교하는 시프트 단계를 시작
   공백 왼쪽에 있는 값이 임시 변수에 있는 값보다 크면 그 값을 오른쪽으로 시프트한다.
   (공백이 왼쪽으로 이동하게 된다. === 왼쪽 끝에 있을 경우, 더 이상 왼쪽으로 공백을 시프트 못한다.)
   (임시로 삭제한 값보다 작은 값을 만나거나 배열의 왼쪽 끝에 도달해야 시프트 단계가 끝난다.)

3. 이제 임시로 제거한 값을 현재 공백에 삽입한다.

4. 1~3 단계가 하나의 패스스루이다. 배열의 마지막 인덱스에서 패스스루를 시작할 때까지 반복

삽입정렬 도식화

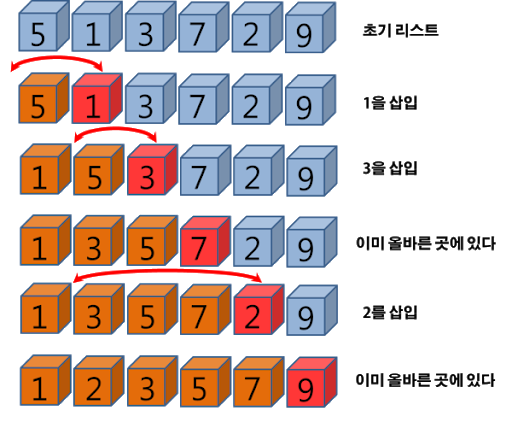
삽입정렬 코드

function insertion_sort(array){
	for (let index=1; index<array.length; index++){ // 매 루프가 하나의 패스쓰루
		temp_value = array[index];
		position = index - 1;
		
		while(position >= 0){
			if(array[position]>temp_value){
				array[position+1] = array[position];
				position = position - 1;
			}else{
				break;
			}
		}
		array[position+1] = temp_value; // 각 패스스루의 마지막 
	}


}

array[position+1] = temp_value; 각 패스스루의 마지막 단계 : temp_value를 공백에 삽입

삽입 정렬의 효율성

삭제, 비교, 시프트, 삽입 총 4가지를 고려해야한다.

• 비교 : 공백 왼쪽에 있는 값과 temp_value를 비교할 때마다 일어난다.
  최악의 시나리오 : 각 패스스루마다 temp_value값과 모든 수를 비교한다. (총 1+2+3+….N-1의 비교)
  ex. 5개 → 10번 비교, 10개 → 45번 비교, 20개일 때 190번 비교
  약, (N^2)/2 비교 단계가 일어난다.
• 시프트 : 값을 한 셀 오른쪽으로 옮길 때마다 일어난다. (배열이 역순으로 정렬돼 있다면 비교가 일어날 때마다 값을 오른쪽으로 시프트해야 하므로 비교 횟수만큼 시프트가 일어난다. )
  (N^2)/2 시프트 단계가 일어난다.
• 삭제 및 삽입 : 배열로부터 temp_value를 삭제 및 삽입하는 작업은 패스스루당 1번 → 패스스루 N-1 번 (삭제하고 삽입해줘야하기 때문에)
  삭제 : N-1, 삽입 : N-1

총, N^2 + 2N - 2 단계

시간 복잡도 - O(N^2)

평균시나리오

• 삽입정렬
  최악의 시나리오 : N^2
  최선의 시나리오 : N (패스스루당 한번의 비교만 있을 뿐 어떤 데이터도 시프트 x)

평균 : (N^2)/2

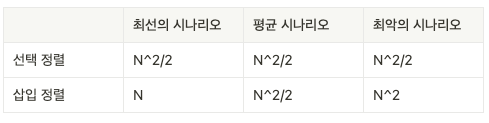
거의 정렬된 데이터 : 삽입 정렬
대부분 역순으로 정렬된 데이터 : 선택 정렬

삽입 정렬 & 선택 정렬 실제 예제

• 교집합 구하는 알고리즘
  ex) [3,1,4,2] <-> [4,5,3,6] ===> [3,4] 나와야함.

function intersection(firstArray, secondArray){
	let result = [];
	
	for(let i=0; i < firstArray.length; i++){
		for(let j=0; i < secondArray.length; j++){
			if(firstArray[i]===secondArray[j]){
					result.push(firstArray[i]);
			}
		}
	}
	return result;
}

두 배열의 크기가 같고 이때, 배열의 크기가 N이면 N^2 번의 비교를 수행한다.

두 배열의 크기가 다르면, 가령 N과 M 이라 하면, 이 함수의 효율성은 O(N*M) 이다.

⇒ 이 알고리즘의 성능을 향상시킬 수 있는 방법은.?

? : 두 배열에 공통 값이 있다면 첫번째 배열의 어떤 값을 꼭 두번째 배열의 모든 원소와 비교하지 않아도 된다.
두번째 배열에서 공통된 값을 찾았다면 그 이후에 들어있는 값들은 비교할 필요가 없다! (이미 result에 값을 추가했기 때문에)

• 교집합 구하는 알고리즘 (수정)

function intersection(firstArray, secondArray){
	let result = [];
	
	for(let i=0; i < firstArray.length; i++){
		for(let j=0; i < secondArray.length; j++){
			if(firstArray[i]===secondArray[j]){
					result.push(firstArray[i]);
					break;
			}
		}
	}
	return result;
}

break를 추가함으로써 안쪽 루프를 짧게 끝낼 수 있고, 단계를 절약할 수 있다.

최악의 경우를 대비하는 것도 좋지만, 대부분은 평균적인 경우가 일어난다!