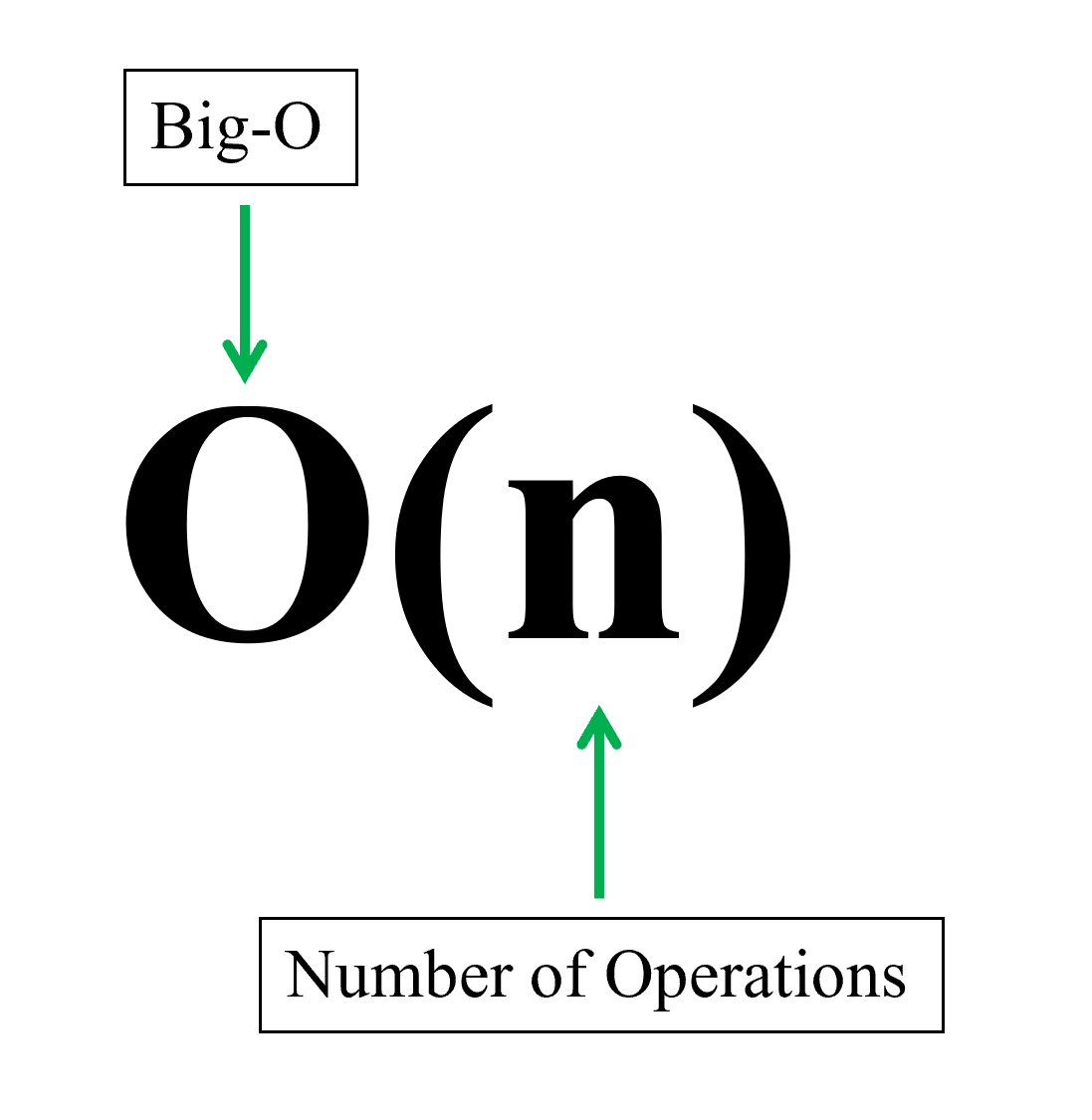🥛 빅오 표기법
서로 간에 시간 복잡도를 쉽게 소통할 목적으로 자료 구조와 알고리즘의 효율성을 간결하고 일관된 언어로 설명하기 위한 수학적 개념
(ex. 배열 N개의 원소가 있을 때, 선형검색에 N단계가 필요)
빅오의 본질
→ 데이터가 늘어날 때 알고리즘의 성능이 어떻게 바뀌는지 뜻함.
알고리즘에 필요한 단계 수만 알려주지 x, 데이터가 늘어날 때, 단계 수가 어떻게 증가하는지 설명
즉, 원소가 N개 일 때, 알고리즘에 항상 3단계가 필요하다면 → O(1) 이다. (O(3) x)
O(1) : 상수시간을 갖는 알고리즘 (항상 상수단계만 필요)
선형검색
→ 최선의 시나리오 : O(1)
→ 최악의 시나리오 : O(N)
빅오 표기법은 일반적으로 최악의 시나리오,
→ 비관적인 접근이 유용한 도구일 수 있기 때문이다.!
빅오표기법,,
알고리즘의 효율성을 표현하는 훌륭한 도구
빅오표기법을 사용하면 세상에 존재하는 범용 알고리즘을 비교할 기회가 생긴다,,!
이진검색의 시간복잡도
O(logN) : 데이터가 2배로 증가할 때마다 한 단계씩 늘어나는 알고리즘
→ 아주 조금씩 증가하는 곡선을 그리고 있다.! O(1)보다는 덜 효율적이지만, O(N)보다는 훨씬 효율적이다.
📌 로가리즘 : 지수와 역의 관계
2^3 = 222 = 8
log(2)8 은 2^3의 역이다. 즉, 2를 3번 곱해야 8이 나오므로 log(2)8 = 3이다.
log(2)64 = 6
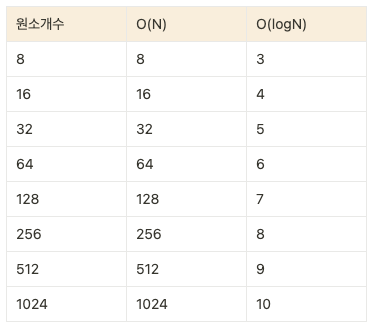
O(logN) 은 데이터 원소가 N개 있을 때, 알고리즘에 logN단계가 걸린다는 의미다.
(원소가 8개 이면 log8 =3 이므로, 이 알고리즘은 3단계가 걸린다.)
→ 이진검색은 정확히 이렇게 동작한다. (특정항목을 찾을 때, 정답 수에 도달할 때까지 배열의 셀을 계속해서 반으로 나누며 범위를 좁혀 나간다.)
간단히 말해, O(logN) 은 원소가 하나가 될 때까지 데이터 원소를 계속해서 반으로 줄이는 만큼의 단계 수가 걸린다는 뜻이다.
마무리
복잡하지 않는 코드일지라도, 뭔가를 하는 코드는 모두 엄밀히 알고리즘, 즉 문제를 풀어나가는 절차