알고리즘

어떤 과제를 완수하는 명령어 집합

알고리즘 기준 : 비정렬된 배열 vs 정렬된 배열 (에 따라서 많이 달라짐)

---

자료구조 연산 종류 효율성 판단

• 삽입

삽입에 있어 정렬된 배열이 전형적인 배열보다 덜 효율적

삽입 위치에 따른 영향

값이 배열 앞쪽에 위치:

• 비교가 줄어들지만 이동이 늘어남: 삽입 위치를 찾는 탐색은 짧지만, 삽입 위치 이후의 모든 값을 이동해야 함.
• 최악의 경우 모든 값을 이동해야 함(O(N)).

값이 배열 뒤쪽에 위치:

• 비교가 늘어나지만 이동이 줄어듦: 삽입 위치를 찾는 탐색은 길어지지만, 이동할 값이 적음.
• 삽입할 값이 마지막에 위치하면 이동 없이 바로 추가 가능(N+1 단계).

---

• 검색

비정렬 배열

• 원하는 값이 배열 어디든 있을 수 있으므로, 모든 원소를 하나도 빠짐없이 검색해야한다. 배열의 끝에 도달하기 전에 검색을 멈추는 경우는 원하는 값을 찾았을 때 뿐이다.

정렬된 배열

• 순회하던 요소가 원하는 값보다 크면 배열에 원하는 값이 없다는 뜻이므로 검색을 중단한다.
  이러한 관점에서 보면 선형 검색은 특정 상황에서 전형적인 배열보다 정렬된 배열에서 단계수가 더 적게 걸린다. 하지만 찾으려는 값이 배열의 마지막 값이거나 마지막 값보다 크면 마찬가지로 모든 셀을 검색해야 끝난다.

선형검색이란?
데이터를 순서대로 하나씩 확인하면서 원하는 값을 찾는 검색 알고리즘

이진검색이란?
정렬된 배열에서 선형검색보다 훨씬 빠른 이진검색(알고리즘)
배열의 크기만큼 절반을 나누고, 그 mid_point가 원하는 값보다 작은지, 큰지를 바탕으로 왼쪽,오른쪽 이동하여 범위를 계속 좁혀 나가는 방식이다.

const binary_search(array, search_value){
	lower_bound = 0;
	upper_bound = array.length - 1;
	
	while(lower_bound<=upper_bound){
		mid_point = (upper_bound + lower_bound) / 2
		value_point = array[mid_point]
		
		if(value_point === search_value){
			return mid_point // index 추출
		}else if(value_point < search_value){
			lower_bound = mid_point+1
		}else if(value_point > search_value){
			upper_bound = mid_point-1
			}
		}
	return null
}

-> while 문의 루프는 search_value를 찾을 . 수 있는 원소가 남아 있을 때까지 수행된다.

---

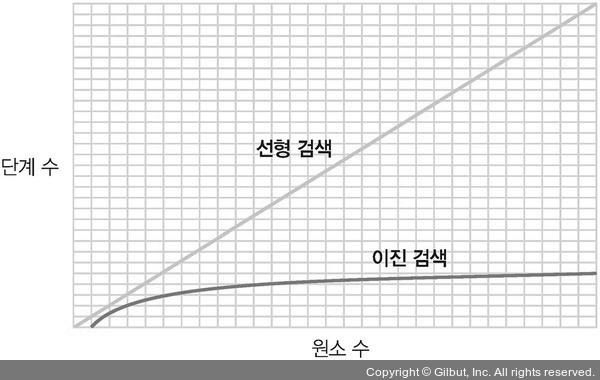
이진검색 vs 선형검색

100개의 값을 갖는 배열에서 검색에 필요한 최대 단계 수

선형검색 - 100단계

이진검색 - 7단계

이진검색을 쓰면 추측할 때마다 검색해야 . 할 셀 중 절반을 제거할 수 있다.

즉, 정렬된 배열의 크기를 두 배로 늘릴 때마다 이진 검색에 필요한 단계 수가 1씩 증가하는 패턴이 보인다. 값을 확인할 때마다 검색할 원소의 절반을 제거한다. (데이터를 2배로 늘릴 때마다 이진 검색 알고리즘에서는 최대 한 단계만 더 추가하면 된다.) (but, 선형검색에서는 원소 수만큼의 단계가 필요하다)

etc) 정렬된 배열에 이진검색을 쓸 수 있다고 해서 항상 정렬된 배열을 써야하는 것은 아니다. 데이터 검색은 거의 없고 데이터를 추가하기만 한다면 삽입을 더 빠르게 처리하는 배열이 더 나은 선택일 수도 있다.

"경쟁 알고리즘 간 성능을 분석하는 방법은 각각에 필요한 단계 수를 세는 것"