한줄요약

NGCF에서 feature transformation, nonlinear activation을 삭제한 모델이 여기서 소개할 LightGCN이다.
(NGCF 모델의 업그레이드 버전이니 "Neural Graph Collaborative Filtering" 논문을 완벽히 이해했다고 가정하고 리뷰하니 반드시 해당 논문을 읽고 오셔야합니다.)

ABSTRACT

저자들은 GCN에서 feature transformation과 nonlinear activation이 collaborative filtering에 거의 기여하지 않고, 심지어는 성능을 감소시킨다는 것을 발견했다. 여기서는 GCN을 단순화하여 추천에 더 간결하고 적합하게 하는 LightGCN이라는 모델을 소개한다. LightGCN은 GCN의 가장 필수적인 neighborhood aggregation만을 사용한다. LightGCN은 선행 연구 논문 모델인 NGCF의 성능을 능가한다.

1 INTRODUCTION

저자들은 NGCF의 모델 설계 구조가 무겁다고 주장한다. GCN은 원래 각 node가 풍부한 feature를 가지고 있는 graph의 node classification을 위해 제안된 반면에 collaborative filtering에서는 user-item 사이의 one-hot ID로만 설명된다. 이 경우에는 현대 신경망의 key인 performing multiple layers of nonlinear feature transformation은 어떠한 이득도 가져와주지 않을 것이다. 그래서 저자들은 본인들의 생각을 입증하기 위해 NGCF에 대한 ablation studies를 하는 것으로 시작한다. 그 결과 feature transformation과 nonlinear activation이 NGCF의 효과에 기여하지 않는다는 것을 발견했고, 더 나아가서 오히려 이것들을 제거했더니 상당한 성능 향상으로 이어진다는 점도 발견했다. 그래서 NGCF에서 사용한 feature transformation, nonlinear activation, neighborhood aggregation 중에서 GCN에 가장 필수적인 neighborhood aggregation만을 사용하여 LightGCN 모델을 만든다.

2 PRELIMINARIES

아래 식은 NGCF 모델의 수식이다 (자세한 것은 NGCF 논문 참고).
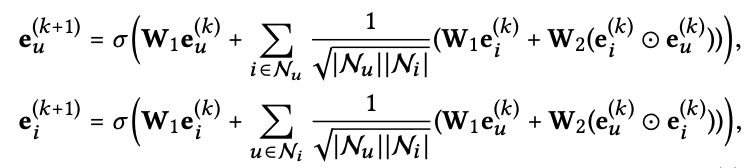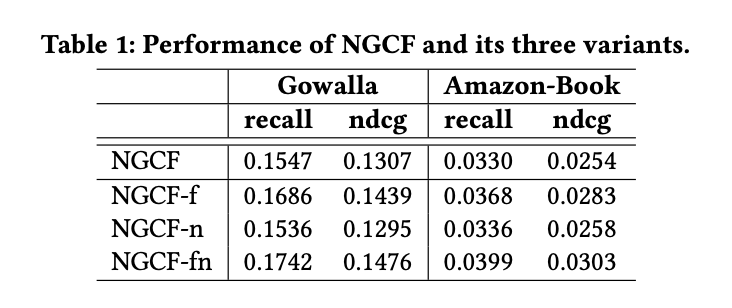
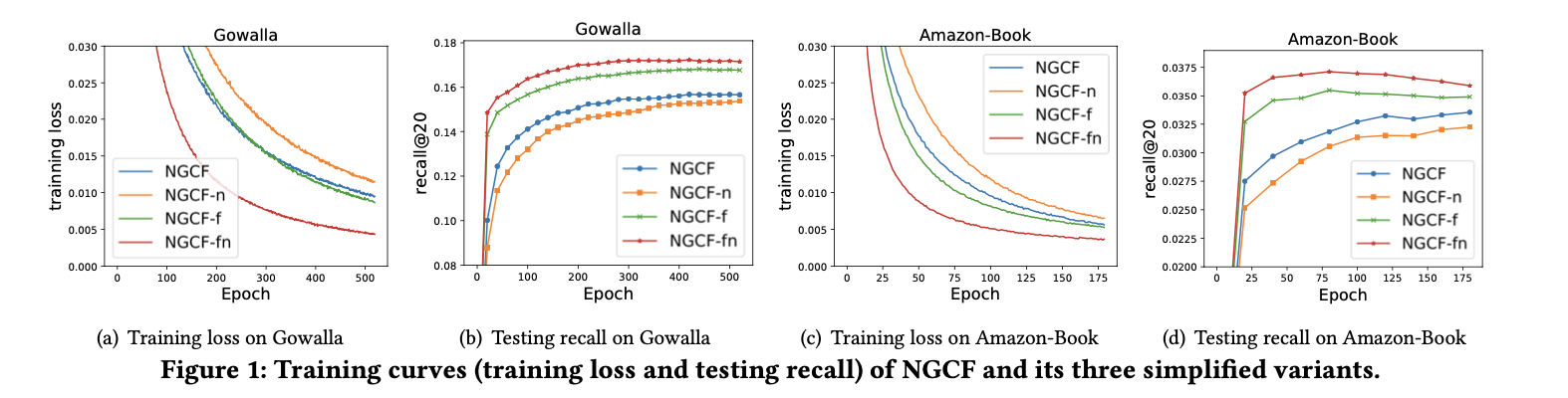
이제부터 왜 NGCF의 ablation studies를 시작한다. 아래 Figure와 Table로 설명한다.
NGCF: 오리지널 NGCF
NGCF-f: NGCF에서 feature transformation matrices W1, W2 제거
NGCF-n: NGCF에서 non-linear activation function σ 제거
NGCF-fn: NGCF에서 feature transformation matrices W1, W2 제거 + non-linear activation function σ 제거
결론적으로 NGCF-fn의 성능이 제일 높게 나오면서 NGCF에서 feature transformation matrices W1, W2 제거 + non-linear activation function σ 제거하는 것이 가장 적합한 방법이었다.
(개인적으로 느낀 것은 보통 기존 모델에서 +alpha 해서 성능을 올리는데 여기서는 기존 모델에서의 내용을 삭제하여 성능을 올렸다. ablation study가 얼마나 중요한지를 강하게 느끼게되었다)

3 METHOD

Light Graph Convolution

먼저 GCN의 AGG (aggregation fuction)을 소개한다 (위에 2 PRELIMINARIES에서 나오는 NGCF 수식을 보면 알겠지만 엄청나게 light해졌다). 여기서 앞에 붙는 symmetric normalization term은 graph convolution 작업으로 증가하는 embeddings의 scale를 피할 수 있게해준다. 여기서 눈여겨 보아야할 점은 self-connection이 없다는 것이다. 보통 aggregation을 하면 주변정보 + 자기정보를 통합하는데, 여기서는 주변정보만 가져오고 자기 자신의 정보는 가져오지 않는 수식을 보인다. 주변사람보다는 자기 자신이 본인을 가장 잘 안다. 그래서 자기 정보까지 가져와서 통합하는 것이 중요한데 이런 수식을 사용하는 이유는 뒤에서 설명된다 (결론만 먼저 말하면 이 수식이 자신의 정보까지 통합하지 않는 것 같지만 실제로는 알아서 자신의 정보를 통합한다).

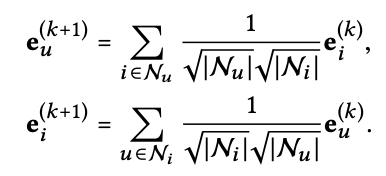
Layer Combination and Model Prediction

Light Graph Convolution을 거친 후에 최종 embedding을 구한다. 아래의 수식과 같다. 여기서 αk가 눈에 띈다. αk = 1/(k+1)로 표현된다. 이 의미는 가까운 hop에 대하여 가중치를 더 준다는 것으로 해석할 수 있다.

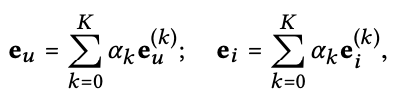
이렇게 구한 최종 embedding을 통해 prediction 값 y^ui를 inner product로 구할 수 있다.

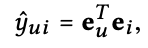
Matrix Form

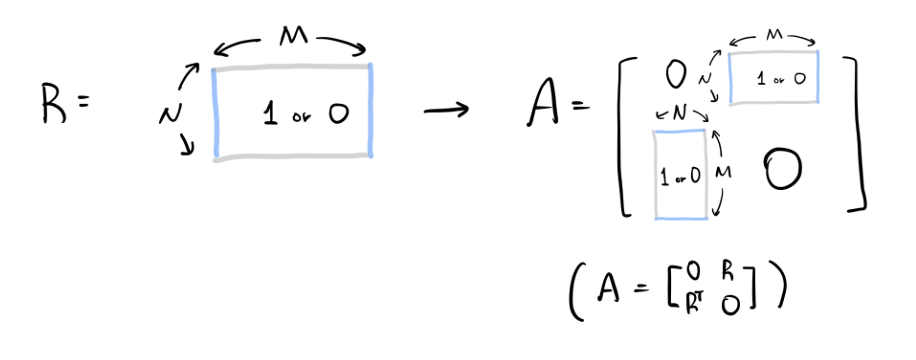
언급 안 하고 가도 될만큼 당연한 내용인데, 아주 오래전에 이제 막 추천시스템 graph 관련하여 공부를 시작할적에 이해가 안 갔던 부분이 있어 여기서 굳이 설명하려고 한다. 아래 adjacency matrix에서 user 개수가 M, item 개수가 N이라고 할 때 왜 shape가 M x N이 아니라 (M+N) x (M+N)인지 이해가 가지 않았다. 아래 있는 그림을 봤다면 이해가 빨랐을텐데 하는 아쉬움이 있다. 여기서는 user-item간의 상호작용만 있지, user-user 또는 item-item 간의 상호작용이 없기 때문에 A 행렬에서 왼쪽 위와 오른쪽 아래에 0이 생기는 것이다. 그리고 R과 RT가 각자의 자리에 들어가면서 (M+N) x (M+N)의 shape이 되는 것이다. (출처: https://wikidocs.net/176711)

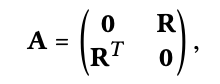
이제 아까 Light Graph Convolution section에서 언급한 수식을 matrix로 나타낸다. 식은 아래와 같다. 여기서 그 유명한 D^(-1/2) A D^(1/2)가 symmetrically normalized matrix이다. NGCF에서 이것을 contribute와 discount factor로 해석하기도 한다. contribute는 예를들어 user가 엄청 많은 item을 평가하면 해당 값은 작아지고, user가 엄청 적게 item을 평가하면 해당 값은 커지면서 가치가 있다는 것이다. 또 discount factor는 hop이 길어지면 그만큼 공헌도를 떨어트려야한다는 것이다. 어쨋든 아래와 같이 수식을 통해 embedding을 행렬 연산으로 한꺼번에 업데이트한다. 여기서 E는 (M+N) x T 차원이다. 여기서 T는 embedding size이다.

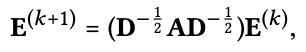
이렇게 되면 아래 수식처럼 final embedding matrix를 구할 수 있다.

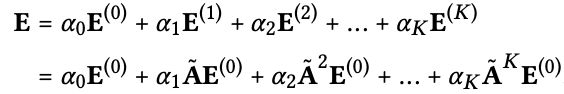
Relation with SGCN

여기서부터는 아까 Light Graph Convolution section에서 self-connection이 왜 없어도 되는지 수식적으로 설명한다. 아래는 SGCN (Simplifying Graph Convolutional Networks)의 수식이다. 여기서는 identity matrix I를 더해서 self-connection을 유지했다.여기서 상수값인 (D+I)^(-1/2)을 생략하고 수식을 풀면 아래와 같은 식이 나온다. 이 수식과 matrix form section의 마지막 수식 (final embedding matrix)을 비교하면 alpha 값만 잘 맞춰주면 form이 똑같다는 것을 확인할 수 있다. 결론적으로 LightGCN에서 self-connection 수식이 없다고 해서 실제로 self-connection이 안 되는 것이 아니라 알아서 self-connection이 되고 있으니 걱정할 필요가 없다는 것이다.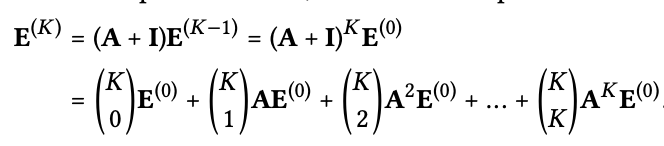

Relation with APPNP

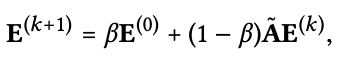
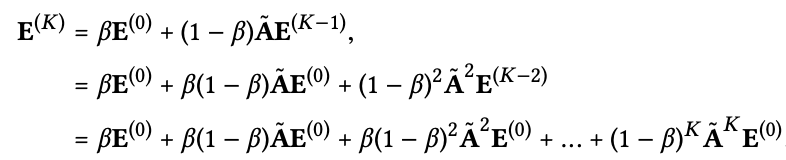
Second-Order Embedding Smoothness

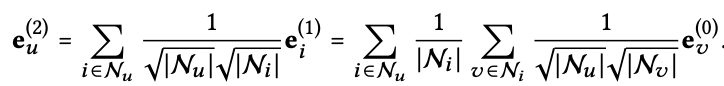
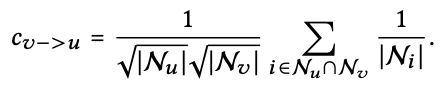
Model Training

이제 training을 하는데 이때 loss는 아래 수식인 Bayesian Personalized Ranking (BPR) loss를 사용한다. 너무 유명한 loss이니 따로 설명을 더 하지는 않겠다. 여기서 저자들은 advanced negative sampling 방법이 있다는 것을 알고는 있지만 이 논문의 초점이 여기에 맞춰져 있지 않기 때문에 이부분은 건드리지 않았다고 언급한다. 추가로 layer combination coefficients αk를 1/(k+1)로 두지 않고 직접 학습하여 설정하는 것을 수행해보았지만 성능 향상은 이끌지 못했다고 한다.

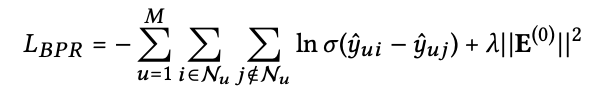
4 EXPERIMENTS

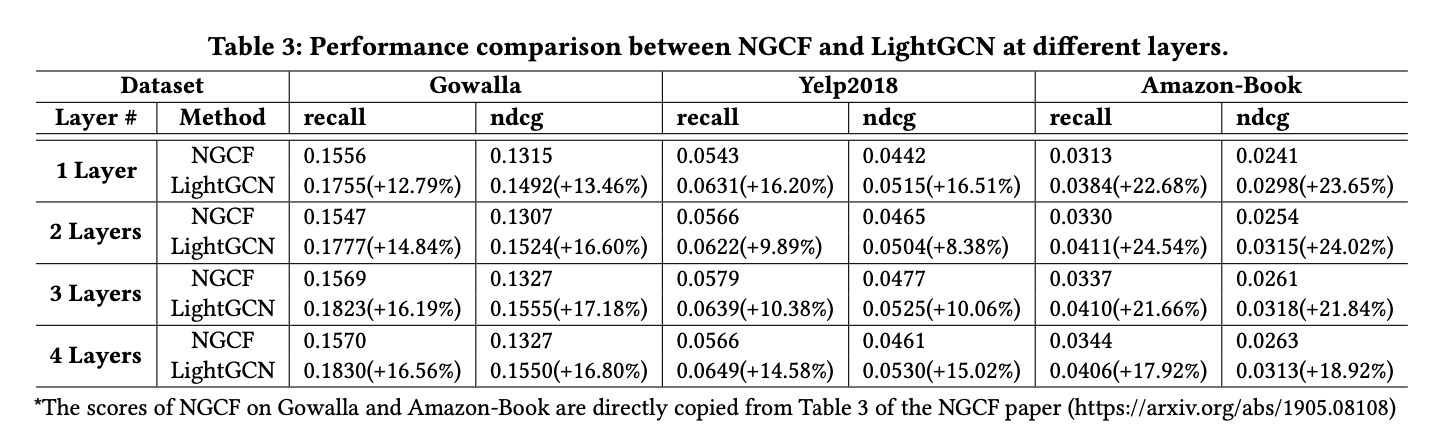
아래 결과 외에도 다양한 실험들을 많이 했고, 좋은 내용들이 많이 들어가 있으니 논문을 자세히 읽어보길 바란다.

5 RELATED WORK

• Collaborative Filtering
• Graph Methods for Recommendation

6 CONCLUSION AND FUTURE WORK

feature transformation과 nonlinear activation을 제거한 LightGCN을 소개했다. layer combination에서 final embedding을 weighted sum으로 구성하고, self-connection이 알아서 되는 것으로 입증되었고 oversmoothing을 control하는데 도움이 된다.

code

TensorFlow: https://github.com/kuandeng/LightGCN
PyTorch: https://github.com/gusye1234/pytorch- light- gcn