Review

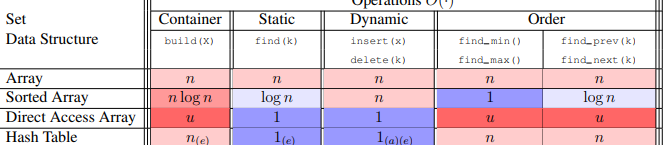
이전까지 배운 Array, Linked List, Dynamic Array, Hash Table 등 특정 함수에서 매우 뛰어난 효율을 보여줬지만 다른 함수에서는 그렇지 않았다.
그래서 이번엔 대부분의 함수에서 효율적인 걸 해보려고 한다.

Binary Tree

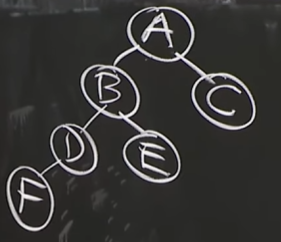
linked list 처럼 연결되어있는 형태지만 조금 다르다.

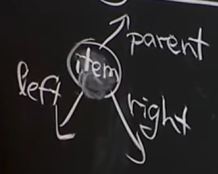
상위 노드가 있고 left, right children이 있는 형태

linked list의 경우 앞뒤를 찾는건 뛰어난 성능을 보이지만 특정 위치를 찾는건 n번 순회해야할 수 있다.
그러나 binary tree의 경우 어떤 위치에 있든 2개의 children으로 나뉘기 때문에 log n으로 찾을 수 있다.

용어

SubTree

• 해당 트리에서 특정 노드를 root node로 하는 트리를 말한다.
  • 위 사진에서 SubTree(b)면 b 아래의 모든 노드들을 포함한 트리

Depth

• number of ancestors
  • root에서 x로 가기위한 경로의 edge의 수

Edge

• node를 잇는 선

Height

• 아래에서 위로 측정함.
• x부터 가장 아래있는 리프노드 까지의 거리.
  - 가장 아래있는 리프노드란, 해당 노드가 리프 노드가 여러개 가지고 있을 수 있지만 그 중 가장 아래 있는 것을 말한다.
• 리프노드는 height가 0이다. (아래 아무것도 가지고 있지 않기 때문에)
• x의 subtree의 depth중 가장 큰값이라고 생각해도 된다.

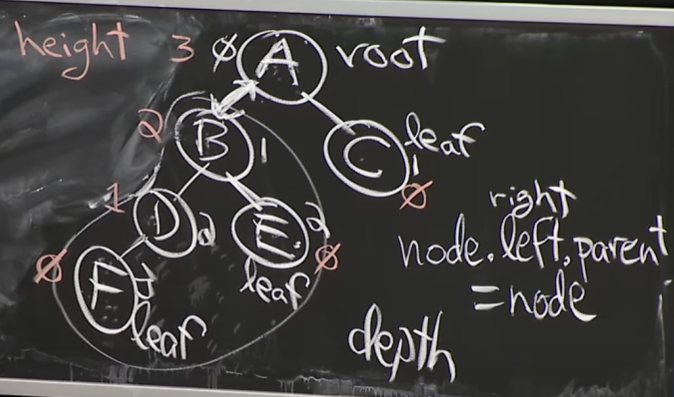
Traversal Order

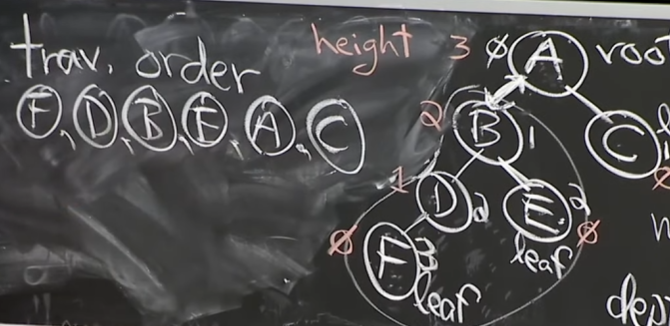
Root인 A를 기준으로 왼쪽에 있는 F,D,B,E는 왼쪽에, C는 오른쪽에 있는다.

• node x의 왼쪽 tree에 속하는 모든 노드는 x보다 먼저오고, 오른쪽 tree에 속하는 모든 노드는 x보다 나중에 온다.

iter(x):
  iter(x.left)
  output(x)
  iter(x.right)

• 항상 가장 왼쪽에 있는 leaf node가 처음으로 온다.

subtree first(node)

• go left children (until none)
• return node
• node가 더이상 나오지 않을때까지 (leaf node를 찾을때 까지) left children을 찾는다.

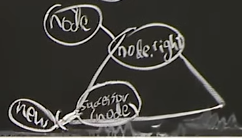
successor(node)

• O(h)
• next after node in tree's traversal order
• 오른쪽 child가 있다면 오른쪽 child의 subtree first가 successor가 된다.
  = successor(node) == subtreeFirst(node.right)
• 오른쪽 child가 없다면 successor는 node의 subtree에 없다.
  • 그러면 tree를 타고 올라가서 해당 노드가 부모의 왼쪽자식일때, 부모노드가 successor가 된다.

subtree-insert-after(node.new)

• O(h)
• 특정 노드 뒤에 새로운 노드를 넣으려고 할때
  • right child가 없으면 그냥 넣는다.
  • right child가 있으면 right child의 left child로 넣는다. (successor of node.left)
    

subtree-delete(node)

• delete하는 node가 leaf node면 그냥 parent node의 포인터를 제거하면 된다.
• leaf node가 아니라면
  • node.left가 있다면
    • node.item과 predeccesor.item을 바꾼다.
    • leaf 노드가 될때까지 바꾸고 leaf node가 되면 제거한다.
  • node.right가 있다면
    • successor와 바꾼다
    • leaf 노드가 될때까지 바꾸고 leaf node가 되면 제거한다.
• leaf node가 아니라면 제거했을때 구조가 변경될 수 있어서 실제로 삭제되는건 노드 데이터며 해당 노드 객체는 재사용된다.