Hashing

• 앞선 강의에서 find(k)는 O(log n)이 가장 효율적이었는데 더 빨리는 안되나?

comparison model

• item을 식별하는 방법은 키를 비교하는 것이 유일하다.
• = < > >= <= != 등으로 비교하는것이 다임.
• true or false로만 나타난다.

Decision Tree

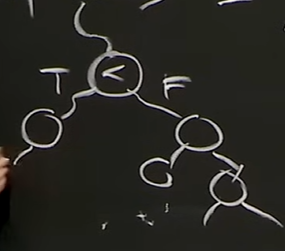
• root에서 leaves까지 비교를함

• binary tree
  - n+1만큼 leaves가 있다.
  

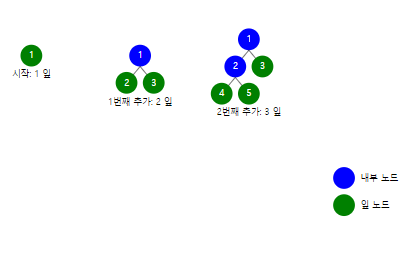
• 그렇다면 얼마나 비교해야되나?

  • 가장 긴 루트 - 리프 경로만큼

• min height

  • θ(log n)
  • 각 레벨마다 노드 수가 2배씩 증가하나 height는 1만 증가함 -> height와 노드 수에는 로그관계가 성립됨
    • 그렇기 때문에 n개의 노드로 만들 수 있는 가장 효율적인 높이는 log n임

-> 그렇다면 한번에, O(1)로 찾기위한 방법은 무엇일까?

=== Key가 10인 항목을 배열을 유지하고 index 9에 저장한다.

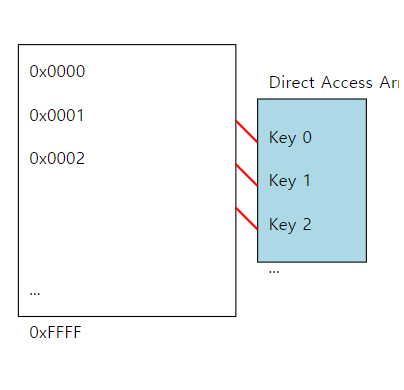
Direct Access Array

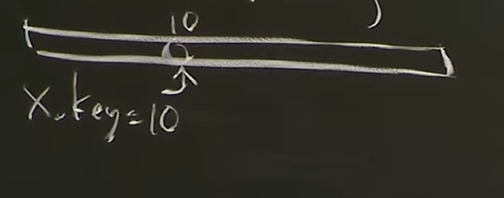
• key가 10인 것은 array의 10번째 공간에 넣어둔다.
  -> key가 10인 아이템을 찾을 때 find, insert, delete 모두 constant tiem O(1)임.
• 항상 쓸 수 없는 이유
  • 만약 id같은게 9-digit-number인 경우 300명 밖에 안되도 10^9승의 공간이 필요하다.
  • 가장 큰 key 값이 저장하고자 하는 item의 개수보다 클 때 매우 비효율 적이다.
    
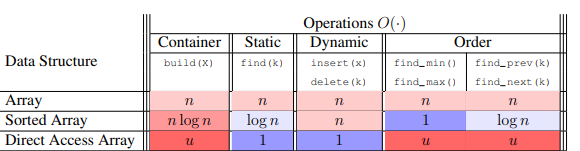
• u는 가장 큰 key 값
  (integer key)
• u < 2^w 의 조건에서 가장 효율적일 수 있다.
  • w비트로 2^w개의 고유 메모리 주소를 표현할 수 있어 모든 가능한 키를 고유한 메모리 주소에 직접 매핑하고 접근 가능하게 한다.

hashing

• 그러나 direct access array의 경우 u > 2^w면 메모리가 부족해짐
  -> 그렇다면 u의 길이를 memory의 길이만큼 줄여줄 어떤 function이 필요함
  -> 그러면 같은 index location에 1개 이상 저장해야함.

HOW?

Open Addressing

• 충돌이 일어날때 마다 다른 비어있는 공간에 넣는다
• 근데 분석하기 어려움

Chaining

• 충돌하는 key를 다른 자료구조에 저장한다.
  
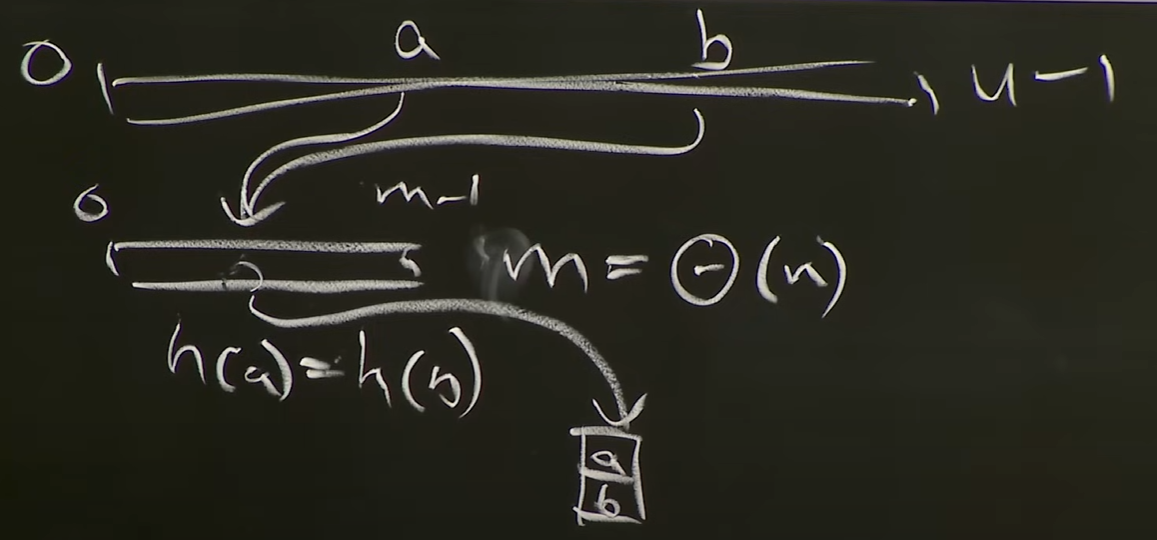
• 기존 메모리에서는 새로운 자료구조를 가리키는 포인터 역할을 한다.
• chain이 작아야 한다.
  • 새로운 자료구조를 탐색해야하기때문에 chain이 비정상적으로 길어지면 O(n)이 될 수있다.
    • 모든 버킷이 같은 키에 해시되는 경우
• 그러나 고르게 분포된다면 체인은 상수로 취급되므로 O(1)이라고 볼 수 있다.

Hash Functions

division hash function

h(k) = k mod m

• 가장 쉬운 방법
• h(k) 는 해시값
• k는 해시할 키
• m은 해시 테이블의 크기
• ex)
  key: 234
  m: 10
  해시값: 234 % 10 -> 4
• m이 중요하다.
  • m이 소수여야한다. 만약 2의 거듭제곱이면 하위 비트만 사용하여 해시 품질이 떨어진다.
• key 값 역시 중요한데 패턴이 있는 key값이라면 한 공간에 전부 chaining 되는 경우가 생길 수 있다.

Universal hash function

h(x) = ((ax + b) mod p) mod m

• x는 해시할 키
• a와 b는 0 < a < p, 0 ≤ b < p 범위의 무작위 정수
• p는 x보다 큰 소수
• m은 해시 테이블의 크기

• 위 division hash function의 문제인 해시값의 균일한 분포를 보장하기 위해 설계된 함수다.
• 단일 해시 함수의 경우 특정한 입력 집합에 대해 나쁜 성능을 보이게 되는데 이를 극복하기 위해 고안되었다.
• 해시함수 집합이 있고 이 집합에서 무작위로 해시 함수를 골라 해싱을 한다.