실험 통계학 요약 [1장 확률 이론]

이찬·2023년 6월 10일

Bayes Theorem 통계학

실험통계학 & 응용통계학

목록 보기

1/6

1. 확률 이론

1.1 확률 probabilities

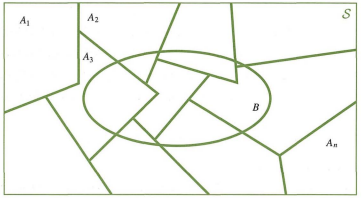
sample sapce : 표본 공간 S

결과들의 집합은 표본 공간 혹은 사상 공간이라 불리운다.

확률값
특정한 실험 결과가 나올 가능성 혹은 확률은 그 표본공간의 각 요소에 대한 일련의 확률값을 부여함으로써 구할 수 있다. 표본 공간에서의 각 결과는 0과 1사이의 확률값을 갖게 되면 표본 공간 내 요소들의 확률 총합은 1이 되어야만 한다.

기회 게임에서 모든 실험 결관느 동일한 가능성 하에 발생하는 것으로 간주되며, 따라서 그 확률값이 같다. 같은 표본 공간에서 n개의 결과가 나온다면 개개의 확률은 1/n이 된다.

1.2 사건 Event

사건 A는 sample space S의 부분집합이다.
complement 여사건

1.3 사건의 조합

교집합 Intersections of Events
P(A n B) + P(A n B') = P(A)

Mutually Exclusive Events
공통의 결과가 없는 두 사건 A와 B : 상호배반사건

Unions of Events
사건 A와 B가 상호 배반일 때 P(A n B) = 0이 되며,
P(A U B) = P(A n B') + P(A' n B) + P(A n B)
= p(A) + p(B)

Combinations of Three or More Events

표본공간의 분할은 모든 사건의 합이 S인 상호배반사건의 집합이다.

1.4 조건부 확률 Conditional Probability

사건 b가 발생했다는 조건 하에 사건 A가 발생할 조건부 확률

1.5 사건들의 교집합 확률 Probabilities of Event Intersections

General Multiplication Law

조건부 확률을 통해 교집합을 구한다.

=> 사건 A와 b 모두 발생할 확률은 사건 B가 발생할 확률과 사건 B가 발생했다는 조건하에 사건 A가 발생할 조건부 확률을 곱함으로써 구할 수 있다.

-Independent Events

두 사건이 상호 독립이라는 의미는 한 사건에 대한 정보가 나머지 다른 사건의 확률에 영향을 주지 않음을 나타낸다.

1.6 사후 확률

- Law of Total Probability 전확률의 법칙
S = A1 U ... U An

일련의 사건 Ai가 발생한다고 할 때 또 다른 사건 B의 조건부 확률 P(B|Ai)의 가중 평균으로부터 구할 수 있다. 이 경우 가중치는 P(Ai)가 된다.

- Bayes’s Theorem 베이즈 정리

P(A) : 사전 확률
P(A|B) : 사후 확률
베이즈 정리는 사전 확률과 사후 확률의 관계에 대해 설명하고 있음
베이즈 정리(Bayes' theorem). 어떤 사건이 서로 배반하는 원인 둘에 의해 일어난다고 할 때 실제 사건이 일어났을 때 이것이 두 원인 중 하나일 확률을 구하는 정리를 베이즈의 정리라고 한다.

베이즈 정리를 이해하기 어려웠던 이유

확률에 대한 관점의 변화가 필요
전통적인 관점 : 빈도주의 => 100번 동전을 던졌을 때 50번은 앞면이 나온다.
새로운 관점 : 베이지안 주의 => 확률을 주장에 대한 신뢰도로 해석하는 관점 => 동전의 앞면이 나왔다는 주장의 신회도가 50%이다.

- 확률론 패러다임의 전환 : 연역적 추론에서 귀납적 추론

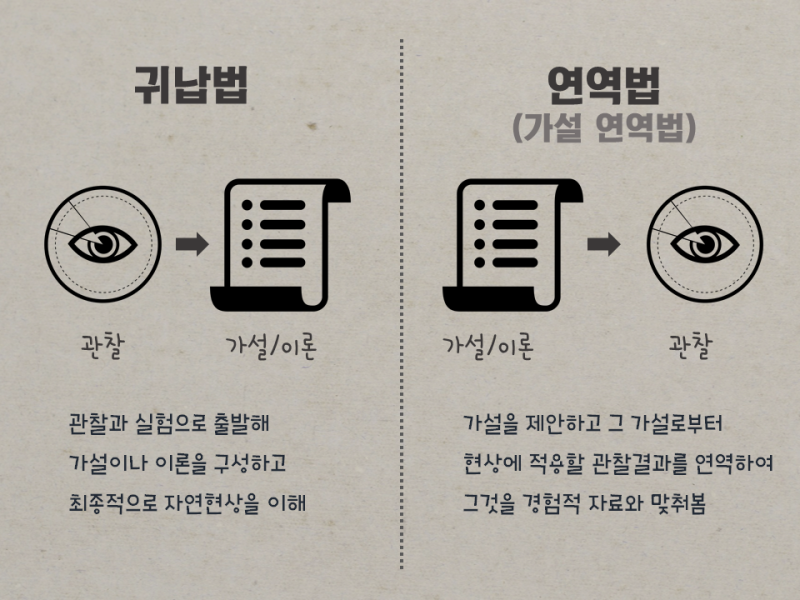
연역추리에서는 전제가 참이면 결론도 필연적으로 참인데 비해, 귀납추리에서는 전제가 참이어도 참이 보증되진 않습니다. 예를 들어 백조는 희다는 관찰이 꾸준히 있었어도, 단 하나의 검은 백조에 의해 반박됩니다.

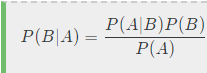
결국 조건부 확률(사후 확률)을 구하는 것을 말하는데, 이는 어떤 사건이 만들어 놓은 상황에서, 그 사건이 일어난 후 앞으로 일어나게 될 다른 사건의 가능성을 구하는 것을 말한다. 즉, 기존 사건들의 확률(사전 확률)을 알고 있다면, 어떤 사건 이후의 각 원인들의 조건부 확률을 알 수 있다는 것이다. 하지만 기존 사건들의 확률을 알지 못한다면 베이즈 정리는 쓸모없는 것이 되는 한계가 있다. 대부분의 사회 통계는 전수조사가 불가능하기에 기존 사건들의 확률 역시 알 수 없는 것이어서 한 때 베이즈 정리는 관심 밖에 있었으나, 최근 빅 데이터를 통해 기존 사건들의 확률을 대략적으로 뽑아낼 수 있게 됨으로써(데이터가 쌓일수록 확률의 정확도는 올라간다.), 사회적 통계나 주식에서의 빅 데이터를 이용한 베이즈 정리 활용이 필수적인 것으로 되고 있다.

-베이즈 정리의 의의와 머신러닝과의 연관성
이처럼 베이즈 정리를 이용할 경우 , 관찰결과를 토대로 사후 확률(주장의 신뢰도의 정도)를 지속적으로 업데이트 해나갈 수 있습니다. 우리가 마주치는 머신러닝 문제들도 어떤 가설을 설정하고 데이터(=관찰 결과)를 토대로 가설을 지속적으로 업데이트 해나가는 과정이기 때문에 많은 부분에 베이즈 정리를 적용할 수 있고 베이즈 정리에 기반한 기법들이 광범위하게 사용되고 있습니다. 따라서 머신러닝 전문가가 되기 위해서는 베이즈 정리에 대한 제대로된 이해가 필수적입니다.