Paper : Variable Bitrate Neural Fields

Abstract

배경

• 부호 있는 거리 함수 및 복사 필드와 같은 스칼라 및 벡터 필드의 신경 근사치는 정확한 고품질 표현으로 나타났습니다. 훈련 가능한 특징 그리드로부터의 조회를 통해 신경 근사치를 조절함으로써 최첨단 결과를 얻을 수 있습니다[Liu et al. 2020; Martelet al. 2021; Mülleret al. 2022; Takikawaet al. 2021] 학습 작업의 일부를 담당하고 더 작고 효율적인 신경망을 허용합니다. 불행하게도 이러한 기능 그리드는 일반적으로 독립형 신경망 모델에 비해 메모리 소비가 크게 증가하는 대가를 치르게 됩니다.

제안

• 우리는 이러한 특징 그리드를 압축하고, 메모리 소비를 최대 100배까지 줄이고, 코어 외부 스트리밍에 유용할 수 있는 다중 해상도 표현을 허용하는 사전 방법을 제시
• 우리는 직접적인 감독이 불가능한 공간과 동적 토폴로지 및 구조를 사용하여 종단 간 이산 신경 표현을 학습할 수 있는 벡터 양자화 자동 디코더 문제로 사전 최적화를 공식화

결과

• https://github.com/nv-tlabs/vqad

3 BACKGROUND

논문 전체에서 사용되는 용어와 개념에 대한 개요를 제공하기 위해 신호 압축 및 신경장에 대한 배경 지식을 제공한다.

좌표 $x$를 값에 매핑하는 연속 함수로 신호 $u(x) : \mathbb R → \mathbb R$를 정의한다. 이산 신호 처리에서 신호는 일반적으로 길이 $n$의 시퀀스 값으로 근사되며, 연속 신호의 균등한 간격 샘플을 나타낸다:

• $u_i$ : 시퀀스의 $i$ 번째 샘플

연속 신호 $u(x)$가 bandlimited되어 있고 샘플 $u_x$의 간격이 Nyquist rate를 초과하는 경우, 연속 신호는 sinc interpolation을 사용하여 정확하게 재구성될 수 있다.

Nyquist rate
주어진 함수 또는 신호의 가장 높은 주파수(대역폭)의 두 배에 해당하는 값

sinc interpolation(Whittaker–Shannon interpolation formula)
실수 시퀀스로부터 연속적인 시간 bandlimited 함수를 구성하는 방법

컴퓨터 그래픽은 좌표가 2차원, 3차원 또는 그 이상이고 출력 차원이 $d > 1$인 다차원, 다중 채널 신호를 처리하는 경우가 많다. 다차원 축은 종종 1D로 평면화되고 채널은 별도의 신호로 처리될 수 있다.

neural field [Xie et al. 2021]는 stochastic optimization를 통해 맞춰진 매개변수 $θ$를 갖는 연속 함수로, 연속 신호를 근사화하는 매개변수 함수 $ψ_θ (x) \approx u(x)$이다. NeRF를 포함하는 대중적인(global) 방법의 매개변수는 전적으로 MLP의 가중치와 편향으로 구성된다.

반대로, Feature-grid 방법은 feature-grid 매개변수 $Z$로 MLP를 강화한다. feature-grid는 일반적으로 규칙적인 간격의 그리드이며 함수 interp는 주어진 좌표 $x$에 대해 local feature vector $z = \text{interp}(x,Z)$를 보간하는 데 사용된다.

$ψ_θ (x,\text{interp}(x,Z)) \approx u(x)$는 비선형 함수이므로 이 접근 방식은 일반적인 Nyquist limit을 초과하는 주파수로 신호를 재구성할 가능성이 있다. 따라서 더 거친 그리드를 사용하여 신호 압축에 사용하는 방향을 고려할 수 있다.

Nyquist frequency
연속 함수 또는 신호를 이산 시퀀스로 변환하는 샘플러의 특성
Nyquist limit
색상 또는 펄스파 초음파에서 앨리어싱을 초래하지 않고 정확하게 측정할 수 있는 최대 도플러 편이 주파수

Feature grid는 행렬 $Z ∈ \mathbb R^{m×k}$로 표현될 수 있다. ($m$은 그리드 점의 개수, $k$는 각 그리드 점에서의 feature vector의 차원) $m×k$는 MLP의 크기에 비해 클 수 있으므로 feature vector는 메모리를 가장 많이 소모하는 구성 요소이다. 따라서 feature grid를 압축하고 이산 신호 압축을 찾고자 한다.

예를 들어, Instant-NGP [Müller et al. 2022] 는 10,000개의 MLP 가중치와 1,260만 개의 feature grid 매개변수를 활용하여 radiance field를 나타낸다.

Transform coding

이산 신호를 압축하는 표준 방법으로 transform coding을 사용할 수 있으며, 이 함수는 이산 신호 $u_x$를 표현 $v_x$로 변환한다.

• 변환된 표현 $v_x$ : transform coefficients

이 변환의 역할은 계수에 양자화(quantization) 또는 절단(truncation)을 적용하여 효과적으로 압축할 수 있도록 신호를 역상관(decorrelate)시키는 것이다.

Linear transform coding

선형 변환 $A ∈ \mathbb R^{n×n}$을 사용하여 변환 계수 $v_x = Au_x$를 생성한다. 신호 $u_x$는 역 $A^{−1}$ 로 재구성될 수 있다. 이러한 변환 행렬은 고정되거나(DFT 및 DCT와 같은 효율적인 변환을 기반으로 함) 데이터로 구성될 수 있다.

예를 들어 KLT(Karhunen-Loève transform)는 가우스 분산 데이터를 최적으로 역상관시킬 수 있는 데이터 기반 변환이다.

Non-linear transform coding

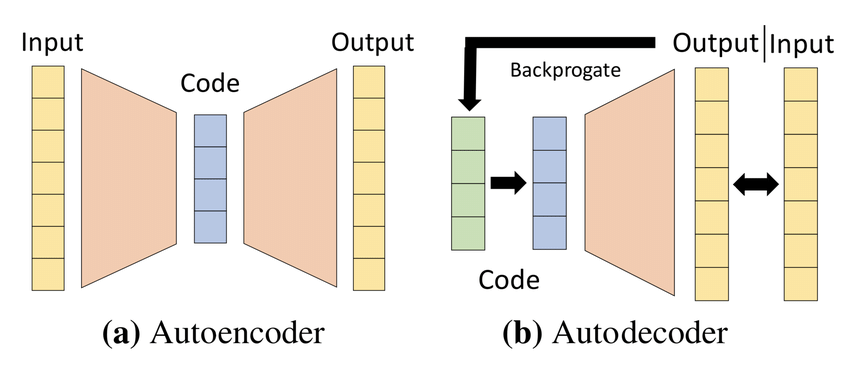
이산 신호를 인코딩하고 디코딩하기 위해 inverse $f^{−1}_\gamma$와 함께 매개변수 $\gamma$로 구성된 parametric function $f_\gamma: \mathbb R^n → \mathbb R^n$을 사용한다. (변환 $f_\gamma$는 신경망일 수 있다) 비선형 변환 코딩은 '변환 계수들을 압축'하는 추가적인 목적을 가지고 있으며, auto-encoder로 알려진 것과 유사한 구성을 가지고 있다.

한편, auto-decoder는 inverse transform $f^{−1}_\gamma$ 를 명시적(explicit)으로 정의하고 변환 매개변수 $\gamma$ 및 변환 계수 $v_x$ 에 대한 stochastic optimization를 통해 forward transform을 수행하는 것만을 나타낸다. 즉, forward transform은 $f(u_x) = \argmax_{v_x, \gamma},\| f^{−1}_\gamma(v_x) − u_x \|$이다. 이는 stochastic variational inference의 한 형태로 볼 수도 있다. auto-encoder의 비선형 변환 코딩과 유사하게 compressed auto-decoder 를 auto-decoder와 압축 등가물(compressive equivalent)로 정의한다.

Vector Quantization

대규모 시퀀스의 경우 전체 시퀀스의 변환을 계산하는 것은 비용이 많이 들 수 있다. Block-based 변환 코딩은 신호 $u_x$를 $k$의 고정 크기 청크로 나눈다. 큰 $n × n$ 행렬을 사용하여 global transform coefficient $v_x = Au_x$를 계산하는 대신, $u_x ∈ \mathbb R^n$ 을 행렬 $U ∈ R^{\frac{n}k ×k}$로 재구성할 수 있다. block transform coefficient를 얻기 위해 더 작은 block-wise transform $\hat A∈ \mathbb R^{ k×k}$ 가 적용된다.

비선형의 경우 $f_\gamma: \mathbb R^k → \mathbb R^k$ 함수를 사용하여 개별 블록(행렬 $U$의 행)을 코딩할 수 있다. 추가 압축을 위해 $U$의 행은 벡터 양자화를 통해 클러스터링될 수 있다. 또한 블록 기반 압축, 특히 벡터 양자화에서 영감을 얻은 방법을 사용하여 feature-grid를 압축한다.

4 METHOD

본 연구는 압축 표현 학습에 중점을 두고 auto-decoder 프레임워크를 사용하는 vector-quantized auto-decoder 방법을 제안한다. 핵심 아이디어는 부피가 큰 feature vector를 학습된 codebook의 index로 대체하는 것이다. 이러한 index, codebook 및 디코더 MLP 네트워크는 모두 공동으로 훈련된다.

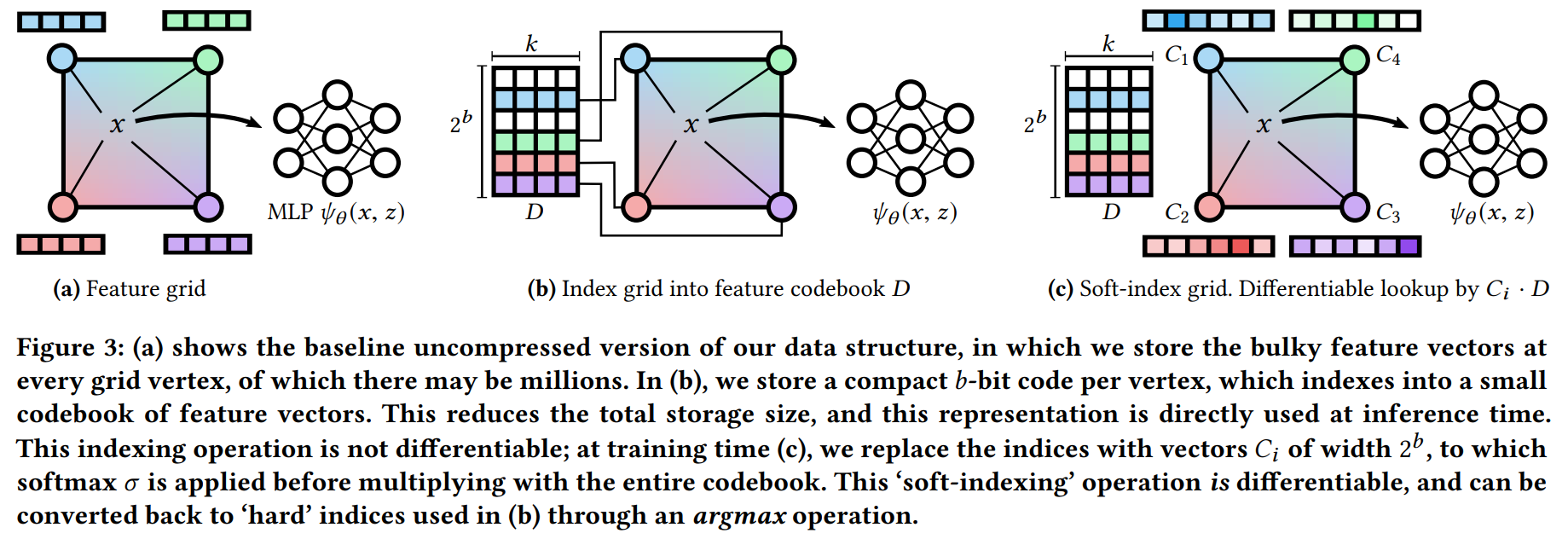
변환 코딩에 일반적으로 사용되는 인코더 함수를 피함으로써 간접 감독 하에서도 coordinate network MLP가 인코딩하는 연속 신호와 같은 임의 도메인에 대한 압축된 표현을 학습할 수 있다. 이는 볼륨 렌더러로 이미지에서 NeRF를 훈련하는 것과 같은 결과를 도출한다.

• 섹션 4.1 | 압축된 auto-decoder 프레임워크에 대한 개요
• 섹션 4.2 | feature-grid 압축이 프레임워크에 어떻게 적합한지 보여줌
• 섹션 4.3 | 이 프레임워크의 구체적인 구현에 대한 논의

4.1 Compressed Auto-decoder

이산 신호 압축을 feature-grid에 효과적으로 적용하기 위해 디코더 $f^{-1}_\gamma$ 만 명시적으로 구성된 auto-decoder 프레임워크를 활용한다. 순방향 변환을 수행하려면 stochastic gradient descent를 통해 다음과 같은 최적화 문제를 해결해야 한다:

auto-decoder의 장점은 재구성하려는 신호와 다른 영역에서 감독과 관련하여 변환 계수를 재구성할 수 있다는 것이다. 미분 가능한 forward map을 다른 도메인으로 신호를 올리는 연산자 $F$로 정의한다. 이제 다음 문제를 해결해야 한다:

• $F$ : 미분 가능한 렌더러
• Radiance field 재구성의 경우 관심 신호 $u_x$는 체적 밀도 및 plenoptic 색상이고 감독은 2D 이미지이다.

4.2 Feature-Grid Compression

feature grid는 행렬 $Z ∈ \mathbb R^{m×k}$이다($m$은 그리드의 크기, k는 feature vector 차원). Local embedding은 좌표 $x$에서 보간을 사용하여 feature grid에서 쿼리되고 MLP $ψ$에 공급되어 연속 신호를 재구성한다. feature grid는 다음 방정식을 최적화하여 학습된다:

• interp : $x$를 둘러싼 8개 feature grid 점의 trilinear interpolation
• forward map $F$는 MLP $ψ$의 출력에 적용(본 실험에서는 미분 가능한 렌더러)
• $y$ : 훈련 이미지 픽셀

Feature grid $Z$는 크기 $k$의 각 행 vector(block)가 로컬 공간 영역을 제어하는 신호의 블록 기반 분해로 처리될 수 있다. 따라서 본 연구는 블록 계수 $V$를 사용하여 block-based inverse transforms $f^{-1}_\gamma$ 를 고려한다. 압축된 feature $Z = f^{-1}_\gamma (V )$ 를 학습하기 위해 $Z$를 다음과 같이 대체한다:

$F(\psi (x,\theta,\text{interp}(x,Z)))$ 를 이산 신호 $Z$를 감독(및 다른 작업)이 적용된 연속 신호로 올리는 맵으로 간주하면 이는 block-based compressed auto-decoder와 동일하다는 것을 알 수 있다. 이를 통해 이산 신호 $Z$로만 작업하여 feature-grid $Z$에 대한 압축 inverse transform $f^{-1}_\gamma$ 를 설계할 수 있으며, 본 연구의 경우 vector-quantized inverse transform을 통해 압축 표현을 직접 학습할 수 있다.

4.3 Vector-Quantization

벡터 양자화가 압축된 자동 디코더 프레임워크에 어떻게 통합될 수 있는지 보여줍니다.

Index grid into feature codebook D

압축된 표현 $V$는 $[0, 2^b −1]$ 범위의 정수 벡터 $V ∈ \mathbb Z^m$으로 정의한다. 이는 코드북 행렬 $D ∈ \mathbb R^{2^b × k}$에 대한 인덱스로 사용된다($m$은 그리드 포인트의 수, $k$는 feature vector 차원, b는 bitwidth). 구체적으로, 디코더 함수 $f^{−1}_D (V ) = D[V ]$를 정의한다([·]는 인덱싱 작업).

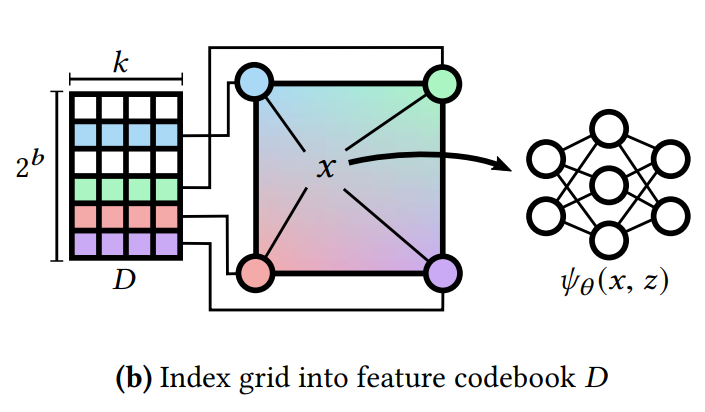
최적화 문제는 다음과 같다:

Soft-index grid

인덱싱은 정수 인덱스 $V$에 대해 미분 불가능한 연산이기 때문에 이 최적화 문제를 해결하는 것은 어렵다. 이를 해결하기 위해 훈련 중 row-wise argmax에서 인덱스 벡터 $V = \argmax_i C[i]$를 얻을 수 있는 softened matrix $C ∈ \mathbb R^{m×2^b}$로 정수 인덱스를 나타내는 것을 제안한다. 그런 다음 인덱스 탐색을 간단한 행렬 곱으로 대체하고 다음과 같은 최적화 문제를 얻을 수 있다.

• softmax 함수 $σ$는 행렬 $C$에 row-wise로 적용
• 이 최적화 문제는 이제 미분 가능!

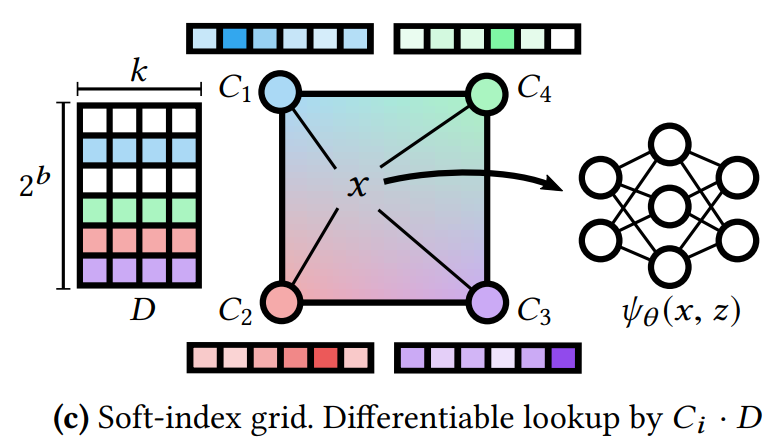
훈련 중에 손실이 하드 인덱싱을 인식하도록 하는 접근 방식인 실제로 우리는 직선 추정기를 채택한다. 즉, 순방향 패스에는 식 8을 사용하고 역방향 패스에는 식 9를 사용한다.

저장 및 추론 시, 연화된 행렬 C를 버리고 정수 벡터 V만 저장합니다. 엔트로피 코딩 없이도 이는 16mk/(mb + k2 b )의 압축 비율을 제공하며, 이는 b가 작고 m이 클 때 크기가 수십 배일 수 있다. 우리는 일반적으로 m이 수백만 단위인 것을 관찰하고 실험을 위해 b ∈ {4, 6}을 평가한다. 해시 함수를 사용하는 것과 대조적으로 인덱싱을 위해서는 b비트 정수를 특징 그리드에 저장해야 하지만 인덱스의 학습된 적응성으로 인해 훨씬 ​​더 작은 코드북(테이블)을 사용할 수 있습니다.

단일 해상도 피처 그리드 대신 NGLOD에서와 같이 다중 해상도 희소 옥트리에 V를 배열합니다[Takikawa et al. 2021], 스트리밍 세부 수준을 촉진합니다. 따라서 주어진 좌표에 대해 여러 특징 벡터 z가 얻어집니다(각 트리 레벨에서 하나씩). 그런 다음 MLP로 전달되기 전에 합산되거나(즉, 라플라시안 피라미드 방식으로) 연결될 수 있습니다. 우리는 트리의 각 수준에 대해 별도의 코드북을 훈련합니다. NGLOD와 유사하게 [Takikawa et al. 2021], 우리는 또한 여러 수준의 세부 사항을 공동으로 훈련합니다.