Paper : Local-to-Global Registration for Bundle-Adjusting Neural Radiance Fields

Abstract

배경

• NeRF(Neural Radiance Fields)는 사실적인 새로운 뷰 합성을 달성했으나 정확한 카메라 포즈에 대한 요구 사항으로 인해 적용이 제한됨
• 신경 3D 표현을 공동으로 학습하고 카메라 프레임을 등록하기 위한 합성별 분석 확장이 존재함에도 불구하고 제대로 초기화되지 않으면 차선책에 취약

제안

• 번들 조정 Neural Radiance Fields를 위한 로컬-투-글로벌 등록 방법인 L2G-NeRF를 제안
• 픽셀 단위의 유연한 정렬과 프레임 단위의 제한된 파라메트릭 정렬이 이어짐
• 픽셀별 로컬 정렬은 광도 재구성 오류를 최적화하는 심층 네트워크를 통해 감독되지 않는 방식으로 학습
• 프레임별 전역 정렬은 전역 변환을 찾기 위해 픽셀별 대응에 대해 미분 가능한 매개변수 추정 솔버를 사용하여 수행됩니다.

결과

• 합성 및 실제 데이터에 대한 실험을 통해 우리의 방법이 충실도가 높은 재구성 및 대형 카메라 자세 오정렬 해결 측면에서 현재의 최첨단 방법보다 성능이 우수하다는 것을 보여줌

3. Approach

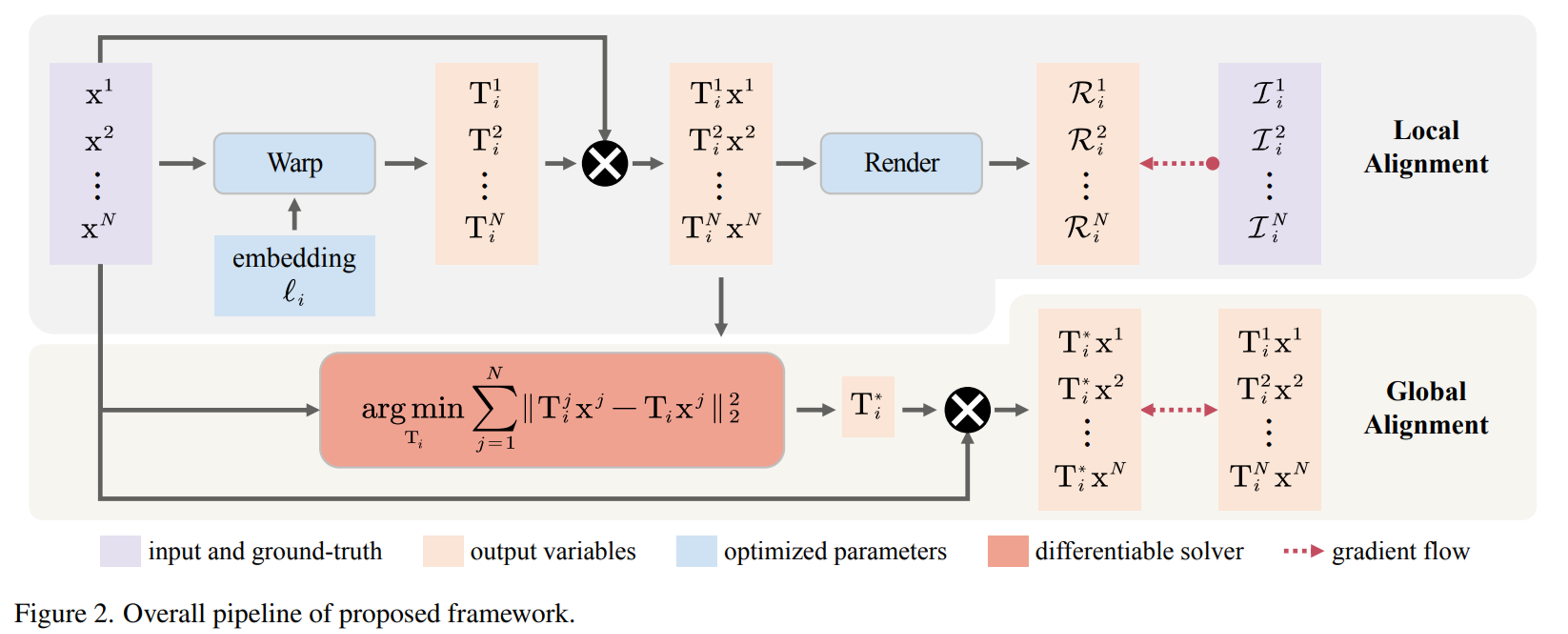
카메라 매개변수와 함께 neural field를 재구성하는 공식을 제시한다. 이미지 세트 $\{\mathcal I_i\}^M_{i=1}$이 주어지면 우리는 neural field $\mathcal R$의 매개변수 $Θ$와 렌더링된 이미지와 실제 이미지 사이의 photometric error를 최소화하는 카메라 매개변수 $\{\mathbf T_i\}^M_{i=1}$을 공동으로 찾는 것을 목표로 한다. 샘플링된 좌표 $\{\mathbf x^j\}^N_{j=1}$ 에 대한 이미징 함수를 다음과 같이 공식화한다:

Gradient-based optimization은 최적이 아닌 카메라 포즈를 찾는 경향이 있다. 따라서 본 논문은 local-to-global registration을 위한 전략을 제안한다. 핵심 아이디어는 photometric reconstruction error를 픽셀별 유연한 정렬을 적용하여 개별적으로 최적화한 다음, 식 1을 확장하여 local geometric transformation을 global로 제한하는 프레임별 정렬을 적용하는 것이다:

• $\{\mathbf T_i^j\}^{M,N}_{i=1,j=1}$ : pixel-wise local transformation으로, frame-dependent embedding $\{ℓ_i\}^M_{i=1}$과 함께 $Φ$로 매개변수화된 warp neural field $\mathcal W$에 의해 모델링
  $\mathbf T_i^j = \mathcal W(\mathbf x^j;ℓ_i, \Phi), \tag 3$

$\{T^*_i\}^M_{i=1}$ 은 픽셀별 대응(pixel-wise correspondences)에 대해 미분 가능한 매개변수 추정 솔버를 사용하여 추정한다:

3.1. Neural Image Alignment (2D)

직관적으로 문제를 정의하기 위해 먼저 2차원에서의 이미지 정렬 문제를 가정해보자. $\mathbf x ∈ \mathbb R^2$ 를 2D 픽셀 좌표로 하고 $\mathcal I : \mathbb R^2 → \mathbb R^3$ 이라고 하면 가중치 $Θ$로 매개변수화된 MLP $f_{\mathcal R} : \mathbb R^2 → \mathbb R^3$ 2D neural field를 최적화하는 것을 목표로 한다.

• $\mathbf T = \mathbf{[R|t]} ∈$ SE(2) 또는 $\mathbf T ∈$ SL(3)과 같은 geometric transformation parameters
  를 해결
• $\mathbf R ∈$ SO(2) 및 $\mathbf t ∈ \mathbb R^2$ : rigid rotation and translation
• $\mathbf T ∈$ SL(3) : 각각의 homography transformation matrix

가중치 $\Phi$로 매개변수화된 다른 MLP를 사용하여 frame-dependent embedding $ℓ$에서 coordinate-based warp neural field $f_{\mathcal W}: \mathbb R^2 → \mathbb R^3$ 조건을 모델링한다:

• exp(·) : Lie algebra $se(2)$ 또는 $sl(3)$에서 Lie group SE(2) 또는 SL(3)까지의 지수 맵을 나타내며, 이는 gradient-based optimization 동안 최적화된 변환 행렬 $\mathbf T$가 Lie group manifold에 놓이도록 함

3.2. Bundle-Adjusting Neural Radiance Fields (3D)

3D NeRF(Neural Radiance Fields)와 카메라 포즈를 동시에 추정하는 문제에 대해 논의한다. 3D 점이 주어지면 네트워크 매개변수를 사용하여 3D 장면을 인코딩하는 MLP $f_{\mathcal R} :\mathbb R^3 →\mathbb R^4$를 통해 RGB 색상 $\mathbf c ∈ \mathbb R^3$ 및 볼륨 밀도 $σ ∈ \mathbb R$을 예측한다.

이는 카메라 뷰 공간에서 NeRF의 렌더링 프로세스를 공식화하는 것부터 시작한다. 픽셀 좌표 $\mathbf u ∈ \mathbb R^2$ 의 homogeneous 좌표는 $\mathbf x = [\mathbf u; 1]^⊤ ∈ \mathbb R^3$로, 깊이 $z_i$에서 ray위의 3D 점은 $z_i\mathbf x$로 표현될 수 있다. 따라서 query quantity는 $\mathbf y = [\mathbf c; σ]^⊤ = f_{\mathcal R}(z_i\mathbf x; Θ)$이며, 여기서 $Θ$는 $f_{\mathcal R}$의 매개변수이다. 그런 다음 픽셀 위치 $\mathbf x$의 렌더링 색상 $\mathcal R$은 볼륨 렌더링으로 계산할 수 있다

• $T(\mathbf x, z) = \exp (− \int^{z}_{z_{\text{near}}} σ(z^′\mathbf x)dz^′)$
• $z_{\text{far}}$ 및 $z_{\text{far}}$ : 장면의 근거리 및 원거리 깊이 경계

수치적으로 적분 공식은 깊이 $\{z_1, ..., z_K\}$의 ray 위의 샘플링된 $K$개의 점을 사용하여 이산적으로 근사된다. 네트워크 $f_{\mathcal R}$은 $K$번 평가되고, 출력 $\{y_1, ..., y_K\}$는 볼륨 렌더링을 통해 합성된다. $\mathcal R(\mathbf x)$이 $g(\mathbf y_1, ..., \mathbf y_K)$로 표현될 수 있도록 미분 가능하고 결정론적인 합성 함수를 $g: \mathbb R^{4K} → \mathbb R^3$으로 표시한다.

카메라 포즈는 $\mathbf T = [\mathbf R|\mathbf t] ∈$ SE(3) ($\mathbf R ∈$ SO(3) 및 $\mathbf t ∈ \mathbb R^3$)로 매개변수화된다. 다음으로, 3D rigid transformation $\mathbf T$를 사용하여 3D 점 $z_i\mathbf x$를 카메라 뷰 공간에서 세계 좌표로 변환하고 픽셀 $\mathbf x$의 렌더링 색상을 다음과 같이 공식화한다:

Neural 이미지 정렬과 유사하게 가중치 $Φ$를 갖는 또 다른 MLP를 사용하여 frame-dependent embedding $ℓ$과 함께 coordinate-based warp neural field $f_{\mathcal W} : \mathbb R^2 → \mathbb R^6$를 모델링한다.

• exp(·) : Lie algebra $se(3)$에서 Lie group SE(3)까지의 지수 맵

IDK

3.3. Differentiable Parameter Estimation