Paper : Robust Camera Pose Refinement for Multi-Resolution Hash Encoding

3. Method

multi-resolution hash encoding을 사용한 카메라 포즈 개선을 위한 naïve error back-propagation가 sinusoidal(정현파) 인코딩을 사용하는 것에 비해 좋지 않은 결과를 보임을 관찰했다.

• 관찰 내용을 더 자세히 이해하기 위해 multi-resolution hash encoding의 파생을 분석(섹션 3.1)
• multi-resolution hash encoding의 gradient fluctuation으로 인해 포즈 개선과 장면 재구성을 공동으로 학습하기가 어렵다는 점 지적(섹션 3.2)
• 이러한 문제를 해결하기 위해 multi-resolution hash encoding에서 부정확한 카메라 포즈를 보정하는 방법 제안(섹션 3.3)
• 장면의 multi-level decomposition이 multi-level encoding의 서로 다른 수렴 속도를 유도하여 카메라 포즈 registration이 제한된다는 것 발견(섹션 3.4)

3.1

3.1.1

vanila Multi-Resolution Hash Encoding of Instant NGP

3.1.2. DERIVATIVE OF MULTI-RESOLUTION HASH ENCODING

Gradient 분석을 위해 $\mathbf x$에 대한 multi-resolution hash encoding의 파생을 도출한다.

• $\mathbf c_{i,l}(\mathbf x)$ : $\mathbf x_l$이 위치한 레벨 $l$ 해상도 그리드의 코너 $i$
• $h_l(·)$ : $l$-level에 대한 hash function
• $\mathcal H=\{\mathcal H_l|l \in \{1,...,L\}\}$ : feature table

출력이 $2^d$ 모서리를 가진 $l$번째 보간된 feature vector인 $\mathbf h_l: \mathbb R^d → \mathbb R^F$ 함수를 고려한다:

• $w_{i,l}$ : $d$-선형 가중치를 나타내며, 상대 위치 $\mathbf x$가 다음과 같은 unit hypercube의 반대 volume으로 정의:
  $w_{i,l}=\prod^d_{j=1}(1-|\mathbf x_l-\mathbf c_{i,l}|_j) \tag 5$
• index j : 벡터의 j번째 차원

Multi-resolution hash encoding vector $\mathbf y$를 재정의한다:

• $F' = L × F$ : concatenation 후 출력 벡터의 차원

$\mathbf x$에 대한 $l$번째 보간된 feature vector $\mathbf h_l(\mathbf x)$의 Jacobian $∇_{\mathbf x}\mathbf h_l(\mathbf x) \in \mathbb R^{F\times d}$는 다음과 같이 chain-rule을 사용하여 유도될 수 있다.

• $mathcal H_l(h_l(\mathbf c_{i,l}(\mathbf x)))$ : $\mathbf x$에 대해 미분 가능하지 않음

$\nabla_\mathbf x w_{i,l} ∈ \mathbb R^{1×d}$의 $k$ 번째 요소는 다음과 같이 정의된다.

• $s_k$ = $sign(\mathbf c_{i,l}(\mathbf x)-\mathbf x)_k$

식 (7)에서 볼 수 있듯이 Jacobian $∇_{\mathbf x}\mathbf h_l(\mathbf x)$는 $\mathbf x$의 가까운 모서리에 해당하는 hash table 항목의 가중 합이다. 그러나 gradient $∇_{\mathbf x_k} w_{i,l}$ 은 변수 $s_k$로 인해 모서리에서 연속적이지 않아 gradient 방향이 반전된다. 이러한 gradient $∇_{\mathbf x} w_{i,l}$ 의 진동(발진)은 $\mathcal H$와 별개로 gradient fluctuation의 원인이다.

gradient fluctuation
학습 중에 모델 파라미터에 대한 gradient 값이 불안정하게 변하는 현상

3.2

However, they have limited performance compared to multiresolution hash encoding

3.3. Non-linear Interpolation for Smooth Gradient

Gradient fluctuation을 완화하기 위해 straight-through estimator의 forwarding pass를 유지하는 interpolation weight $w_{i,l} ∈ [0, 1]$에 대해 smooth gradient의 사용을 제안한다. Smooth gradient를 위해 hypercube의 모서리에서 도함수가 0인 activation function δ(wi,l)와 wi,l ∈ [0, 1]을 사용한다:

• $w_{i,l}$ : activation value [0,1]

결과적으로 $\mathbf x$에 대한 $w_{i,l}$의 기울기는 다음과 같이 도출된다:

• $\nabla_\mathbf x \delta(w_{i,l})$ : 연속적이지 않으며 hypercube의 경계를 통해 뒤집힘
• sine 함수에 의한 가중치는 효과적으로 gradient를 부드럽고 연속적으로 만듦(그림 2(b))
  
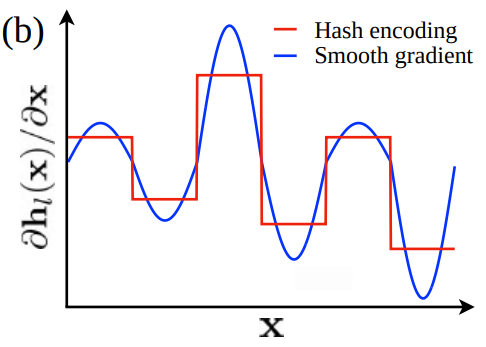
• 경계 근처의 $\mathbf x$의 gradient는 그리드 중앙에 비해 상대적으로 줄어들므로 카메라 포즈 업데이트 후 경계를 가로질러 자주 앞뒤로 이동하는 것을 방지할 수 있음

그러나 interpolation forward pass에서는 이를 직접 사용하지 않는다. 식 (11)의 cosine 함수는 샘플링된 점을 그리드 가장자리를 향해 선으로 의도치 않게 분산시킨다. 이는 “zigzag 문제"라고 부르며 특정 hypercube에서 smooth interpolation을 직접 사용하면 샘플링된 점이 가장자리에 가까워진다.

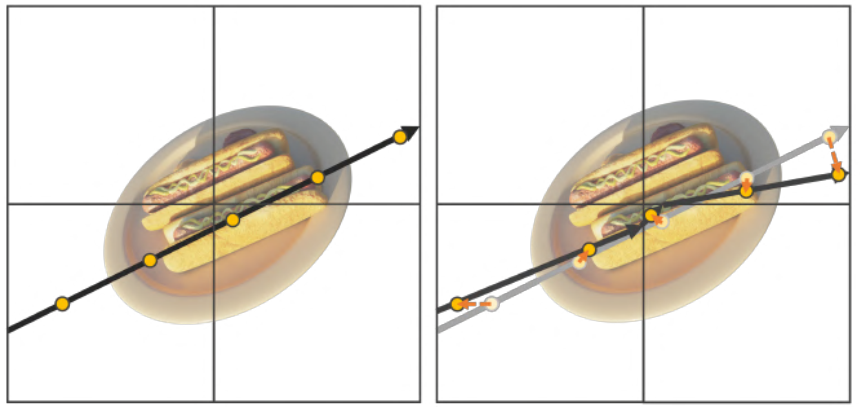
이 현상은 straight-through estimator로 해결할 수 있다:

• 마지막 두 항을 cancel-out하여 forward pass에서 선형 보간 결과를 유지하고, backward pass에서 activation value $δ(w_{i,l})$을 부분적으로 사용
• $λ$ : smooth gradient와 zigzag 문제를 조정하는 하이퍼파라미터
• $\tilde \delta$ : 계산 그래프에서 분리된 변수

Hash encoding $\mathbf h$의 gradient fluctuation(흔들리는 빨간색 화살표)을 약화시키기 위해 gradient smoothing (a) → (b) 을 활용한다. 카메라 포즈 개선을 위해 error back-propagation pass는 $d$-선형 보간 가중치 $w$를 통과한다. 그러나 그 파생물은 hash grid 모서리에 대한 입력 좌표 $\mathbf x$의 sign of relative position에 의해 결정된다. 이로 인한 gradient fluctuation으로 인해 수렴이 어렵다.

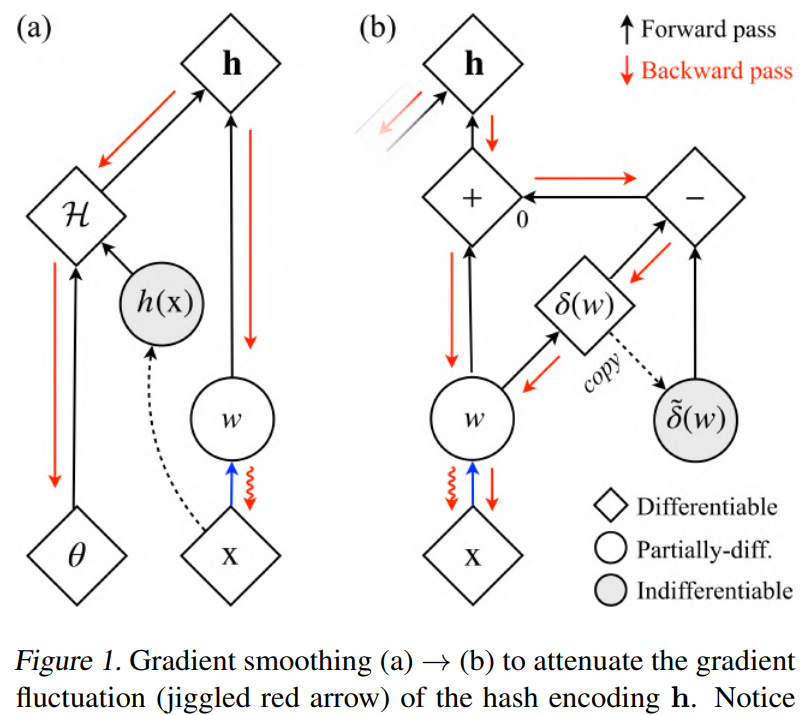
• straight-through estimator는 식 (13)의 추가로 gradient를 완벽하게 매끄럽고 연속적으로 만들지는 않지만 다른 혼합 변형보다 더 효과적
  

3.4. Curriculum Scheduling

NeRF는 계층적 구조를 나타내기에 좌표 기반 MLP는 서로 다른 주파수가 서로 다른 속도로 수렴하는 spectral bias 문제를 겪을 수 있다. BaRF는 포즈를 개선하여 이 문제를 해결한다. 연구에 따르면 k번째 위치 인코딩의 야코비언은 포즈 노이즈를 증폭시켜 위치 인코딩의 순진한 적용이 포즈 개선에 부적합하다는 것을 보여주었다. 장면의 다단계 분해를 활용하는 다중 해상도 해시 인코딩도 비슷한 문제를 나타낸다. 문제를 해결하기 위해 레벨별 인코딩의 수렴률을 조절하는 교육과정 스케줄링 전략을 제안한다. 다중 해상도 해시 인코딩의 l번째 레벨에 다음과 같이 가중치를 부여한다:

• $\alpha(t)=L \cdot \frac{t-t_s}{t_e-T_s}\in[0,L]$ : $s$는 scheduling interval $[t_s, t_e]$ 의 반복 횟수 $t$에 비례

이 가중치 함수는 Nerfies와 Barf에서 제안한 Coarse-to-Fine 방법과 유사하다. 이 방법을 사용하면 디코딩 네트워크가 모든 수준의 인코딩을 수신할 수 있는 반면, 높은 수준의 인코딩은 거친 수준보다 더 느리게 업데이트된다. 경험적으로 이 multi-level coarse-to-fine 전략이 multi-resolution hash encoding에 효과적이라는 것을 발견했다.