자료구조 개념정리 2편 - 스택, 큐, 해시 테이블

Jongma·2025년 3월 14일

글또 스택 알고리즘 자료구조 큐 해시 테이블

자료구조

목록 보기

2/2

스택 (Stack)

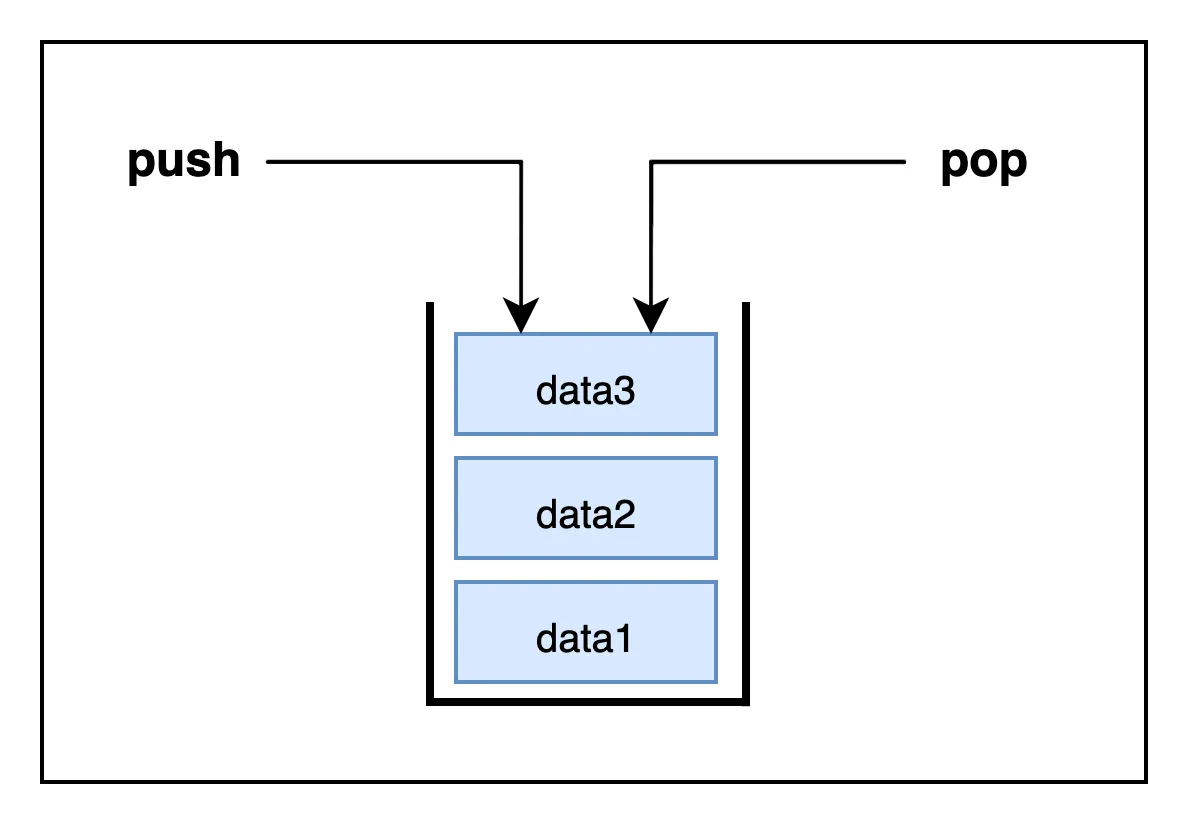
스택 자료구조는 한 쪽 끝에서만 넣고 빼기가 가능한 LIFO(Last In First Out) 형태의 자료구조이다.

예를 들어서 접시를 겹쳐서 쌓아두었는데 맨 밑의 접시를 꺼내기 위해서는 가장 마지막에 놓은 접시부터 차례대로 꺼내와야 하는데 이처럼 마지막에 집어 넣은 데이터를 처음 꺼내와야 하는 자료구조가 스택이다.

파이썬에서 스택 사용

stack = []

stack.append(1)
stack.append(2)
stack.append(3)

# [1, 2, 3]
print(stack)

# 3
print(stack.pop())

위와 같이 리스트를 사용하면 스택으로 사용할 수 있다.
append로 맨 끝에 추가하고, pop으로 맨 끝에 있는 요소를 꺼낼 수 있다.

큐 (Queue)

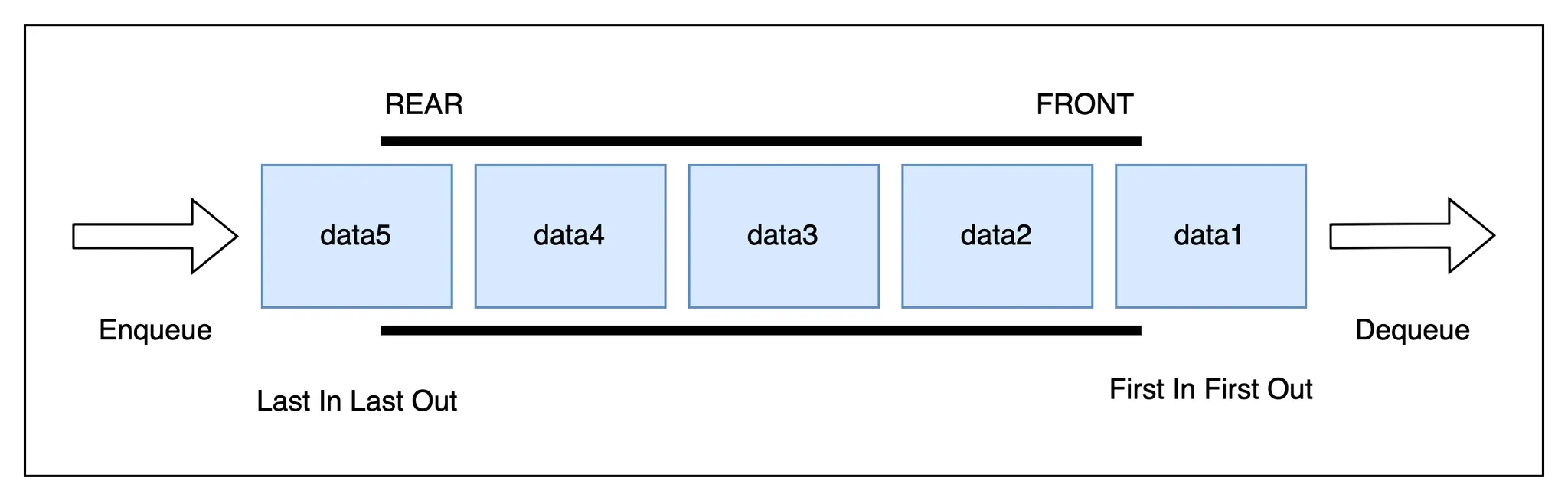
큐 자료구조는 먼저 집어 넣은 데이터가 먼저 나오는 FIFO(First In First Out) 형태의 자료구조이다.

예를 들어서 어떤 맛집에 들어가기 위해서 줄을 서고 있는데 가장 처음 먼저 줄을 선 사람이 가장 먼저 입장할 수 있다. 이처럼 가장 처음 집어 넣어진 데이터가 가장 처음 나오게 되는 자료구조가 큐이다.

파이썬에서 큐 사용

파이썬에서 리스트 자료형은 동적 배열로 구현되어 있기 때문에 스택 자료 구조로 사용하기에는 적합하지만 큐 자료구조 형으로 사용하기에는 부적합하다.

그 이유는 동적 배열은 연속된 메모리 구조를 갖고 있기 때문에 첫 번째 요소를 꺼내기 위해서는 나머지 요소들을 왼쪽으로 한 칸씩 옮겨줘야 하기 때문에 시간 복잡도가 O(N)만큼 소요되기 때문이다.

deque 활용

from collections import deque

queue = deque()

queue.append(1)
queue.append(2)
queue.append(3)

# deque([1, 2, 3])
print(queue)

# 1
print(queue.popleft())

리스트 자료형 대신 colletions 모듈의 deque을 사용하면 popleft 메소드를 통해서 시간 복잡도 O(1) 만큼을 소요하면서 첫 번째 요소를 꺼내올 수 있어서 큐 자료 구조형을 잘 사용할 수 있다.

deque의 popleft 메소드가 시간 복잡도가 O(1) 만큼 밖에 걸리지 않는 이유는 양방향 연결 리스트로 구현되어 있기 때문에 맨 앞과 끝에서 삽입 / 삭제가 수행 되더라도 포인터만 변경 해주면 되기 때문이다.

해시 테이블 (Hash Table)

해시 테이블이란?

해시 테이블은 키-값(Key-Value) 쌍을 저장하는 자료구조이다.
간단하게 설명하면 키를 입력 값으로 넣어서 해시 값을 가져옴 → 해시 값을 인덱스로 변환함 → 해당 인덱스는 배열의 인덱스로 사용 → 저장하고자 했던 값을 해당 인덱스에 삽입

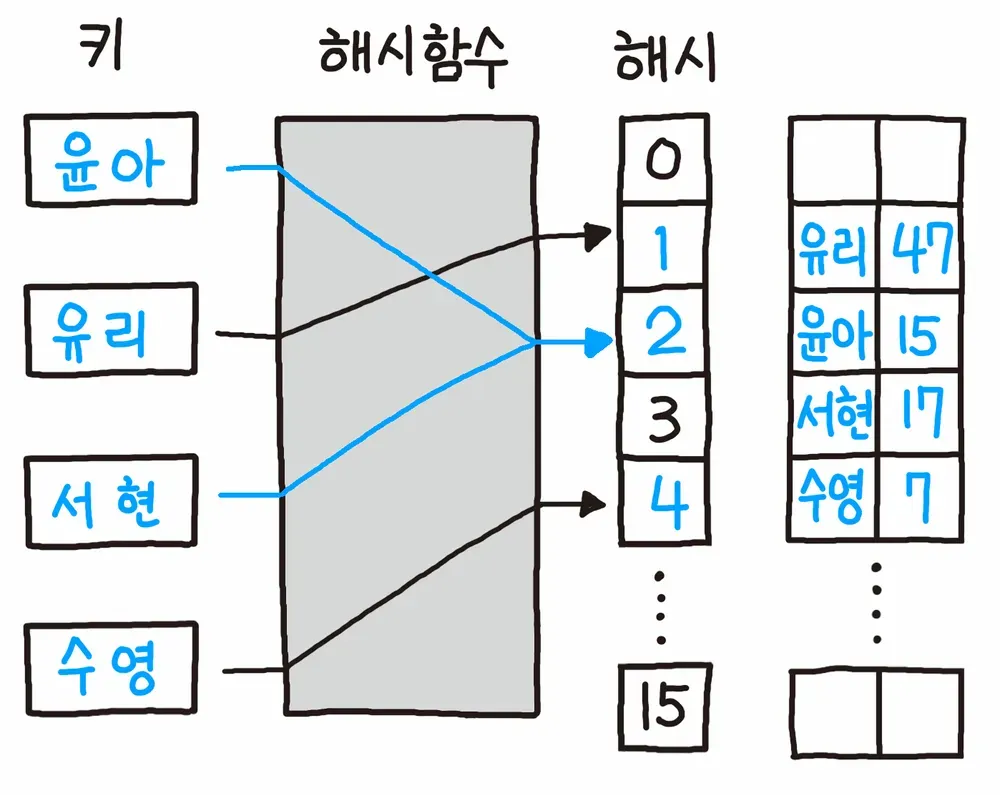
해시테이블

출처: https://namu.wiki/w/해시

위 내용만으로는 어려울 수 있으니 아래에 자세하게 풀어보았다.

‘윤아: 15’ 키-값 쌍으로 해시 테이블에 저장하고자 함
키를 해시 함수에 입력 값으로 넣어서 출력 값으로 해시 값을 계산
해시 값을 테이블의 크기 만큼 나누어서 나머지 값을 배열의 인덱스로 사용
배열에 2번 인덱스로 15라는 값을 삽입

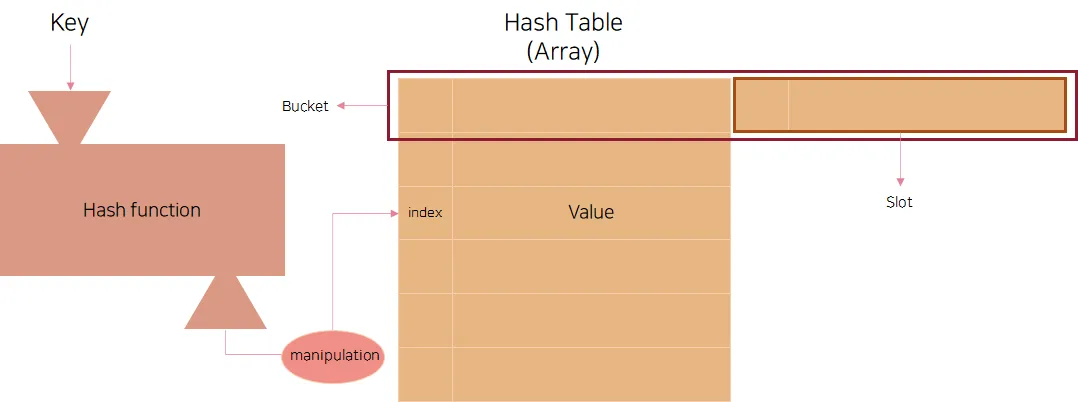
해시테이블-버킷-슬롯

출처: https://velog.io/@fore0919/TIL-자료구조-해쉬테이블Hash-Table

이때 데이터를 저장하는 배열을 테이블(Table)이라고 부르고, 테이블은 여러 개의 버킷(Bucket)을 가질 수 있고, 버킷은 여러 개의 슬롯(Slot)을 가질 수 있다. 슬롯은 키-값 한 쌍의 데이터를 저장할 수 있다.

위와 같은 순서로 키-값 구조로 데이터를 저장할 수 있다.
조회할 때도 동일하게 키를 전달하면 해시 함수를 통해서 인덱스를 얻을 수 있고
테이블에서 인덱스로 접근하기 때문에 조회 시 시간 복잡도는 O(1) 밖에 소요되지 않는다.

코드 예시

class HashTable:
    def __init__(self):
        self.table = [None] * 8

    def put(self, key, value):
        ...

    def get(self, key):
        ...

해시 테이블은 기본적으로 위와 같은 형태를 갖고있다.
그럼 위에서 설명한 순서를 코드로 풀어서 봐보자.

def put(self, key, value):
		# 키를 해시 함수에 입력 값으로 넣어서 출력 값으로 해시 값을 계산
    hash_value = hash(key)
    print(hash_value)  # 5060017407582588215

		# 3. 해시 값을 테이블의 크기 만큼 나누어서 나머지 값을 배열의 인덱스로 사용
    index = hash_value % len(self.table)
    print(index)  # 7

		# 4. 배열에 7번 인덱스로 15라는 값을 삽입
    self.table[index] = value

hash_table = HashTable()
# ‘윤아: 15’ 키-값 쌍으로 해시 테이블에 저장하고자 함
hash_table.put("윤아", 15)

hash(’윤아’) → 5060017407582588215 해시 값 획득
5060017407582588215 % len(self.table) → 7번 인덱스 획득

해시 충돌(Collision)

만약 데이터를 처리하는 양이 매우 많아진다면 해시 함수에서 얻은 해시 값도 중복이 발생할 수 있다. 이처럼 해시 값이 중복되는 상황을 해시 충돌(Collision)이라고 한다.
이러한 해시 충돌을 해결 하기 위한 대표적인 방법으로는 체이닝(Chaining)과 개방 주소법(Open Addressing)이라는 방법이 있다.

체이닝(Chaining)

기본적인 해시 테이블에서 버킷은 하나의 키-값 쌍을 저장하는 단위이다.
하지만 이 형태에서는 해시 충돌이 발생하면 값을 저장할 수 없는 문제가 있는데, 이를 해결하기 위한 방법 중 하나로 체이닝 방식이 쓰인다.
체이닝 방식은 버킷이 하나의 키-값 쌍을 저장하지 않고, 연결 리스트(Linked List), 동적 배열과 같은 자료구조들을 활용해 하나의 버킷에 여러 개의 키-값 쌍을 저장할 수 있도록 하는 방식이다.

다음과 같은 순서로 진행된다.

해시 함수를 통해 키의 해시 값을 계산하고 인덱스로 변환
인덱스로 조회해서 버킷이 비어 있으면 값을 저장
버킷이 이미 사용 중이라면 연결 리스트에 새로운 데이터를 추가

하지만 이렇게 저장할 경우 조회할 때 인덱스 접근 → 연결 리스트에서 키를 찾아서 값을 조회
순으로 접근하게 되는데 인덱스 접근은 시간 복잡도가 O(1)만 소요되지만 연결 리스트에서 키를 찾는 과정은 시간 복잡도가 O(N)이 소요되게 된다.

코드 구현

class HashTable:
    def __init__(self):
        self.table = [[] for _ in range(8)]

    def put(self, key, value):
				...

    def get(self, key):
				...

위와 같이 테이블의 버킷을 리스트(동적 배열)로 구성했다.

def put(self, key, value):
    index = hash(key) % len(self.table)
    for pair in self.table[index]:
		    # 동일한 키 값이 있을 경우 업데이트
        if key == pair[0]:
            pair[1] = value
            return

    # 인덱스가 충돌하더라도 버킷이 리스트이므로 계속 추가할 수 있어서 문제 없음
    self.table[index].append([key, value])

값의 삽입은 위와 같이 구현할 수 있다.
→ 인덱스가 충돌하더라도 버킷이 리스트라 계속 추가 가능

def get(self, key):
    index = hash(key) % len(self.table)
    # 인덱스로 버킷 접근 -> 시간 복잡도 O(1)
    for pair in self.table[index]:
		    # 동일한 키를 탐색, 있다면 반환 -> 시간 복잡도 O(N)
        if key == pair[0]:
            return pair[1]

    # 키가 없다면 None을 반환
    return None

값의 조회는 위와 같이 구현할 수 있다.
→ 인덱스로 버킷 접근 O(1) → 리스트에서 동일한 키를 탐색 O(N)

개방 주소법(Open Addressing)

해시 테이블 충돌의 두 번째 해결 방법으로는 개방 주소법을 사용한다.
개방 주소법은 해시 충돌이 발생하면 한 버킷에 여러 데이터를 저장하는 체이닝 방식과 달리, 버킷은 하나의 슬롯만 갖고 충돌하면 빈 슬롯을 탐색해서 데이터를 저장하는 방식이다.

이러한 개방 주소법의 방식은 선형 조사법(Linear Probing), 이차 탐사(Quadratic Probing), 이중 해싱(Double Hashing) 세 가지 방식이 존재한다.

모두 설명하기엔 너무 분량이 길어져서
간단하게 설명하고 기회가 있다면 별도로 다루어 보겠다.

선형 탐사

인덱스를 +1 하면서 빈 버킷을 찾는 방식
간단하게 구현할 수 있지만, 연속된 버킷이 차면 성능이 저하 (클러스터링 문제 발생)
개선하기 위해서 이차 탐사 방식 사용

이차 탐사

인덱스를 제곱 하면서 빈 버킷을 찾는 방식
테이블의 크기가 소수(primary number)가 아니라면 사용하지 않는 슬롯 존재
개선하기 위해서 이중 해싱 방식 사용

이중 해싱

첫 번째 해시에서 충돌이 일어날 경우 두 번째 해시 값도 계산해서 빈 버킷을 찾는 방식
클러스터링 문제를 최소화 할 수 있음

시간 복잡도 비교 (스택 vs 큐 vs 해시 테이블)

	조회	삽입	삭제
스택	O(N)	O(1)	O(1)
큐	O(N)	O(1)	O(1)
해시 테이블	O(1) - 평균 / O(N) - 최악	O(1) - 평균 / O(N) - 최악	O(1)O(1) - 평균 / O(N) - 최악

스택(Stack): LIFO → push()와 pop()은 O(1)소요, 조회 → 선형 탐색 필요 O(N) 소요
큐(Queue): FIFO → enqueue()와 dequeue()는 O(1) 소요, 조회 → 선형 탐색 필요 O(N) 소요
해시 테이블(Hash Table): 평균적으로 모든 연산이 O(1)이지만 해시 충돌이 많을 경우 O(N) 소요

마무리

스택, 큐, 해시 테이블에 대해서 정리해봤다.
사실 스택과 큐는 단순해서 알고 있는 내용이 대부분이었지만 해시 테이블은 실무에서 가장 많이 사용하는 자료구조 임에도 불구하고 잘 모르고 있음을 알 수 있었다.

특히 해시 충돌에 대한 내용을 잘 모르고 있어서 해시 테이블이 O(1)의 시간 복잡도를 갖는 만능의 자료구조형인 줄 알았지만 이번 기회에 해시 충돌로 인해서 O(N)이 될 수 있음을 알게 되어서 주의하게 사용할 수 있게된 것 같다.

참고

Jongma

이전 포스트