완전이진트리이다
노드를 추가할때 최하단 왼쪽 노드부터 차례대로 추가한다
최소값 최대값을 빠르게 찾기 위해 고안되었다
우선순위큐(우선순위가 높은 데이터를 먼저 꺼내는 것)를 구현할때 활용된다
이진탐색트리와 비교해보자
공통점: 이진트리
차이점
-힙은 각 노드의 값이 자식 노드보다 크거나 같음(Max Heap의경우)
-이진 탐색 트리는 왼쪽 자식노드의 값이 가장 작고, 그 다음 부모 노드, 그 다음 오른쪽 자식 노드 값이 가장 큼
-힙은 이진 탐색 트리의 조건인 자식 노드에서 작은 값은 왼쪽, 큰 값은 오른쪽이라는 조건은 없음
-이진 탐색 트리는 탐색을 위한 구조. 힙은 최대/최소값 검색을 위한 구조중 하나로 이해하면 됨
힙의 구조
힙은 최대값을 구하기 위한 구조 Max Heap
최소값을 구하기 위한 구조 Min Heap 으로 분류
힙은 다음과 같이 두 가지 조건을 가지고 있다
1. 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 크거나 같다(최대힙의경우)
최소힙의 경우 각 노드의 값은 해당 노드의 자식 노드가 가진 값 보다 작거나 같다
2. 완전 이진트리 형태를 가짐
최대힙의 경우 노드 추가시
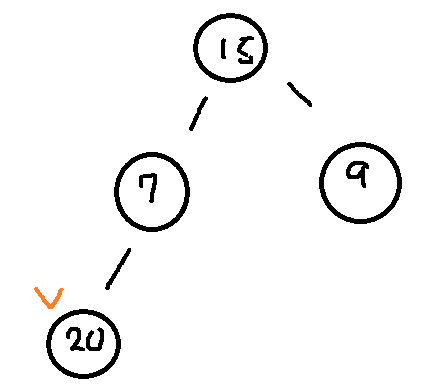
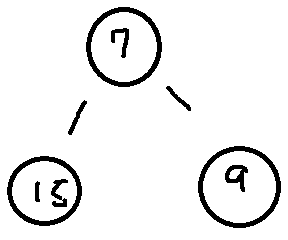
20을 추가한다고 생각해보자 일단 가장 왼쪽 말단 노드의 왼쪽에 연결한다
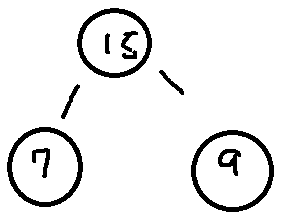
그리고 20은 부모인 7보다 큰 값이므로 7과 20의 값을 교환한다. 노드의 연결을 바꿀 필요가 없다
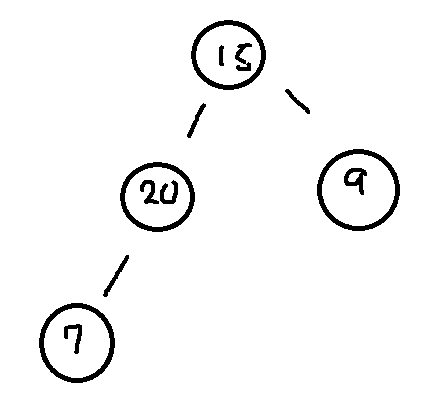
그리고 20은 15보다도 큰 값이므로 또 15와 20을 값만 바꾼다
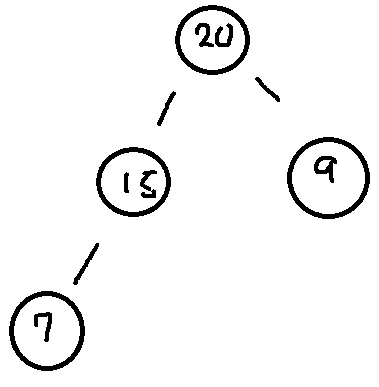
힙의 데이터 삭제하기
최대힙(Max Heap)의 예
최상단 노드만 삭제가능함
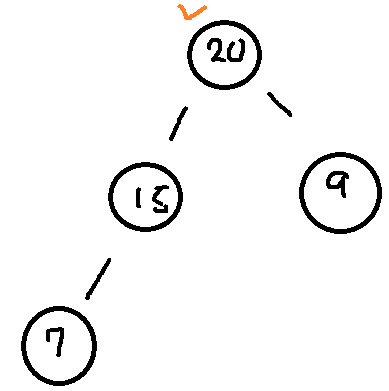
그리고 가장 하위레벨의 오른쪽 자녀를 루트노드로 올린다. 실제 구현은 최상단 노드의 값만 최하단 가장 오른쪽 자녀의 값으로 덮어씌우면 될듯하다.
그리고 바뀐 최상단 노드의 자녀들중 큰 값과 비교해서 작다면 값을 교체한다
힙의 구현
일반적으로 배열을 사용한다. 왜냐면 힙은 완전이진트리로서 루트노드부터 말단노드 가장 오른쪽 까지 번호를 매기고 그 번호를 쉽게 계산해서 찾을 수 있기 때문이다
부모노드 인덱스 번호 = 자식노드 인덱스 / 2
왼쪽자식 인덱스 번호 = 부모인덱스 x 2
오른쪽 자식 인덱스 번호 = 부모인덱스 x 2 + 1
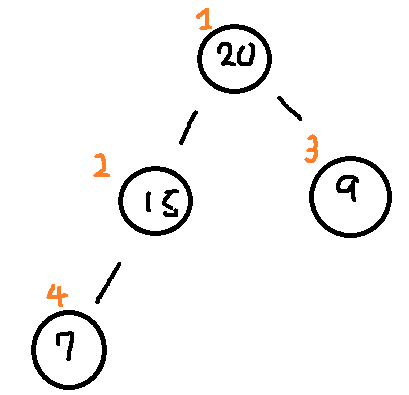
구현할때 배열의 0번 배열은 사용하지 않고 1번 배열부터 루트노드의 인덱스로 사용하면 구현하기 수월하다
ArrayList 배열을 사용해서 구현하였다
public class MyHeap {
ArrayList<Integer> list;
MyHeap()
{
list = new ArrayList<>();
list.add(0);
}
void Insert(Integer value)
{
list.add(value);
if(list.size() == 2)
return;
int curidx = list.size()-1;
int parentidx = curidx / 2;
int temp = 0;
while(curidx != 1)
{
if(list.get(parentidx) < value)
{
temp = list.get(parentidx);
list.set(parentidx, value);
list.set(curidx, temp);
curidx = parentidx;
parentidx = curidx / 2;
}
else
break;
}
}
int Pop()
{
int result = list.get(1);
int curidx = list.size()-1;
list.set(1, list.get(curidx));
list.remove(curidx);
curidx = 1;
while(true)
{
int leftchildidx = curidx * 2;
int rightchildidx = curidx * 2 + 1;
//no child
if(leftchildidx > list.size() -1)
break;
//left only child
else if(leftchildidx == list.size() -1)
{
if(list.get(curidx) < list.get(leftchildidx))
{
int temp = list.get(curidx);
list.set(curidx, list.get(leftchildidx));
list.set(leftchildidx, temp);
curidx = leftchildidx;
}
else
break;
}
//two child
else if(rightchildidx < list.size())
{
if(list.get(leftchildidx) > list.get(rightchildidx))
{
if(list.get(curidx) < list.get(leftchildidx))
{
int temp = list.get(curidx);
list.set(curidx, list.get(leftchildidx));
list.set(leftchildidx, temp);
curidx = leftchildidx;
}
else
break;
}
else if(list.get(leftchildidx) <= list.get(rightchildidx))
{
if(list.get(curidx) < list.get(rightchildidx))
{
int temp = list.get(curidx);
list.set(curidx, list.get(rightchildidx));
list.set(rightchildidx, temp);
curidx = rightchildidx;
}
else
break;
}
}
}
return result;
}
@Override
public String toString() {
return list.toString();
}
}public class MyHeapTest {
public static void main(String[] args) {
MyHeap heap = new MyHeap();
heap.Insert(15);
heap.Insert(10);
heap.Insert(8);
heap.Insert(5);
heap.Insert(4);
heap.Insert(20);
System.out.println(heap);
System.out.println(heap.Pop());
System.out.println(heap);
}
}