1. 신장트리란
Spanning Tree, 또는 신장 트리라고 불리움
그래프가 있다고 하자
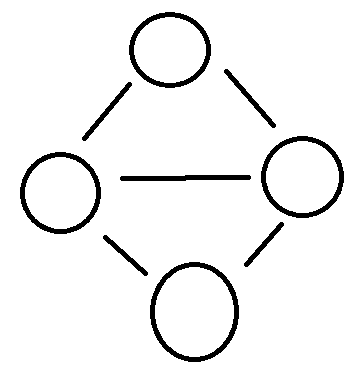
이 그래프의 연결을 끊어버려
그리고 트리가 되도록 연결한다(사이클이 없이 모든 노드 연결되야함)
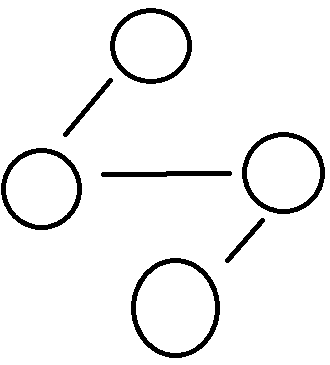
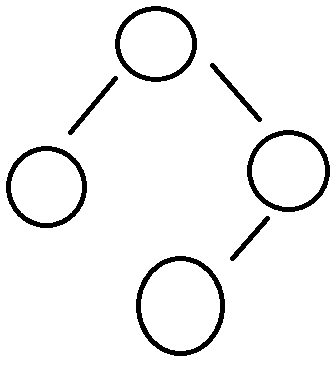
경우의 수가 더 있을것이다. 어쨋든 이것을 신장트리라고 한다
2. 최소 신장트리
Minimum Spanning Tree, MST 라고 불리움
다시 그래프를 보자 간선마다 가중치가 있다 이 값을 가장 작은것만 연결하면서 트리로 만들면 최소 신장 트리가 된다
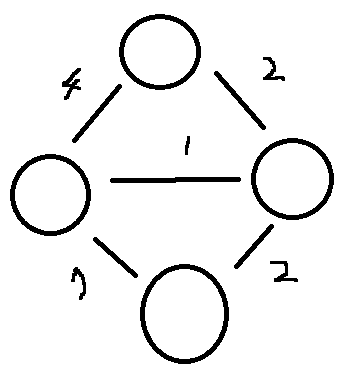
최소신장트리를 만들었다!
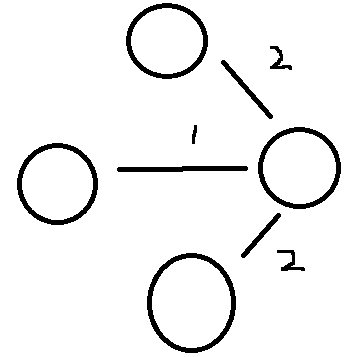
3.최소 신장 트리 알고리즘
그래프에서 최소 신장 트리를 찾을 수 있는 알고리즘이 존재함
대표적인 최소 신장 트리 알고리즘
Kruskal's algorithm
Prim's algorithm
4.크루스칼 알고리즘
1.모든 정점의 연결을 끊는다. 절단한다!!
2.모든 간선중에서 가장 가중치가 작은 간선 부터 점차 큰 것으로 연결한다. 다시말해 오름차순으로 찾아서 연결한다는것!. 이때 사이클이 만들어지는 간선은 패스하고 연결한다. 그러다 보면 모든 정점이 연결될것이다 그럼 끝!
3. 이때 사이클이 생기는지 안생기는지 판단여부는 Union-Find 알고리즘을 사용한다
5.Union-Find 알고리즘
union-find로 Disjoint Set을 만든다
Disjoint set 이란 중복 없는 부분집합 자료구조이다
크루스칼에 적용해본다면 연결된 엣지들의 집합과 새로 연결할 엣지의 집합이 서로 중복된 원소들이 있는지 확인할 수 있다는 말이다
어떻게 서로 중복이 되는지 알 수 있을까?
크루스칼 알고리즘에서 최소 가중치 엣지부터 연결한다고 하였다 이때 연결된 노드들은 트리구조로 관리한다.
R 은 루트노드라고 하자 1번과 2번을 연결하려고 한다
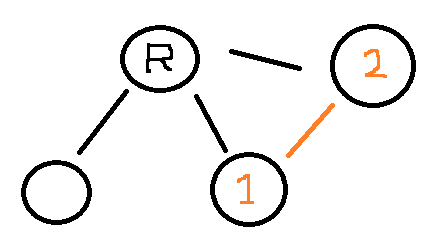
하지만 이것은 초록색의 집합에 오렌지색의 집합이 추가 되는것과 같다. 중복이 된다는것이다. 이것을 막아야 사이클이 만들어지지 않는다. 이것을 막는 방법은 1번과 2번의 루트노드를 찾아서 비교해보면 된다. 같은 루트노드라면 1번과 2번이 연결될때 사이클이 생기고 이것은 트리구조가 아니게 된다는 의미 이다.
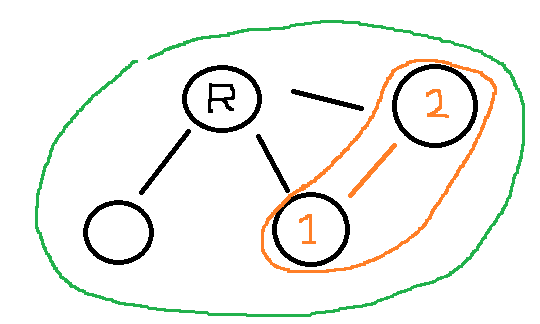
Union-Find 알고리즘의 고려할 점
이제 사이클을 피하며 연결할 수 있게 되었다 근데 또 문제가 있다. 연결할때 최악의 경우 한줄로 길게 늘어선 마치 링크드 리스트와 같은 트리가 될 수도 있다. 시간복잡도가 O(n)이 된다. 이를 해결하기위해 union-by-rank, path compression 기법을 사용한다고 한다
union-by-rank
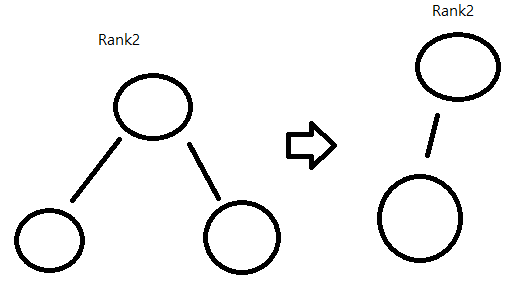
루트노드의 랭크(높이, 또는 레벨) 가 낮은것을 높은것에 연결
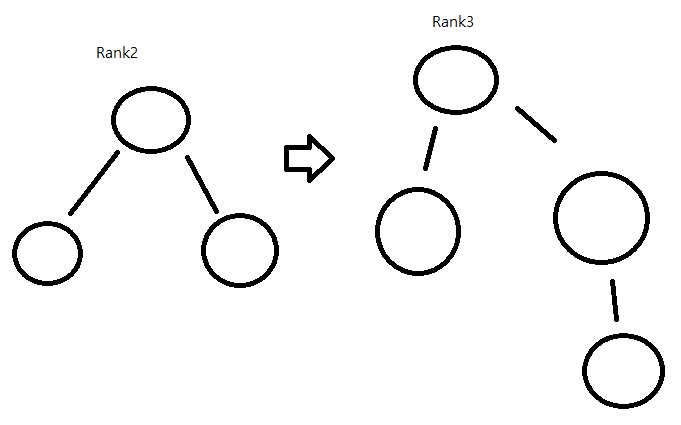
만약 동일한 경우 한쪽의 랭크를 높여서 붙인다
이러게 되면 트리의 복잡도가 O(logn)이 된다
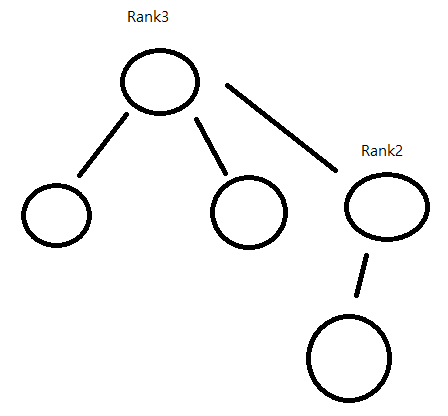
path compression
노드 탐색시 노드들을 루트노드에 연결시켜 버림!
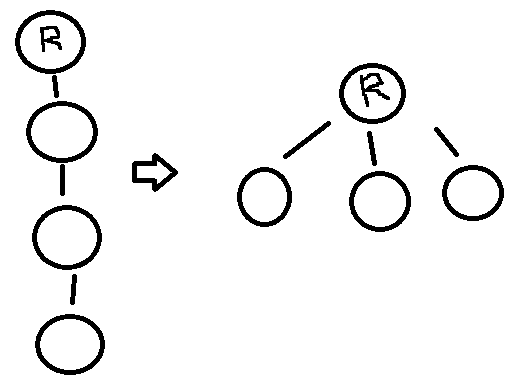
union-by-rank, path compression 를 같이 사용면 상수에 가까운 시간복잡도를 갖는다 O(1)에 가깝다고 한다..
구현하는걸 보고 나름 이해했다고 생각하고 구현했는데 1시간이나 걸렸다...
출력결과: [fV:A, sV:D, weight:5], [fV:C, sV:E, weight:5], [fV:D, sV:F, weight:6], [fV:A, sV:B, weight:7], [fV:B, sV:E, weight:7], [fV:E, sV:G, weight:9]
public class Edge implements Comparable {
public int weight;
public String firstV;
public String secondV;
public Edge() {
}
public Edge(int weight, String firstV, String secondV) {
this.weight = weight;
this.firstV = firstV;
this.secondV = secondV;
}
@Override
public int compareTo(@NotNull Object o) {
return this.weight - ((Edge)(o)).weight;
}
@Override
public String toString() {
return "[fV:" + firstV + ", sV:" + secondV + ", weight:" + weight +"]";
}
}public class MyMST {
private HashMap<String, String> parent;
private HashMap<String, Integer> rank;
MyMST()
{
parent = new HashMap<>();
rank = new HashMap<>();
}
String find(String vertex)
{
if(parent.get(vertex) == vertex)
return vertex;
if(parent.get(vertex) == null)
return vertex;
String root = find(parent.get(vertex));
parent.put(vertex, root);
return root;
}
ArrayList<Edge> kruskal(ArrayList<String> vertices, ArrayList<Edge> edges)
{
ArrayList<Edge> mst = new ArrayList<>();
for(int i = 0; i < vertices.size(); ++i)
{
parent.put(vertices.get(i), vertices.get(i));
rank.put(vertices.get(i), 0);
}
Collections.sort(edges);
for(int i = 0; i < edges.size(); ++i)
{
Edge curEdge = edges.get(i);
String root1 = find(curEdge.firstV);
String root2 = find(curEdge.secondV);
if(root1.equals(root2) == false)
{
mst.add(curEdge);
if(rank.get(root1) > rank.get(root2))
{
parent.put(root2, root1);
}
else
{
parent.put(root1, root2);
if(rank.get(root1) == rank.get(root2))
{
rank.put(root2, rank.get(root2)+1);
}
}
}
}
return mst;
}
}public class MyMSTTest {
public static void main(String[] args) {
ArrayList<String> vertices = new ArrayList<String>(Arrays.asList("A", "B", "C", "D", "E", "F", "G"));
ArrayList<Edge> edges = new ArrayList<Edge>();
edges.add(new Edge(7, "A", "B"));
edges.add(new Edge(5, "A", "D"));
edges.add(new Edge(7, "B", "A"));
edges.add(new Edge(8, "B", "C"));
edges.add(new Edge(9, "B", "D"));
edges.add(new Edge(7, "B", "E"));
edges.add(new Edge(8, "C", "B"));
edges.add(new Edge(5, "C", "E"));
edges.add(new Edge(5, "D", "A"));
edges.add(new Edge(9, "D", "B"));
edges.add(new Edge(7, "D", "E"));
edges.add(new Edge(6, "D", "F"));
edges.add(new Edge(7, "E", "B"));
edges.add(new Edge(5, "E", "C"));
edges.add(new Edge(7, "E", "D"));
edges.add(new Edge(8, "E", "F"));
edges.add(new Edge(9, "E", "G"));
edges.add(new Edge(6, "F", "D"));
edges.add(new Edge(8, "F", "E"));
edges.add(new Edge(11, "F", "G"));
edges.add(new Edge(9, "G", "E"));
edges.add(new Edge(11, "G", "F"));
MyMST mst = new MyMST();
ArrayList<Edge> result = mst.kruskal(vertices, edges);
System.out.println(result);
}
}