⚡ Array 3
📌 완전 검색(Exhaustive Search)
🔷 문제의 해법으로 생각할 수 있는 모든 경우의 수를 나열해보고 확인하는 기법
Brute-force(브루트포스)혹은Generate-and-Test기법이라고도 한다.- 모든 경우의 수를 테스트한 후, 최종 해법을 도출한다.
- 일반적으로 경우의 수가 상대적으로 작을 때 유용하다.
- 모든 경우의 수를 생성하고 테스트하기 때문에 수행 속도는 느리지만, 해답을 찾아내지 못할 확률이 작다.
💡 알고리즘 문제 풀이 시에 완전 검색으로 먼저 접근한 뒤에 다른 알고리즘으로 성능 개선을 하는 것이 가장 바람직하다.
🔷 순열(Permutation): 서로 다른 것들 중 몇 개를 뽑아서 한 줄로 나열하는 것
- 서로 다른 n개 중 r개를 택하는 순열: nPr = n (n-1) (n-2) ... 2 * 1
- npn = n! (Factorial)
int [] cards = {1 ,5, 9};
int N = cards.length;
// 반복문을 이용한 순열 만들기
// 첫번째 카드 뽑기
for(int i =0; i < N; i++) {
// 두번째 카드 뽑기
for(int j =0; j < N; j++) {
// i와 j가 같지 않을 떄
if(i != j) {
for(int k =0; k < N; k++) {
// k가 i, j 와 같지 않을 때
if(k != i && k != j) {
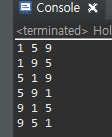
System.out.println(cards[i] + " " + cards[j] + " " + cards[k]);
}
}
}
}
}
📌 탐욕(Greedy) 알고리즘
🔷 최적해를 구하는 데 사용되는 가장 근시안적인 방법
- 여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도달한다.
- 각 선택의 시점에서 이루어지는 결정은 지역적으로는 최적이지만 그 선택들을 계속 수집하여 최종적인 해답을 만들었다고 하여, 그것이 최적이라는 보장은 없다.
머릿속에 떠오르는 생각을 검증없이 바로 구현하면 그게 곧 그리디
(난가?)
🔷 동작 과정
1) 해 선택: 현재 상태에서 부분 문제의 최적 해를 구한 뒤, 이를 부분 해 집합에 추가한다.
2) 실행 가능성 검사: 새로운 부분해 집합이 실행 가능한지를 확인한다. 곧, 문제의 제약 조건을 위반하지 않는지 검사한다.
3) 해 검사: 새로운 부분해 집합이 문제의 해가 되는지를 확인하고 아직 전체 문제의 해가 완성되지 않았다면 1)의 해 선택부터 다시 시작한다.
📌 2차원 배열
🔷 선언
- 2차원 이상의 다차원 배열은 차원에 따라 index를 선언
- 2차원 배열의 선언: 세로길이(행의 개수), 가로길이(열의 개수)를 필요로 한다.
int [][] arr = new int [2][3];🔷 순회
- n x m 배열의 n * m 개의 모든 원소를 빠짐 없이 조사하는 방법
int [][] arr = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
int N = arr.length;
int M = arr[0].length;
// 행 우선 순회
System.out.print("행 우선 순회: ");
for(int i = 0; i < N; i++) {
for(int j = 0; j < M; j++) {
System.out.print(arr[i][j] + " ");
}
}
System.out.println();
// 행 우선 역순회
System.out.print("행 우선 역순회: ");
for(int i = 0; i < N; i++) {
for(int j = 0; j < M; j++) {
System.out.print(arr[i][M-1-j] + " ");
}
}
System.out.println();
// 열 우선 순회
System.out.print("열 우선 순회: ");
for(int j = 0; j < M; j++) {
for(int i = 0; i < N; i++) {
System.out.print(arr[i][j] + " ");
}
}
System.out.println();
// 열 우선 역순회
System.out.print("열 우선 역순회: ");
for(int j = 0; j < M; j++) {
for(int i = 0; i < N; i++) {
System.out.print(arr[N-1-i][j] + " ");
}
}
System.out.println();
// 지그재그 순회
System.out.print("지그재그 순회: ");
for(int i = 0; i < N; i++) {
for(int j = 0; j < M; j++) {
System.out.print(arr[i][j + (M-1-j-j) * (i%2)] + " ");
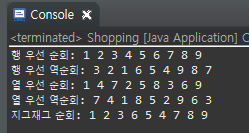
}
}

감사합니다. 이런 정보를 나눠주셔서 좋아요.