⚡ Array 2
📌 검색 (Search)
🔷 저장되어 있는 자료 중에서 원하는 항목을 찾는 작업
- 목적하는 탐색 키를 가진 항목을 찾는 것
탐색 키(search key): 자료를 구별하여 인식할 수 있는 키- 검색의 종류
순차 검색(sequential search)이진 검색(binary search)인덱싱(indexing)
⭐ 순차 검색
🔷 일렬로 되어 있는 자료를 순서대로 검색하는 방법
- 가장 간단하고 직관적인 검색 방법
- 배열이나 연결 리스트 등 순차구조로 구현된 자료구조에서 원하는 항목을 찾을 때 유용함
- 알고리즘이 단순하여 구현이 쉽지만, 검색 대상의 수가 많은 경우에는 수행 시간이 급격히 증가
🔷 정렬되어 있지 않은 경우
- 검색 과정
1) 첫 번째 원소부터 순서대로 검색 대상과 키 값이 같은 원소가 있는지 비교하며 찾는다.
2) 키 값이 동일한 원소를 찾으면 그 원소의 인덱스를 반환한다.
3) 자료구조의 마지막에 이를 때까지 검색 대상을 찾지 못하면 검색 실패 - 찾고자 하는 원소의 순서에 따라 비교 회수가 결정됨 (
O(n))
public static boolean searchForNoSort(int key) {
for(int i = 0; i < arr.length; i++) {
if(arr[i]==key)
return true;
}
return false;
}🔷 정렬되어 있는 경우
- 검색 과정
1) 자료가 오름차순으로 정렬된 상태일 때
2) 자료를 순차적으로 검색하면서 키 값을 비교하여, 원소의 키 값이 검색 대상의 키 값보다 크면 찾는 원소가 없다는 것이므로 검색을 종료한다. - 정렬이 되어있으므로, 검색 실패를 반환하는 경우 평균 비교 회수가 반으로 줄어든다.
시간복잡도는 O(n)으로 같다.
⭐ 이진 검색
🔷 자료의 가운데에 있는 항목의 키 값과 비교하여 다음 검색의 위치를 결정하고 검색을 계속 진행하는 방법
- 목적 키를 찾을 때까지 이진 검색을 순환적으로 반복 수행함으로써 검색 범위를 반으로 줄여가면서 보다 빠르게 검색을 수행함
❗ 이진 검색을 하기 위해서는 자료가 정렬된 상태여야 한다.
- 검색 과정
1) 자료의 중앙에 있는 원소를 고른다.
2) 중앙 원소의 값과 찾고자 하는 목표 값을 비교한다.
3) 목표 값이 중앙 원소의 값보다 작으면 자료의 왼쪽 반에 대해서 새로 검색을 수행하고, 크다면 자료의 오른쪽 반에 대해서 새로 검색을 수행한다.
4) 찾고자 하는 값을 찾을 때까지 1~3의 과정을 반복한다.
public static boolean binarySearch(int key) {
int st = 0;
int ed = arr2.length-1;
while(st <= ed) {
int mid = (st+ed) / 2;
if(arr2[mid] == key)
return true;
else if(arr2[mid] > key) {
ed = mid-1;
}
else {
st = mid+1;
}
}
return false;
}🌟 Arrays.binarySearch()로 구현이 이미 되어있다.
📌 선택 정렬(Selection sort)
🔷 셀렉션 알고리즘
- 저장되어 있는 자료로부터 k번째로 큰 혹은 작은 원소를 찾는 방법
- 최소값, 최대값 혹은 중간 값을 찾는 알고리즘을 의미하기도 한다.
🔷 선택 과정
- 정렬 알고리즘을 이용하여 자료를 정렬하기
- 원하는 순서에 있는 원소 가져오기
🔷 선택 정렬
- 주어진 자료들 중 가장 작은 값의 원소부터 차례대로 선택하여 위치를 교환하는 방식
💡 셀렉션 알고리즘을 전체 자료에 적용한 것
- 정렬 과정
1) 주어진 리스트 중에서 최소 값을 찾는다.
2) 그 값을 리스트의 맨 앞에 위치한 값과 교환한다.
3) 맨 처음 위치를 제외한 나머지 리스트를 대상으로 위의 과정을 반복한다.💡 O(n^2)
public static void selectionSort() { int N = arr3.length; // 한 사이클이 종료될 때마다 하나씩 정렬되므로 N-1번 // i번째의 자리를 정렬 for(int i = 0; i < N-1; i++) { int minIdx = i; //i번째가 가장 작다고 초기화 for(int j = i+1; j<N; j++) { if(arr3[j] < arr3[minIdx]) { minIdx = j; } } int tmp = arr3[i]; arr3[i] = arr3[minIdx]; arr3[minIdx] = tmp; } System.out.println(Arrays.toString(arr3)); }
📌 카운팅 정렬
🔷 항목들의 순서를 결정하기 위해 집합에 각 항목이 몇 개씩 있는지 세는 작업을 하여, 선형 시간에 정렬하는 효율적인 알고리즘
❗ 제한 사항
- 정수나 정수로 표현할 수 있는 자료에 대해서만 적용 가능
- 각 항목의 발생 회수를 기록하기 위해, 정수 항목으로 인덱스 되는 카운트들의 배열을 사용하기 때문
- 카운트들을 위한 충분한 공간을 할당하려면 집합 내의 가장 큰 정수를 알아야 한다.
💡 O(n + k): n은 배열의 길이, k는 정수의 최대값
🔷 정렬 과정
1) Data에서 각 항목들의 발생 횟수를 세고, 정수 항목들로 직접 인덱스 되는 카운트 배열 counts에 저장한다.
2) 정렬된 집합에서 각 항목의 앞에 위치할 항목의 개수를 반영하기 위해 counts의 원소를 조정한다. (누적합)
3) 정렬한 자료를 넣을 배열을 만들고 Data의 뒤에서 부터 확인한다. 확인한 값과 일치하는 count의 인덱스에 들어있는 값을 1 빼고 그 값에 해당하는 새로 만든 배열의 인덱스에 확인한 값을 넣는다.
🤷♂️ 왜 뒤에서부터 확인을 하죠?
카운팅 정렬의 특징인안정 정렬을 위해서 뒤부터 확인함. 그래야 정렬이 보장됨.
💡
안정 정렬
같은 값을 가지는 복수의 원소들이 정렬 후에도 정렬 전과 같은 순서를 가지는 것
int nums[] = {8, 8, 12, 21 ,21 ,19, 3, 35, 60};
int N = nums.length;
// 1. 데이터 중 가장 큰 값을 알아야한다.
int K = -1;
for(int i = 0; i < N; i++) {
if(K < nums[i])
K = nums[i];
} // 가장 최대값을 찾는 for
int [] count = new int [K+1]; // 0~60: 61칸 짜리 count 배열 생성
// 2. 개수 카운팅
for(int i = 0; i < N; i++) {
// nums[i] 값을 인덱스로 하여 카운트를 증가
count[nums[i]]++;
}
// 3. 누적합 구하기 (들어갈 수 있는 위치를 결정하고 안정정렬을 가능하게 함)
for(int i = 1; i < count.length; i++) {
count[i] += count[i-1];
}
// 4. 새 배열을 만들고 원본 배열의 뒤에서부터 순회를 하며 정렬된 배열에 차곡차곡 저장한다.
int [] sortArr = new int[N];
for(int i = N-1; i >= 0; i--) {
// 지금 저장하고 싶은 값: nums[i]
// 저장 하고싶은 위치: count[nums[i]]-1 -> 하고나서 한번 더 count[nums[i]]--;
sortArr[--count[nums[i]]] = nums[i];
}
System.out.println(Arrays.toString(sortArr));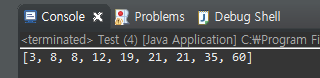
❗ 값 중 최대 값이 지나치게 크면 메모리 낭비가 발생할 수 있다. (배열이 상당히 길어짐)
그래서 값이 모여있고, 최대 값이 작은 경우에 사용을 추천