Lower Bound와 Upper Bound는 이분 탐색에서 파생된 알고리즘이다.
이분 탐색은 원하는 값의 위치를 찾는 과정이라면 이것과 조금 다르게
해당하는 값의 이상이 되는 첫번째 위치를 찾는 Lower Bound와
해당하는 값의 초과가 되는 첫번째 위치를 찾는 Upper Bound가 있다.
보통 결정알고리즘이라고 부르며
어떤 범위 안에 답이 있다라는 확신이 있는 경우
"가장 가까운 말의 최대 거리를 구하시오."
"레코드 안에 넣을 수 있는 최대 레코드 길이를 구하시오."처럼
저 답에 대한 범위를 확정할 수 있을 때 이분 탐색을 통해서 그 값에 가까워지는 것이다.
그렇다면 저 두가지 중 어느 것에 해당되느냐를 고민할 수 있다.
사실 이 두가지를 굳이 나눌 필요는 없지만
중간값이 정답에 포함되는지가 어느 쪽에서 결정되느냐에 따라 다르다.
-
기준이 되는 값보다 작은 값도 정답에 포함되는지
int lo = max; int hi = arr_sum; int answer=0; while(lo<=hi){ int mid = (lo+hi)/2; int T =1; int sum=0; for(int i=0 ;i<N;i++){ if(sum+arr[i]>mid){ sum=arr[i]; T++; // 마지막 한장이 작을 수도 있으므로 기본값 1부터 시작 }else sum+=arr[i]; } if(T<=M) { //레코드 개수보다 작은 작은 값도 정답에 포함됨 answer=mid; hi = mid-1; } else { lo = mid+1; } } -
기준이 되는 값보다 큰 값도 정답에 포함되는지
int lo = 1; int hi = arr[N-1]; int answer =0; while(lo<=hi){ int mid = (lo+hi)/2; int horse=1; int start=0; for(int i=1;i<N;i++){ if(arr[i]-arr[start]>=mid) { horse++; start=i; } } if(horse<C) hi = mid-1; else { //말의 수가 기준 값보다 많은 것도 정답에 포함된다. answer=mid; lo=mid+1; } }
이렇게 두가지 여부에 따라 결정하면 된다. 따라서 이 문제는
첫번째, 정답의 하한선과 상한선을 결정한다.
하지만 하한선과 상한선의 범위를 너무 줄이려고 하다보면 정답의 범위와 벗어날 수 있으니 여유롭게 잡도록
두번째, 무엇을 기준으로 나아갈 것인가? 보통은 그 주체를 준다. 말의 수라던지, 레코드의 수라던지 이걸 기준으로 해야한다.
세번째, 기준값과 비교된 값을 도출하는 함수를 만들어야 한다.
네번째, while문을 통해서 mid값을 조정하는데 while문제 들어가는 조건문이 lo<=hi인 경우에는 lo와 hi가 만날 수 있다는 전제하이기 때문에
lo=mid+1, hi=mid-1로 나아가야 한다.
- Lower Bound : 어떤 값이 주어졌을 때 그 값 이상이 되는 첫번째의 위치를 찾아간다.
◯ -> ● ●
start end
딱 두개의 값이 남았을 때 상황 end는 해당하는 값이 시작되는 처음 위치를 향하고 있다.
end는 해당하는 값의 자리에서 더이상 뒤로 가지 못하도록 target값이 존재하는 위치에 있다.
lo = 0;
hi = arr.length-1;
// lo와 hi의 값이 같아지면 나온다.
while(lo<hi){
int mid = (lo+hi)/2;
if(arr[mid]>=target) hi = mid;
else lo =mid+1;
}
- Lower Bound : 어떤 값이 주어졌을 때 그 값이 초과가 되는 첫번째의 위치를 찾아간다.
● ◯ <- ◯
start end
마지막 딱 두개의 값만 남았을 때 상황
mid가 target에 해당하는 경우 거기가 아닌 하나 더 나아가서 자리를 잡기 때문에 mid+1로 설정된다.
lo = 0;
hi = arr.length-1;
// lo와 hi의 값이 같아지면 나온다.
while(lo<hi){
int mid = (lo+hi)/2;
if(arr[mid]>target) hi = mid;
else lo =mid+1;
}
응용문제 백준 2805번
을 풀어보고자 한다.
문제는 나무가 있을 때 필요한 길이만큼 벌목하는 것인데
나무가 일렬로 있고 최소한의 훼손을 목적으로 한다.
따라서 기계의 높이를 어디까지 했을 때 원하는 길이만큼 훼손을 최소한 해서 가져갔을 수 있는지가 문제이다.
여기서 둘중에 무엇을 사용해야 할지 정한다.
또한 java 언어의 경우 변수형을 무엇으로 해야하는지 꼭 유심히 보자.
보면
"나무의 수 N과 상근이가 집으로 가져가려고 하는 나무의 길이 M이 주어진다."
(1 ≤ N ≤ 1,000,000, 1 ≤ M ≤ 2,000,000,000)
라고 되어져 있어서 총 길이를 더할 때의 변수가 int(최대 10자리 자연수)가 아닌 long(최대 19자리)을 이용한다.
왜냐하면 나의 길이가 2,000,000,000일 때 나무 수가 1,000,000이라면 sum은 2,000,000,000,000,000보다 작을 것이다. 따라서 꼭 변수형에 유의해서 풀어보자.
일단 이 문제에서 우리는 무조건! array를 사용하지 않고 이렇게 응용될 수 있다는 것을 알아야한다.
자 이제는 무엇을 정답으로 포함할 것인가 결정하자. 우리는 큰 값을 답에 포함해야 한다. (구하려는 길이가 6이고 나무 길이가 5과 8인 경우 4의 높이에서 잘린다면 나무막대기는 5가 생김-> 부족해서 더 내려간다고 해서 딱 6의 길이를 얻을 수 없음)
import java.util.*;
import java.io.*;
class Main{
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine()," ");
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int[] trees = new int[N];
int min=0;
int max=0;
st = new StringTokenizer(br.readLine()," ");
for(int i=0;i<N;i++){
trees[i] = Integer.parseInt(st.nextToken());
if(max<trees[i]){
max = trees[i];
}
}
// sum이 M을 초과하는 첫 숫자를 구하자!
// 처음으로 초과하는 경우를 구한 Upper Bound
while(min<max){
int mid = (min+max)/2;
long sum=0;
for(int treeHeight : trees){
if(treeHeight-mid>0) {
sum+=(treeHeight-mid);
}
}
if(sum<M) {
max = mid;
} else {
min =mid+1;
}
}
System.out.println(min-1);
}
}응용문제 인프런 알고리즘 강의에 있는 뮤직비디오 문제
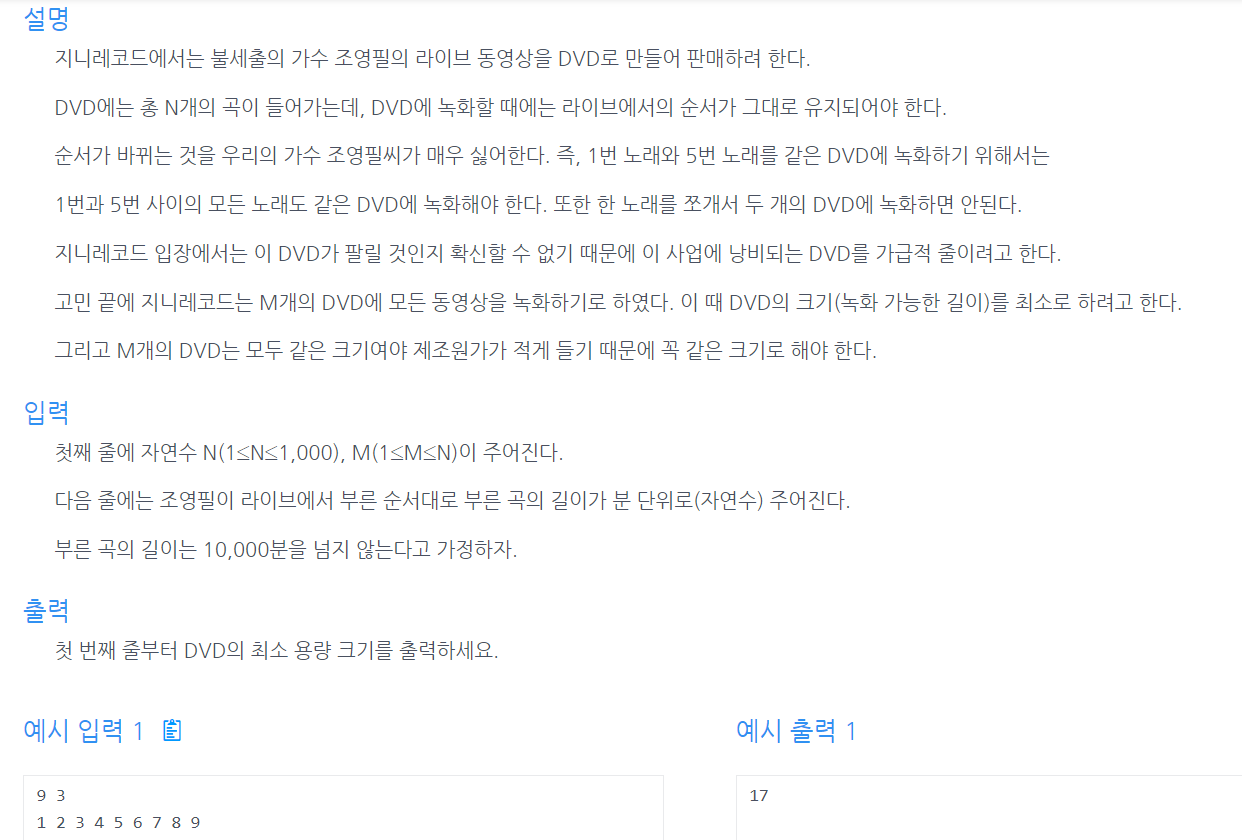
import java.util.*;
import java.io.*;
class Main{
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine()," ");
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int hi=0;
int lo = 1;
int[] record = new int[N];
st = new StringTokenizer(br.readLine()," ");
for(int i=0;i<N;i++){
record[i] = Integer.parseInt(st.nextToken());
hi+=record[i];
}
int answer=0;
while(lo<=hi){
int mid=(lo+hi)/2;
int sum=0;
int cd=0;
for(int i=0;i<N;i++){
sum+=record[i];
if(sum>mid){
cd++;
sum=record[i];
}else if(sum==mid){
cd++;
sum=0;
}
}
if(sum!=0) cd++;
if(cd<=M){
answer=mid;
hi=mid-1;
} else{
lo=mid+1;
}
}
bw.write(Integer.toString(answer));
bw.flush();
bw.close();
br.close();
}
}