백준에서 재귀함수를 이용해서 피보나치 수열을 푸는데 계속 메모리 초과가 나오는 것이다. 따라서 재귀함수보다 더 효율적인 방법으로 Dynamic Programming 기법에 대해서 알아보고자 한다.
Dynamic Programming 기법은 작은 문제를 풀고 그 결과를 저장한 후 큰 문제를 풀 때 이용하는 방식의 bottom-up방식과 큰 문제를 풀고 그 결과를 저장한 후 작은 문제를 풀 때 이용하는 top-down 방식이 있다. 봤을 때 더 직관적인 것은 bottom-up 방식이기 때문에 나는 bottom-up 방식을 이용해서 문제를 풀어보려고 한다.
코드를 통해서 살펴보자
재귀함수를 이용한 피보나치 수열
public static long fibonacci(int n){
if(n==1 || n==2) return 1;
return fibonacci(n-1) + fibonacci(n-2);
}bottom-up
class Main{
public static long[] dq;
public static void main(String[] args) {
int n =100;
dq[1]=1;
dq[2]=1;
int result =fibonacci(n);
}
public static long fibonacci(int n){
if(n==1 || n==2) return 1;
for(int i=3;i<n;i++){
dq[i] =dq[i-1]+dq[i-2];
}
return dq[n];
}
}top-down
class Main{
public static long[] dq;
public static void main(String[] args) {
int n =100;
dq[1]=1;
dq[2]=1;
int result =fibonacci(n);
}
public static long fibonacci(int n){
if(n==1 || n==2) return 1;
if(dq[n]!=0) return dq[n]
return dq[n] = fibonacci(n-1) + fibonacci(n-2);
}
}확실히 bottom-up 방식이 더 직관적이다.
응용문제 백준의 1003번
를 살펴보려고 한다.
그 이전에 저장한 0과 1의 개수를 그대로 저장한 채 넘겨주는 것이다.
import java.util.*;
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int T = Integer.parseInt(br.readLine());
zeroOne[] dp = new zeroOne[41];
dp[0] = new zeroOne(1,0);
dp[1] = new zeroOne(0,1);
for (int i = 0; i < T; i++) {
int input = Integer.parseInt(br.readLine());
zeroOne output =fibonacci(input,dp);
bw.write(Integer.toString(output.zero)+" "+Integer.toString(output.one)+"\n");
}
bw.flush();
bw.close();
br.close();
}
static class zeroOne {
private int zero;
private int one;
public zeroOne(int zero, int one){
this.zero = zero;
this.one = one;
}
}
public static zeroOne fibonacci(int N, zeroOne[] dp) {
if (N == 0) return dp[0];
if(N==1) return dp[1];
for(int i=2;i<=N;i++){
dp[i]= new zeroOne(dp[i-1].zero+dp[i-2].zero,
dp[i-1].one+dp[i-2].one);
}
return dp[N];
}
}
응용문제 백준의 11726번
을 풀어보았다.
처음에 이 문제가 dp로 풀어야하는지 접근이 어렵지만
그럴 때는 앞의 몇가지의 수를 대입해서 규칙을 발견해야 한다.
한가지 배워야할 부분은 오버플로우가 발생해서 중간중간마다 10007로 나누어줘야 한다는 것!
따라서 마지막에 10007로 나눈 나머지가 아니라
연산마다 해줘야 한다.
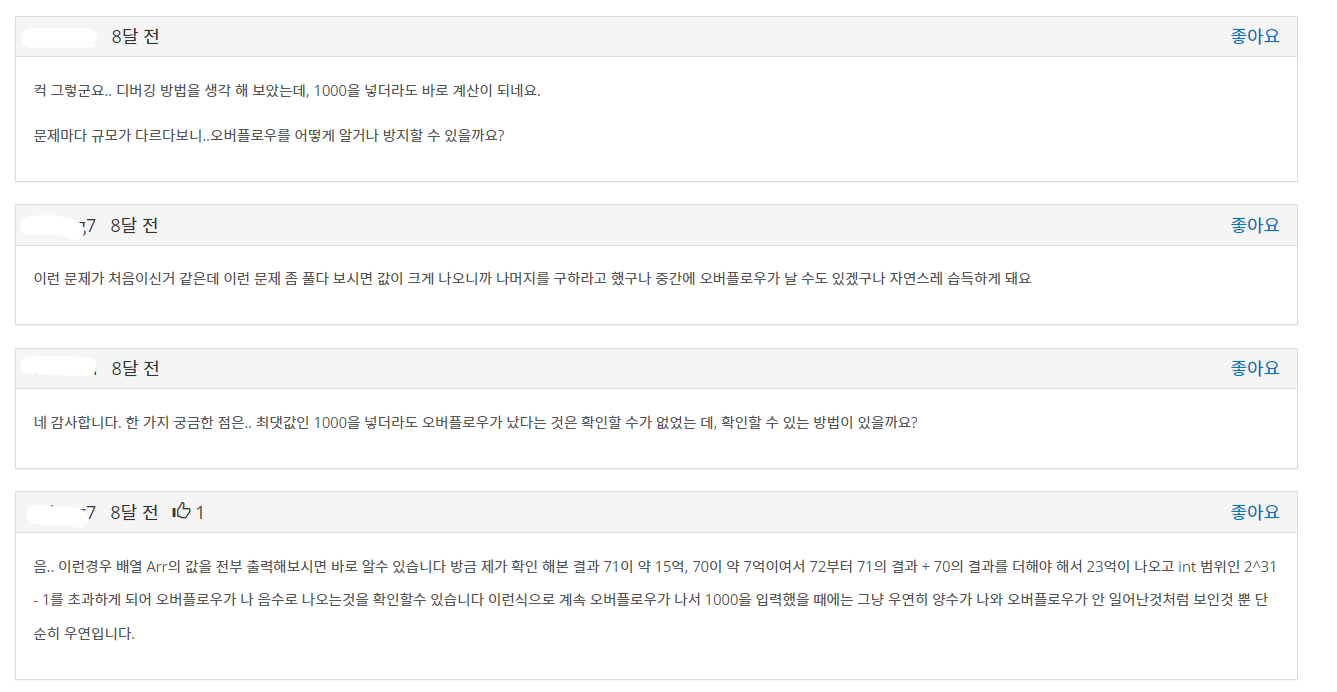
어쩜 이리 나랑 같은 생각을 하셨는지
같은 질문을 물어보셨고 어느 분이 친절하게 답변을 주셨다.
import java.util.*;
import java.io.*;
public class Main{
public static int[] dp = new int[1001];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
dp[1]=1;
dp[2]=2;
int N = Integer.parseInt(br.readLine());
int output= tile(N);
bw.write(Integer.toString(output));
bw.flush();
bw.close();
br.close();
}
public static int tile(int N ){
if(N==1) return 1;
if(N==2) return 2;
for(int i=3;i<=N;i++){
dp[i] =(dp[i-1]+dp[i-2])%10007;
}
return dp[N];
}
}응용문제 백준의 1463번
도 dp를 이용한다.
dp는 과거의 저장된 값을 이용하는 것이기 때문에
과거의 값을 어디로, 어떤 위치로 찾아갈 것인가
그리고 과거의 값을 활용할 수 있는가
이 두가지를 유심있게 봐야 한다.
일단 이 문제 3가지의 연산을 최소한의 방법으로 이용해서 마지막에 1을 남기는 것이다.
3가지 연산은
1을 뺀다.
2로 나눌 수 있는 경우 2로 나눈다.
3으로 나눌 수 있는 경우 3으로 나눈다.
처음에 3으로 먼저 나눌 수 있으면 나누고 안되면 2로 그다음 마지막에 1을 빼는 방법을 생각했지만 이는 잘못된 방법이다.
따라서 dynamic programming을 이용하는데 그 방법은 아래와 같다.
N의 값을 구한다고 가정하자.
첫번째, N-1에 저장된 값을 찾아간다. N은 dp[N-1]의 값에 -1이라는 연산을 한 것이다. 따라서 dq[N-1]+1 = dq[N]이 된다.
두번째, N/2가 저장된 값을 찾아간다. dp[N/2]는 N의 1/2된 값이다. 따라서 여기에 마지막에 2로 나눈 연산을 더한 한번 더한 값이 dp[N/2]+1 = dp[N]가 된다.
세번째, N/3가 저장된 값을 찾아간다. dp[N/3]는 N의 1/3된 값이다. 따라서 여기에 마지막에 3으로 나눈 연산을 더한 한번 더한 값이 dp[N/3]+1 = dp[N]가 된다.
이 세가지의 방법의 값을 모두 비교해서 가장 작은 값이 최소의 연산횟수가 된다.
import java.util.*;
import java.io.*;
public class Main{
public static int[] dq;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int n = Integer.parseInt(br.readLine());
dq = new int[n+2];
dq[0]=0;
dq[1]=0;
for(int i=2;i<=n;i++){
//1이 적은 곳에 가서 1 연산한거 더해주기
dq[i]=dq[i-1]+1;
//1/2 적은 곳 가서 거기에 2로 나눈 연산을 했으니 그 값에 +1
if(i%2==0) dq[i]= Math.min(dq[i],dq[i/2]+1);
//1/3 적은 곳 가서 거기에 3으로 나눈 연산을 했으니 그 값에 +1
if(i%3==0) dq[i]= Math.min(dq[i],dq[i/3]+1);
}
bw.write(Integer.toString(dq[n]));
bw.flush();
bw.close();
br.close();
}
}응용문제 백준의 2579번
을 풀어보고자 한다.
일단 dp는 과거의 자료를 저장해서 활용할 수 있는지에 대한 규칙을 발견하는게 중요한거 같다.
이 문제를 처음에 무엇으로 접근해야 하는지 감이 잡히지 않았는데
규칙을 발견하여 dynamic programming기법인지 알게 되었다.
계단 하나일 때 (arr[1]
계단 두개일 때 Math.max(arr[1]+arr[2],arr[2]);
계단 새개일 때 Math.max(arr[1]+arr[3],arr[2]+arr[3]);
계단 네개일 때
Math.max
( arr[1]+arr[2]+arr[4],arr[2]+arr[4], arr[1]+arr[3]+arr[4]);
네 개일 때 발견되었다.
dp[i] = Math.max(dq[i-2],dq[i-3]+arr[i-1])+arr[i];
import java.util.*;
import java.io.*;
public class Main{
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(br.readLine());
int[] dp = new int[N+1];
int[] arr = new int[N+1];
for(int i=1;i<=N;i++){
arr[i] = Integer.parseInt(br.readLine());
}
dp[1] =arr[1];
if(N>1) dp[2] = Math.max(arr[1]+arr[2],arr[1]);
for(int i=3;i<=N;i++){
dp[i] = Math.max(dp[i-2],dp[i-3]+arr[i-1])+arr[i];
}
bw.write(Integer.toString(dp[N]));
bw.flush();
bw.close();
br.close();
}
}응용문제 백준의 11053번
을 풀어보자.
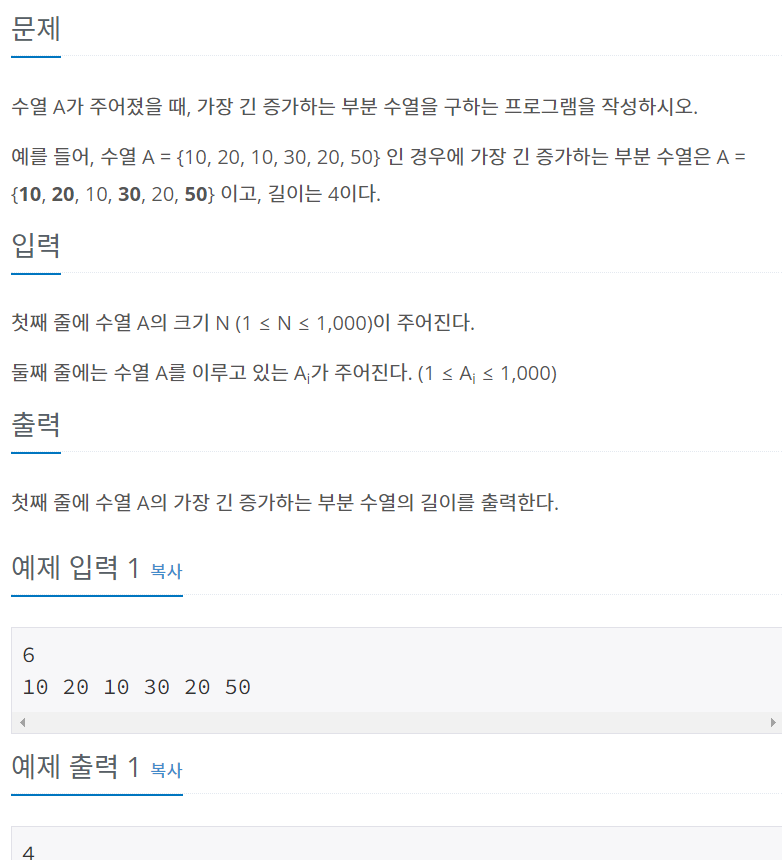
이 문제는 LIS(Longest Increasing Subsequence) 문제이다.
원소가 n개인 배열의 일부 원소를 골라내서 만든 부분 수열 중, 각 원소가 이전 원소보다 크다는 조건을 만족하고, 그 길이가 최대인 부분 수열
이 수열을 푸는 방법은 DP와 이분탐색이 있으며 나는
DP를 통해서 이 문제를 풀어보고자 한다.
