깊이우선탐색에 대해서 알아보자
깊이우선탐색은 모든 경로를 탐색한다.
어떤 수가 들어갈 경우 들어가지 않을 경우
숫자가 매겨진 노드의 모든 경로 탐색
모든 부분집합 등
모든 경로를 완전히 탐색한다고 보면 된다.
- 재귀함수가 이용된다.
- 상태를 저장할 수 있는 행렬이 필요한다.
- 그래프가 문제에 주어진다면 이를 저장할 인접행렬(범위가 넚다면 인접리스트)이 필요하다.
- 다시 거슬러 올라가기 때문에 상태를 원래 상태로 되돌릴 수 있는 부분이 필요하다(상태가 저장된 행렬을 원래 상태로 되돌리는 작업)
즉 DFS는 stack에 쌓아지는 걸 하나씩 해결해 나가는 것이다.
그렇게 해서 모든 경로를 다 탐색해보는 것이다.
안에서 안으로 계속 파고 들어서 모든 깊이를 다 탐색해 보는 것!
응용문제 합이같은 부분집합 구하기
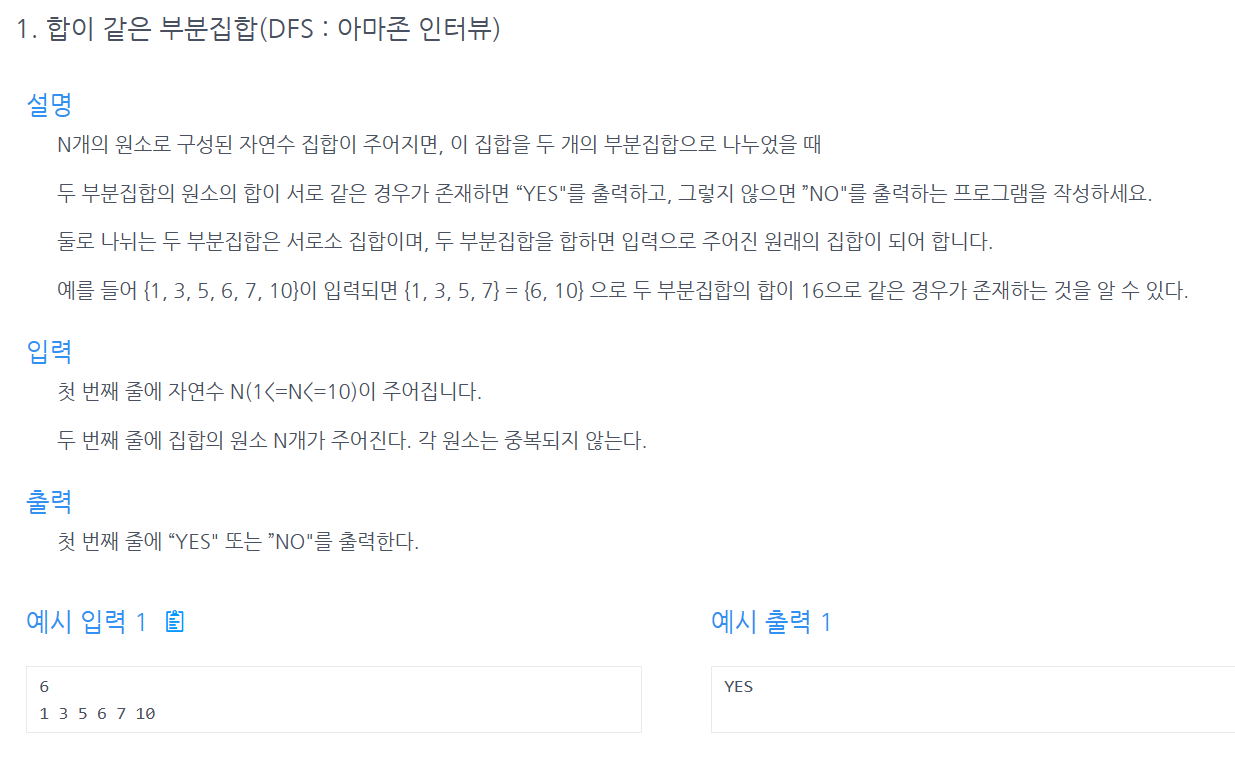
단순한 문제이다.
모든 부분집합을 구하되 거기서
부분집합으로 뽑힌 애들을 다 더하고
부분집합으로 뽑히지 않은 애들을 다 더해서
그 둘의 합이 같으면 출력이다.
YES가 등장하면 boolean tag를 false에서 true로 바꿔주는 부분을 추가했다.
import java.util.*;
import java.io.*;
public class Main{
static int[] arr;
static int[] ch;
static boolean tag =false;
static void DFS(int L,int N){
if(L==N+1){
int sum_1=0;
int sum_0=0;
for(int i=1;i<=N;i++){
if(ch[i]==1){
sum_1+=arr[i];
} else sum_0+=arr[i];
}
// System.out.println("sum_1: "+sum_1+", sum_0: "+sum_0);
if(sum_1==sum_0)
tag=true;
return;
}
else{
ch[L]=1;
DFS(L+1,N);
ch[L]=0;
DFS(L+1,N);
}
}
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(br.readLine());
arr= new int[N+1];
ch = new int[N+1];
StringTokenizer st = new StringTokenizer(br.readLine()," ");
for(int i=1;i<=N;i++){
arr[i] = Integer.parseInt(st.nextToken());
}
DFS(1,N);
if(tag==true)
bw.write("YES");
else bw.write("NO");
bw.flush();
bw.close();
br.close();
}
}응용문제 최대점수 구하기
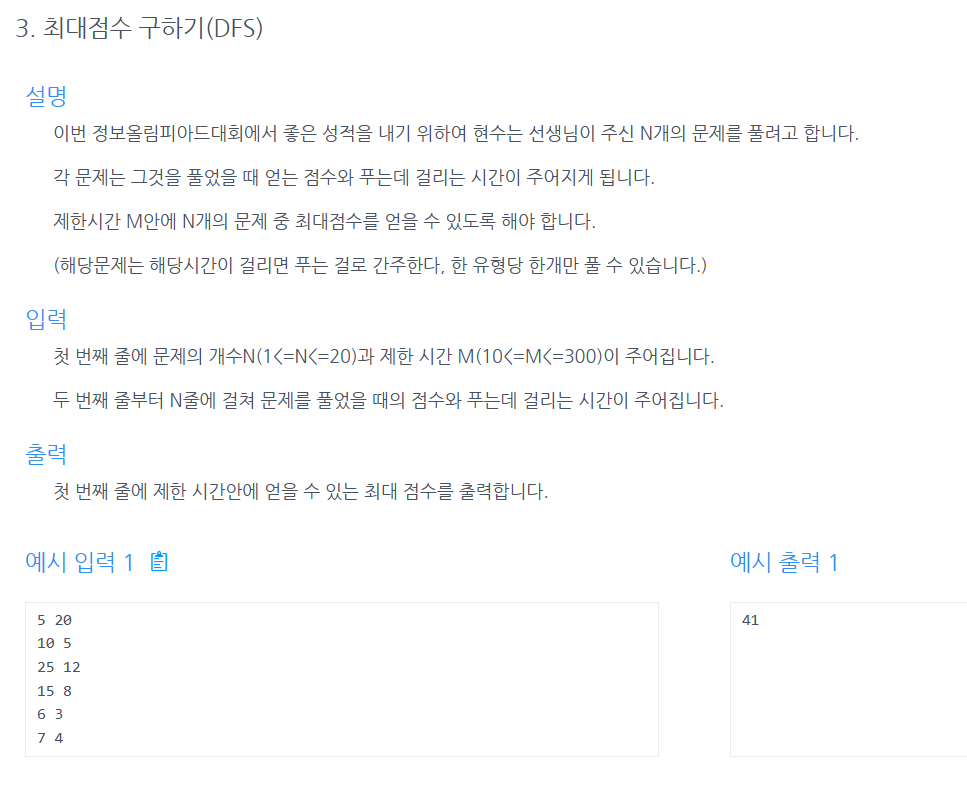
두 개의 배열을 생성해서 시간과 점수를 저장한다.
저 문제를 선택한 경우와 안 선택한 경우를 모두
조합해서 마찬가지로 모든 부분집합을 만들고
그 부분집합에 해당하는 원소들의 점수와 시간을 다 더해줍니다.
다 더한 시간이 주어진 제한시간보다 작거나 같은지 확인 &&
max값보다 큰지 확인
둘다 만족하면 max값을 해당 부분집합의 점수합으로 갱신하여 저장합니다.
import java.io.*;
import java.util.*;
public class Main{
static int N=0;
static int M =0;
static int[] ch;
static int[] score;
static int[] time;
static int max = Integer.MIN_VALUE;
static void DFS(int L){
if(L==N+1){
int sum_t=0;
int sum_s=0;
for(int i=1;i<=N;i++){
if(ch[i]==1){
sum_t+=time[i];
sum_s+=score[i];
}
}
if(sum_t<=M && max < sum_s) max = sum_s;
return;
}else{
ch[L]=1;
DFS(L+1);
ch[L]=0;
DFS(L+1);
}
}
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine()," ");
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
score= new int[N+1];
time= new int[N+1];
ch= new int[N+1];
for(int i=1;i<=N;i++){
st = new StringTokenizer(br.readLine()," ");
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
score[i]=a;
time[i]=b;
}
DFS(1);
bw.write(Integer.toString(max));
bw.flush();
bw.close();
br.close();
}
}응용문제 백준의 1012번
을 풀어보려고 한다.
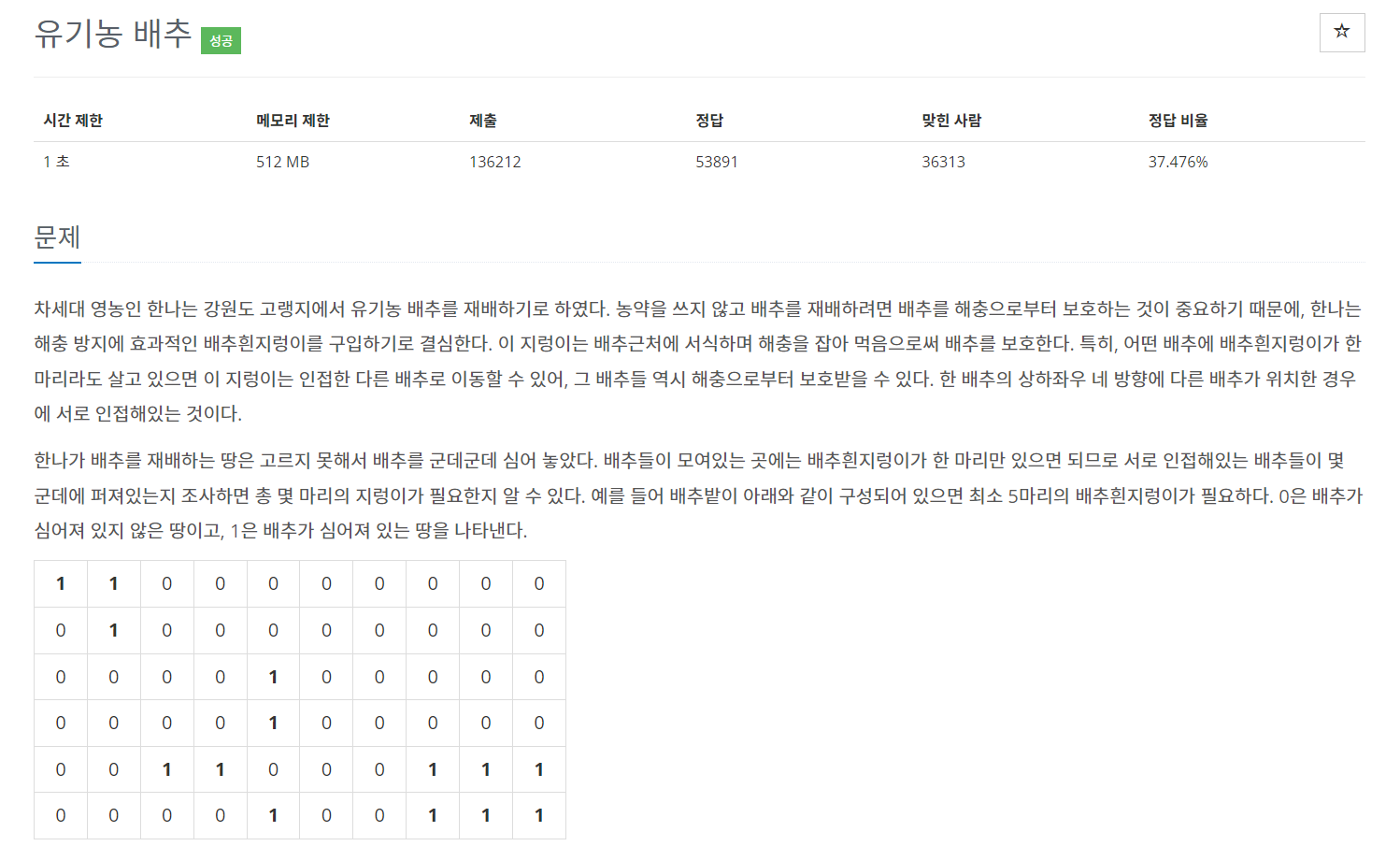
이 문제는 BFS로도 풀이가 가능하다.
일단 문제를 이해해보자
상하좌우로 배추벌레가 이동할 수 있는데 인접한 배추까지 다 가능하다.
즉, 인접해있으면 어디든 배추벌레가 이동할 수 있다는 것
따라서 배추벌레가 한번 들어가면 어디까지 이동할 수 있는지 표시해줘야 한다.
이동할 때 상하좌우로만 이동할 수 있으니 상으로 갈 때 DFS 호출(여기서 호출된 DFS가 또 상하좌우로 호출), 하로 갈때 DFS 호출..
이렇게 이동하다가 더 이상 먹을 배추가 없으면 뒤돌아 온다. 즉 stack에서 하나씩 제거되는 것이다.
이렇게 한번 들어가면 갈 수 있는 곳까지 이동하고 나온다.
import java.util.*;
import java.io.*;
public class Main{
static int N=0;
static int M=0;
static int[][] ch;
static int[][] arr;
static int[] cx = {0,1,0,-1};
static int[] cy = {-1,0,1,0};
static void DFS(int x, int y){
ch[x][y]=1;
for(int i=0;i<4;i++){
int x_bug = x+ cx[i];
int y_bug = y +cy[i];
if(x_bug>=0 && x_bug<N && y_bug>=0&&y_bug<M) {
if (arr[x_bug][y_bug] == 1 && ch[x_bug][y_bug] == 0) {
DFS(x_bug, y_bug);
}
}
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw =new BufferedWriter(new OutputStreamWriter(System.out));
int T = Integer.parseInt(br.readLine());
for(int i=0;i<T;i++){
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
int bug = Integer.parseInt(st.nextToken());
arr = new int[N][M];
ch = new int[N][M];
for(int j=0;j<bug;j++){
st= new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
arr[a][b]=1;
}
int cnt =0;
for(int z=0;z<N;z++){
for(int j=0;j<M;j++){
if(ch[z][j]==0 && arr[z][j]==1) {
DFS(z, j);
cnt++;
}
}
}
bw.write(Integer.toString(cnt)+"\n");
}
bw.flush();
bw.close();
br.close();
}
}+) 추가로 BFS로 푼 방법에 대해서도 풀이해보았다.
BFS로도 모든 경로를 탐색할 수 있다. 다만 DFS와 다르게 같은 레벨로 차근차근 접근할 수 있는 방법을 포함되게 할 수 있다.
import java.util.*;
import java.io.*;
public class Main{
static int N=0;
static int M=0;
static int[][] ch;
static int[][] arr;
static int[] cx = {0,1,0,-1};
static int[] cy = {-1,0,1,0};
static void BFS(int x, int y){
Queue<int[]> Q = new LinkedList<>();
int[] input = new int[2];
ch[x][y]=1;
input[0]=x;
input[1]=y;
Q.offer(input);
while(!Q.isEmpty()){
int[] output = Q.poll();
for(int i=0;i<4;i++){
int x_bug= output[0]+cx[i];
int y_bug = output[1]+cy[i];
if(x_bug>=0&&x_bug<N &&y_bug>=0 &&y_bug<M){
if(ch[x_bug][y_bug]==0 && arr[x_bug][y_bug]==1){
int[] bug = {x_bug,y_bug};
Q.offer(bug);
ch[x_bug][y_bug]=1;
}
}
}
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw =new BufferedWriter(new OutputStreamWriter(System.out));
int T = Integer.parseInt(br.readLine());
for(int i=0;i<T;i++){
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
int bug = Integer.parseInt(st.nextToken());
arr = new int[N][M];
ch = new int[N][M];
for(int j=0;j<bug;j++){
st= new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
arr[a][b]=1;
}
int cnt =0;
for(int z=0;z<N;z++){
for(int j=0;j<M;j++){
if(ch[z][j]==0 && arr[z][j]==1) {
BFS(z, j);
cnt++;
}
}
}
bw.write(Integer.toString(cnt)+"\n");
}
bw.flush();
bw.close();
br.close();
}
}응용문제 백준의 1260번
을 풀어보고자 한다.
이 문제는 DFS와 BFS를 둘다 구현해야 한다.
DFS : 하나를 잡으면 끝까지 간다.
BFS : 연결된 모든 경로를 차근차근 같은 단계로 간다.
import java.util.*;
import java.io.*;
public class Main{
static int N;
static int M;
static int V;
static int[][] graph;
static int[] ch_D;
static int[] ch_B;
static StringBuilder sb_D = new StringBuilder();
static StringBuilder sb_B = new StringBuilder();
static void DFS(int L){
boolean tag = false;
for(int i=1;i<=N;i++) {
if (graph[L][i] == 1 && ch_D[i] == 0) {
tag = true;
}
}
if(tag==false) return;
else{
for(int i=1;i<=N;i++){
if(graph[L][i]==1 &&ch_D[i]==0){
ch_D[i]=1;
sb_D.append(i).append(" ");
DFS(i);
}
}
}
}
static void BFS(int L){
Queue<Integer> Q = new LinkedList<>();
Q.offer(L);
ch_B[L]=1;
sb_B.append(L).append(" ");
while(!Q.isEmpty()){
int V = Q.poll();
for(int i=1;i<=N;i++){
if(graph[V][i]==1 && ch_B[i]==0){
Q.offer(i);
ch_B[i]=1;
sb_B.append(i).append(" ");
}
}
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine()," ");
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
V = Integer.parseInt(st.nextToken());
graph= new int[N+1][N+1];
ch_D= new int[N+1];
ch_B = new int[N+1];
for(int i=0;i<M;i++){
st= new StringTokenizer(br.readLine()," ");
int x = Integer.parseInt(st.nextToken());
int y = Integer.parseInt(st.nextToken());
graph[x][y]=graph[y][x]=1;
}
ch_D[V]=1;
sb_D.append(V).append(" ");
DFS(V);
BFS(V);
bw.write(sb_D.toString()+"\n");
bw.write(sb_B.toString());
bw.flush();
bw.close();
br.close();
}
}응용문제 백준의 14500번
을 풀어보자.
일단 이 문제를 보면 DFS로 풀어야 하는 문제인 것을 확인할 수 있다. 한점을 고정하고 그 점에서 만들 수 있는 모든 도형들을 만들어보는 것이다. 그렇게 전체 배열을 다 돌아서 최대 수를 찾는 것이다.
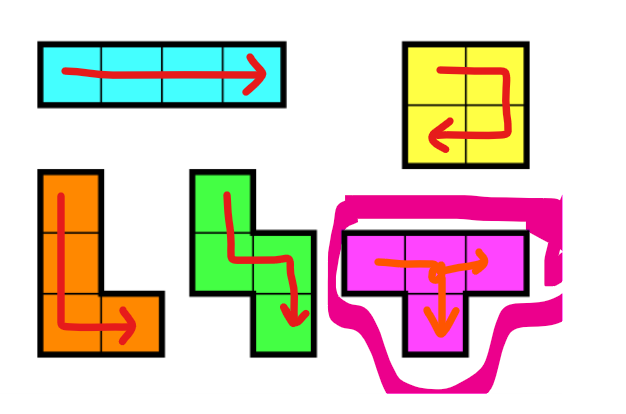
한점에서 상하좌우로 이동가능하도록 설정하여 모든 경로를 탐색하면 된다. 탐색하되 그 개수가 4개로 정해져 있어서 4개가 되는 순간 가장 큰 수와 비교해서 max값보다 크면 max값을 갱신한다. 이 부분은 DFS로 접근이 가능하다.
한가지 더 제약조건이 있다면 돌고나서 꼭 방문한 지점에 대해서 0으로 반환해야 한다. 그래야 다른 모양으로 전환할 때 그 지점에 갈 수 있다.(백트래킹)
그러나 아래 ㅜ모양은 DFS로 불가능하다. 따라서 저 부분은 함수로 따로 빼서 진행하기로 한다.
static void checkShape(int x, int y){
int sum=0;
if( y+2<M && x+1<N){//ㅜ
sum=arr[x][y]+arr[x][y+1]+arr[x][y+2]+arr[x+1][y+1];
if(max<sum) max =sum;
}
if(x-1>=0&&y+1<M&&x+1<N){//ㅓ
sum=arr[x][y]+arr[x][y+1]+arr[x-1][y+1]+arr[x+1][y+1];
if(max<sum) max =sum;
}
if( y+2<M && x-1>=0){//ㅗ
sum=arr[x][y]+arr[x][y+1]+arr[x][y+2]+arr[x-1][y+1];
if(max<sum) max =sum;
}
if(y+1<M && x-1>=0 && x+1<N){//ㅏ
sum=arr[x][y]+arr[x][y+1]+arr[x-1][y]+arr[x+1][y];
if(max<sum) max =sum;
}
}한 점을 받고 나서 그 지점에서 만들 수 있는 ㅜ,ㅓ,ㅗ,ㅜ를 모두 만들어 보는 것이다.
따라서 전체 풀이는 아래와 같다.
import java.util.*;
import java.io.*;
public class Main{
static int[][] arr;
static int[][] ch;
static int N;
static int M;
static int max = Integer.MIN_VALUE;
static int[] cx={0,0,-1,1};
static int[] cy={1,-1,0,0};
static void DFS(int x, int y, int sum, int cnt){
if(cnt==4){
if(sum>max) max=sum;
}else{
for(int i=0;i<4;i++){
int cxx = x + cx[i];
int cyy = y + cy[i];
if(cxx>=N || cxx<0 || cyy>=M || cyy<0) {
continue;
} if(ch[cxx][cyy]==0) {
ch[cxx][cyy] = 1;
DFS(cxx, cyy, sum + arr[cxx][cyy], cnt + 1);
ch[cxx][cyy] = 0;
}
}
}
}
static void checkShape(int x, int y){
int sum=0;
if( y+2<M && x+1<N){
sum=arr[x][y]+arr[x][y+1]+arr[x][y+2]+arr[x+1][y+1];
if(max<sum) max =sum;
}
if(x-1>=0&&y+1<M&&x+1<N){
sum=arr[x][y]+arr[x][y+1]+arr[x-1][y+1]+arr[x+1][y+1];
if(max<sum) max =sum;
}
if( y+2<M && x-1>=0){
sum=arr[x][y]+arr[x][y+1]+arr[x][y+2]+arr[x-1][y+1];
if(max<sum) max =sum;
}
if(y+1<M && x-1>=0 && x+1<N){
sum=arr[x][y]+arr[x][y+1]+arr[x-1][y]+arr[x+1][y];
if(max<sum) max =sum;
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine()," ");
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
arr = new int[N][M];
ch = new int[N][M];
for(int i=0;i<N;i++){
st = new StringTokenizer(br.readLine()," ");
for(int j=0;j<M;j++){
arr[i][j]=Integer.parseInt(st.nextToken());
}
}
for(int i=0;i<N;i++){
for(int j=0;j<M;j++){
ch[i][j]=1;
DFS(i,j,arr[i][j],1);
ch[i][j]=0;
checkShape(i,j);
}
}
bw.write(Integer.toString(max));
bw.flush();
bw.close();
br.close();
}
}