
오늘의 나는 무엇을 잘했을까?
알고리즘 문제를 이미 배운 개념들을 적극적으로 활용하여 풀었다. 개념을 배우고 실전에 적용해보니까 기억에도 오래 남을 것 같고 앞으로 문제푸는데 나만의 가이드라인이 잡혀가는 것 같다.
오늘의 나는 무엇을 배웠을까?
괄호 짝 확인하기 스택 활용 문제
-
실습 설명
마이크로하드에서 일하는 영훈이는 워드 프로세서 팀의 개발자로 일하고 있습니다. 어느날 샘 게이츠 사장님은 영훈이에게 워드 프로세서에서 이용자가 작성한 글에 짝이 없는 모든 괄호를 찾아내서 이용자에게 출력할 수 있는 기능을 추가하라는 특명을 받았습니다. 이 기능은 함수로 만들어 주라고 하는데요.
함수
parentheses_checker()는 인풋으로 문자열 파라미터string을 받습니다.parentheses_checker()는string안에 있는 모든 짝이 없는 괄호를 찾아내서 이 괄호들이 문자열 어디 위치에 있는지를 출력합니다. 만약 문자열 안에 모든 괄호가 짝이 있으면 함수는 아무 내용도 출력하지 않습니다.스택이란 가장 뒤에 데이터를 추가할 수 있고 가장 마지막 데이터를 삭제할 수 있는 추상 자료형이라고 배웠죠. 한 번 파이썬
deque를 추상 자료형 스택으로 이용해서 이 함수를 작성해 봅시다! -
실습 결과
테스트하는 문자열: (1+2)*(3+5) 테스트하는 문자열: ((3*12)/(41-31)) 테스트하는 문자열: ((1+4)-(3*12)/3 문자열 0 번째 위치에 있는 괄호가 닫히지 않았습니다 테스트하는 문자열: (12-3)*(56/3)) 문자열 13 번째 위치에 있는 닫는 괄호에 맞는 열리는 괄호가 없습니다 테스트하는 문자열: )1+14)/3 문자열 0 번째 위치에 있는 닫는 괄호에 맞는 열리는 괄호가 없습니다 문자열 5 번째 위치에 있는 닫는 괄호에 맞는 열리는 괄호가 없습니다 테스트하는 문자열: (3+15(*3 문자열 5 번째 위치에 있는 괄호가 닫히지 않았습니다 문자열 0 번째 위치에 있는 괄호가 닫히지 않았습니다 -
나의 풀이(로직)
1. 스트링을 돌면서(문자가 나오면 스택에 push한다.
2.)문자가 나오면 스택을 확인한다.
3. 스택이 비어있으면 오류(여는 괄호 없이 닫는 괄호가 먼저 나왔다는 뜻)
4. 스택이 비어있지 않다면 pop하여 맞는 짝을 없애준다
5. 문자열 순회가 끝나고, 스택이 빌 때까지 pop하면서 닫는 괄호가 없는 여는 괄호들을 처리해준다.- 내 코드
def parentheses_checker(string): """주어진 문자열 인풋의 모든 괄호가 짝이 있는지 확인해주는 메소드""" print(f"테스트하는 문자열: {string}") stack = deque([]) # 사용할 스택 정의 # 여기에 코드를 작성하세요 for i in range(len(string)): if string[i] == "(": stack.append(i) elif string[i] == ")": if stack: _ = stack.pop() else: print(f"문자열 {i} 번째 위치에 있는 닫는 괄호에 맞는 열리는 괄호가 없습니다") while stack: i = stack.pop() print(f"문자열 {i} 번째 위치에 있는 괄호가 닫히지 않았습니다")
딕셔너리
key-value 쌍을 저장하는 추상 자료형
- key를 이용한 데이터 탐색
- key를 이용한 데이터 삭제
- 데이터간 순서 관계를 약속하지 않음파이썬의 딕셔너리는 해시 테이블로 구현되어 있고, 다음과 같이 사용할 수 있다.
grades = {} # 딕셔너리 생성 # key-value 데이터 삽입 grades["현승"] = 80 grades["태호"] = 60 grades["영훈"] = 90 grades["지웅"] = 70 grades["동욱"] = 96 # 딕셔너리 출력 print(grades) # 값 update grades["태호"] = 100 # key를 이용한 탐색 print(grades["동욱"]) # key를 이용한 삭제 grades.pop("태호") grades.pop("지웅")
Set
Set는 중복을 허용하지 않는 데이터들을 저장하는 추상 자료형
-
삽입: 데이터를 저장(중복 허용하지 않음)
-
탐색: 데이터가 set에 저장되어 있는지 확인할 수 있다
-
삭제: 저장한 데이터를 지울 수 있다
-
데이터간 순서 관계를 약속하지 않는다
파이썬의 set은 다음과 같이 사용한다.
finished_class = set() # 데이터 저장 finished_class.add("자료 구조") finished_class.add("알고리즘") finished_class.add("프로그래밍 기초") finished_class.add("인터랙티브 웹") finished_class.add("데이터 사이언스") print(finished_class) # 데이터 탐색 print("컴퓨터 개론" in finished_class) # False print("자료 구조" in finished_class) # True # 데이터 삭제 finished_class.remove("자료 구조") finished_class.remove("알고리즘")
-
set의 구현
set은 보통 해시테이블을 이용하여 구현한다. 데이터를 저장할 때 처음부터 key만 저장하면, 중복을 허용하지 않고 데이터를 저장할 수 있다. value를 저장하지 않아도 아무 문제가 없다. 탐색, 삭제, 삽입 등은 key를 가지고 하는 연산이므로 이 역시 문제가 없다.
삼송전자 주식 분석 알고리즘 문제
-
문제 설명
태호는 주식 분석이 취미입니다.
요즘 제일 핫한 종목은 삼송전자인데요. 삼송전자의 주식을 딱 한 번 사고 팔았다면 최대 얼마의 수익이 가능했을지 궁금합니다. 그것을 계산해 주는 함수
max_profit()을 작성하세요.max_profit()은 파라미터로 일별 주식 가격이 들어 있는 리스트stock_prices를 받고 최대 수익을 리턴합니다. 주식은 딱 한 번만 사고 한 번만 팝니다. 그리고 사는 당일에 팔 수는 없습니다.하나의 예시로, 지난 6일간 삼송전자의 주식 가격이 이렇다고 가정합시다.
max_profit([7, 1, 5, 3, 6, 4])이 기간 동안 낼 수 있는 최대 수익은 얼마일까요? 둘째 날 11에 사서 다섯째 날 66에 팔면 총 55의 수익이 생깁니다.
또 다른 예시를 봅시다.
max_profit([7, 6, 4, 3, 1])이 기간 동안 가능한 최대 수익은 얼마일까요? 이번에는 주식이 계속 떨어지기만 하네요. 하지만 꼭 한 번은 사고 팔아야 하기 때문에, 첫 날 77에 사고 둘째 날 66에 팔아서 나오는 −1−1이 최대 수익입니다.
-
나의 풀이 1 - 재귀함수 활용
-
base case
- stock_list길이가 3 : 가능한 3가지 경우에 대해 max값 리턴
- 길이가 2: stock_list[1] - stock_list[0] 리턴
- 길이가 1 이하: 0 리턴
-
로직
- 배열을 반으로 나누어 왼쪽에서 min값(가장 싸게 산 가격)과 오른쪽에서 max값의 차이를 구한다(가장 비싸게 판 가격) - 이 차익을 profit이라 한다
- 배열의 오른쪽에서 가능한 max, 1번에서 구한 profit, 배열의 왼쪽에서 가능한 max중 max값을 리턴한다.
-
코드
def max_profit(stock_list): if len(stock_list) == 3: case_1 = stock_list[1] - stock_list[0] case_2 = stock_list[2] - stock_list[0] case_3 = stock_list[2] - stock_list[1] return max(case_1, case_2, case_3) if len(stock_list) == 2: return stock_list[1] - stock_list[0] if len(stock_list) <= 1: return 0 mid = len(stock_list) // 2 left = stock_list[:mid] right = stock_list[mid:] profit = max(right) - min(left) return max(profit, max_profit(left), max_profit(right))- 문제점
- 문제에서 요구한 으로 풀지 못한다.
- 문제점
-
-
모범 답안 -
-
로직
- 리스트를 순회하며 지금까지 나온 가장 작은 값(제일 싼 가격)을 계속 갱신한다.
- 지금까지 최대 수익 = max(지금까지 최대 수익, 현재 가격 - 기억하는 가장 싼 가격)
- 반복문이 종료되면 지금까지 최대수익이 전체 최대수익으로 갱신되어 있다.
-
코드
def max_profit(stock_list): # 여기에 코드를 작성하세요 min_so_far = stock_list[0] max_profit_so_far = stock_list[1] - stock_list[0] for i in range(1, len(stock_list)): max_profit_so_far = max(max_profit_so_far, stock_list[i] - min_so_far) min_so_far = min(min_so_far, stock_list[i]) return max_profit_so_far
-
출근하는 방법1 알고리즘 문제
-
실습 설명
영훈이는 출근할 때 계단을 통해 사무실로 가는데요. 급할 때는 두 계단씩 올라가고 여유 있을 때는 한 계단씩 올라 갑니다.
어느 날 문득, 호기심이 생겼습니다. 한 계단 또는 두 계단씩 올라가서 끝까지 올라가는 방법은 총 몇 가지가 있을까요?
계단 4개를 올라간다고 가정하면, 이런 방법들이 있습니다.
1, 1, 1, 1
2, 1, 1
1, 2, 1
1, 1, 2
2, 2총 5개 방법이 있네요.
함수
staircase()는 파라미터로 계단 수n을 받고, 올라갈 수 있는 방법의 수를 효율적으로 찾아서 리턴합니다.print(staircase(0)) # => 1 print(staircase(1)) # => 1 print(staircase(4)) # => 5 -
나의 풀이 ()
-
로직
- n번째 계단으로 올라올 수 있는 경우는 n-1번째에서 1칸, n-2번째에서 2칸 올라오는 경우로 나눌 수 있다.
- 점화식으로 표현하면 case(n) = case(n - 1) + case(n - 2)이다.
- dp알고리즘의 tabulation 기법을 사용하여 bottom-up방식으로 case(n)을 찾는다.
-
코드
def staircase(n): # 여기에 코드를 작성하세요 dp = [0,1,2] if n <= 2: return dp[n] dp.extend([0] * (n-2)) for i in range(3, n+1): dp[i] = dp[i - 1] + dp[i - 2] return dp[n] -
답이 틀렸다고 나온다. 알고 보니 staircase(0)은 1이 나와야 한다고 한다..
-
출근하는 방법2 알고리즘 문제
-
실습 설명
영훈이는 출근할 때 계단을 통해 사무실로 가는데요. 급할 때는 두 계단씩 올라가고 여유 있을 때는 한 계단씩 올라갑니다. 결국 계단을 오를 수 있는 모든 방법으로 계단을 올라갔는데요.
이제 다르게 계단을 올라갈 수는 없을까 고민하던 영훈이는 특이한 방법으로 계단을 오르려고 합니다.
가령 계단을 한 번에 1, 2, 4 칸씩 올라가 보는 건데요. 예를 들어서 계단을 4개를 올라가야 되면:
1, 1, 1, 1
2, 1, 1
1, 2, 1
1, 1, 2
2, 2
4총 6개 방법이 있네요.
함수
staircase()는 파라미터로 총 계단 수n그리고 한 번에 올라갈 수 있는 계단 수를possible_steps로 받고, 올라갈 수 있는 방법의 수를 효율적으로 찾아서 리턴합니다.그러니까
n이3,possible_steps가[1, 2, 3]이면, 계단 총 3칸을 1, 2, 3칸씩 갈 수 있을 때 오르는 방법의 수를 구하는 거죠. 단,possible_steps에는 항상1이 포함된다고 가정합니다. -
나의 풀이 ()
-
로직
- 출근하는 방법 1과 마찬가지로 점화식을 세운다
- case(n) = case(n-ps[0]) + case(n-ps[1]) + …
- 이 때, ps[j]가 n보다 크면 0을 더한다. (4칸 올라가는 경우의 수를 구하는데 ps에 5칸이 있다면 5칸을 올라와 4칸만큼 가는 경우는 없기 때문에)
-
코드
# 높이 n개의 계단을 올라가는 방법을 리턴한다 def staircase(n, possible_steps): # 여기에 코드를 작성하세요 dp = [1, 1] if n <= 1: return dp[n] dp.extend([0] * (n - 1)) for i in range(2, n+1): for step in possible_steps: dp[i] += dp[i-step] if step <= i else 0 return dp[n]
-
트리
트리란 데이터간에 계층적 관계가 있을 때 데이터 자체와 더불어 계층적 관계를 함께 저장할 수 있는 자료구조이다. 트리는 링크드 리스트와 마찬가지로 데이터가 노드 형태로 저장된다. 노드는 다음과 같이 자식 노드에 대한 레퍼런스를 가진다.
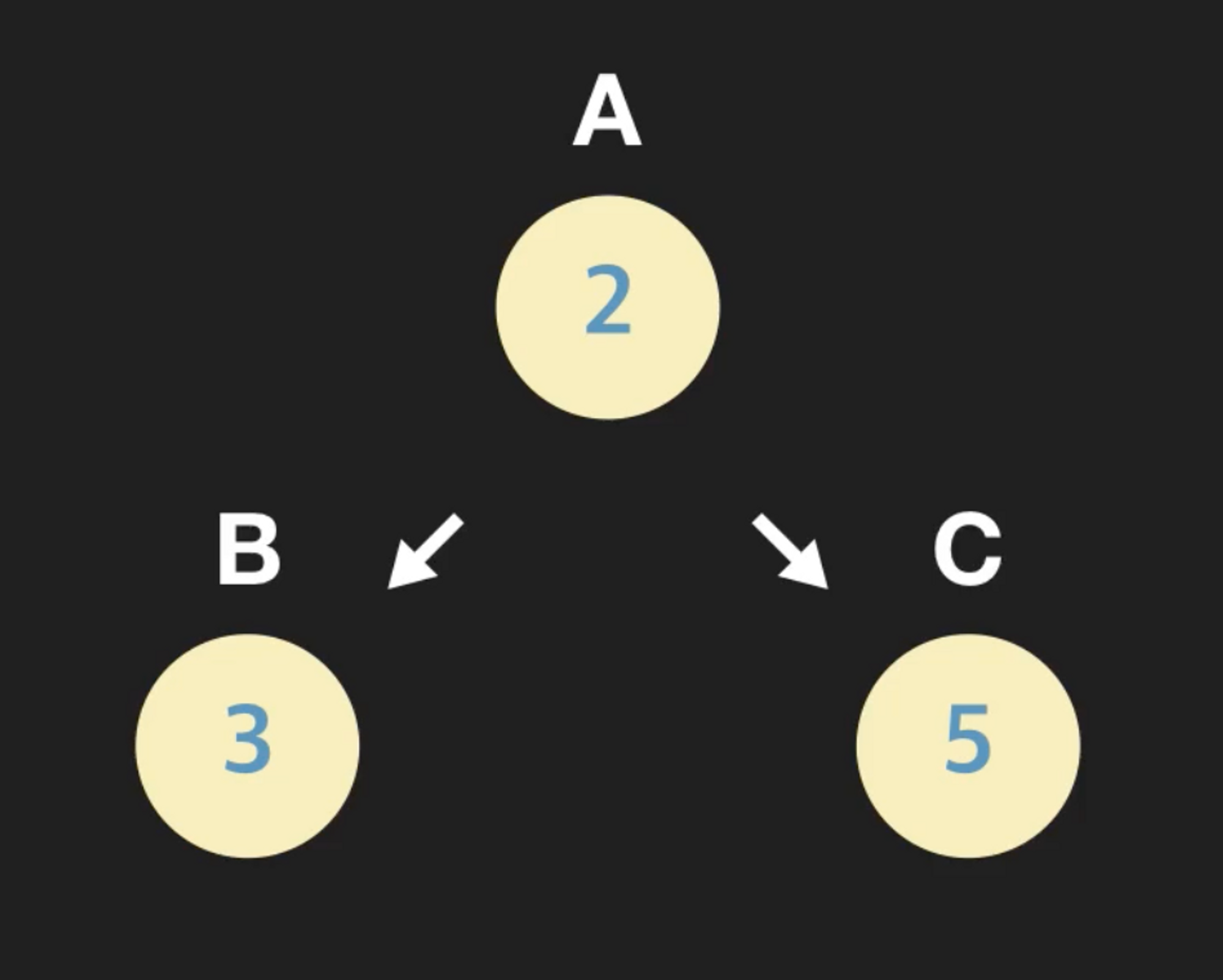
- 트리 관련 용어 정리
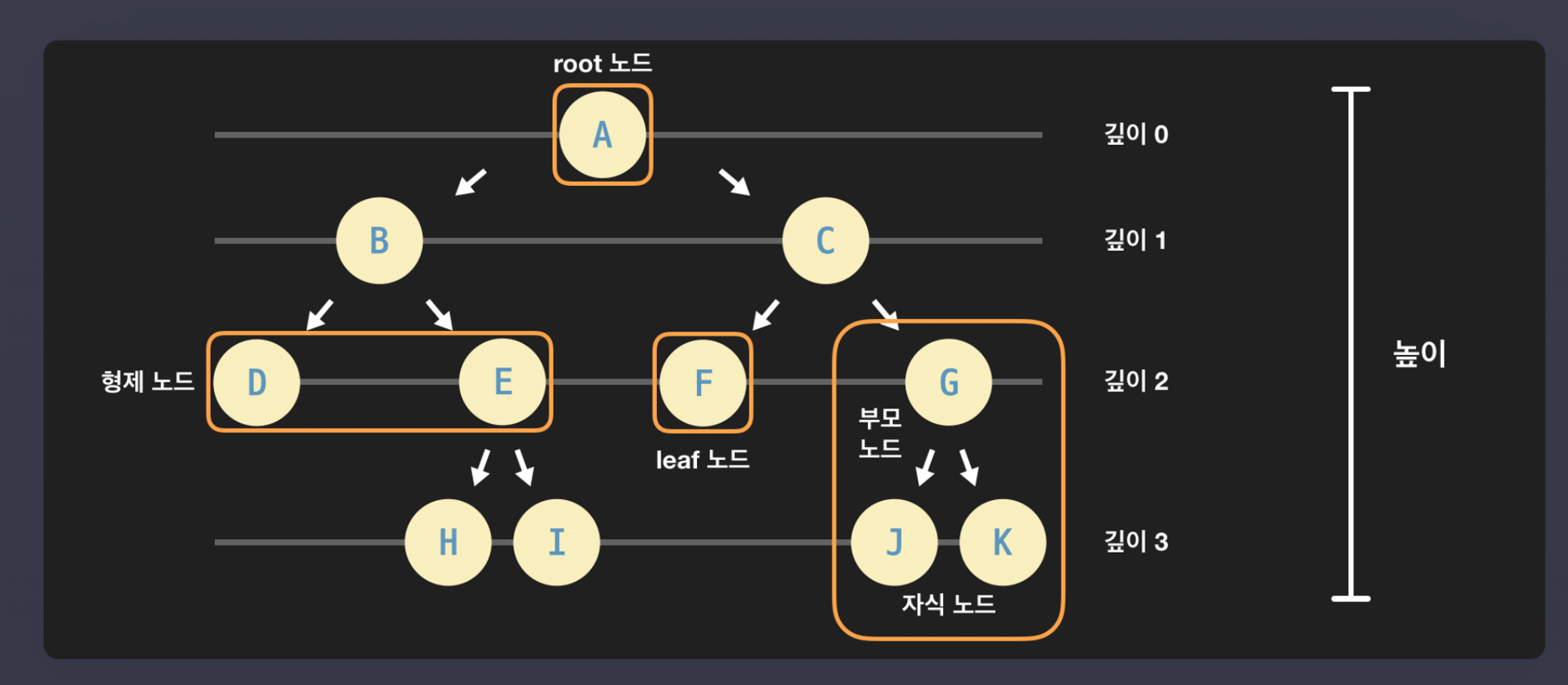
- 트리의 활용
- 계층적 관계가 있는 자료들을 자연스럽게 저장할 수 있다
- 컴퓨터 과학의 다양한 문제들을 기발하게 해결할 수 있다(정렬, 압축 등)
- 다양한 추상 자료형을 구현할 수 있다
이진 트리
각 노드마다 자식 노드를 2개 이하만 가지는 트리
-
구현
아래의 트리를 만들어 본다.
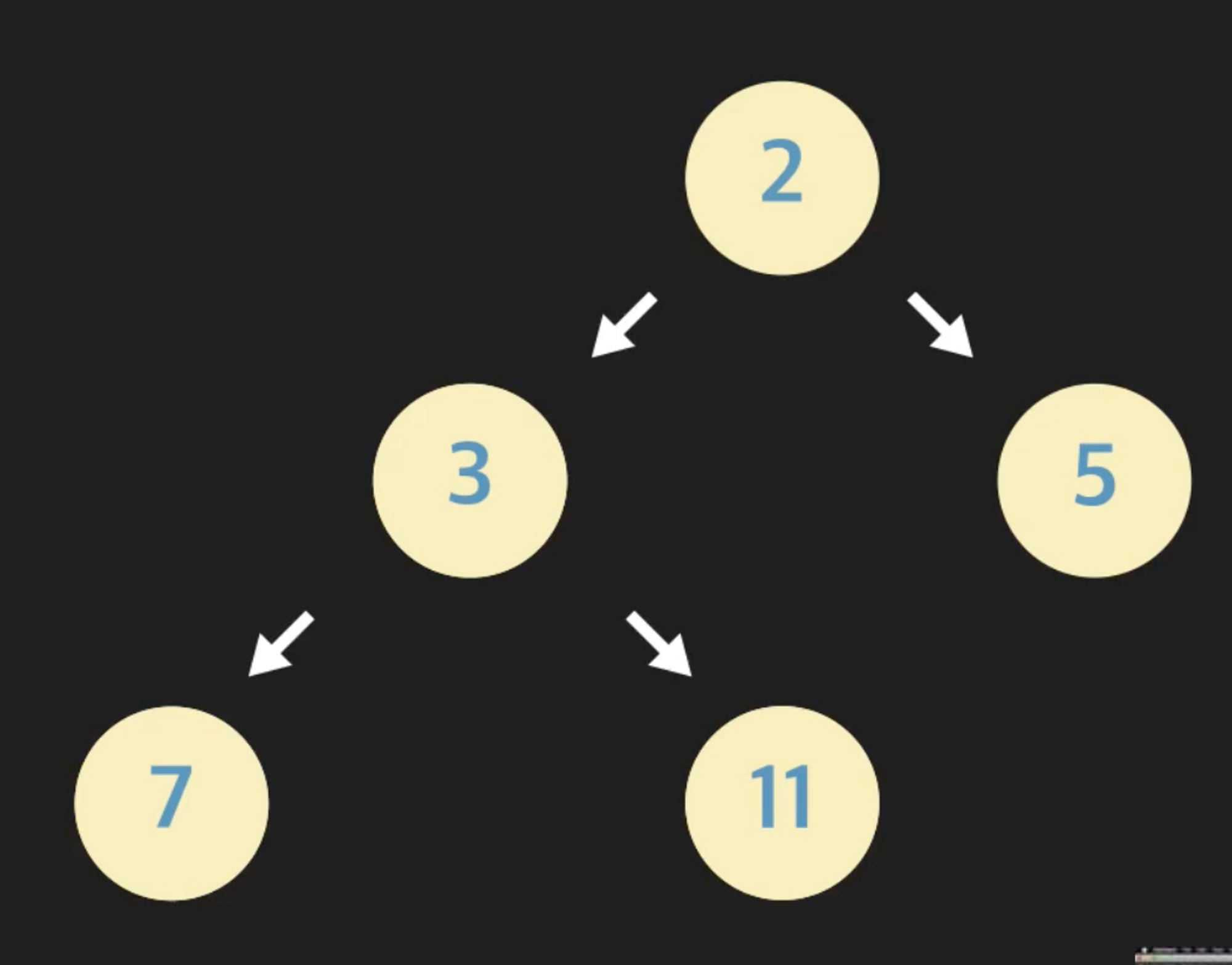
class Node: def __init__(self, data): self.data = data self.left_child = None self.right_child = None # 노드 인스턴스 생성 root_node = Node(2) node_B = Node(3) node_C = Node(5) node_D = Node(7) node_E = Node(11) # B와 C노드를 루트 노드의 자식으로 지정 root_node.left_child = node_B root_node.right_child = node_C # D와 E를 B노드의 자식으로 지정 node_B.left_child = node_D node_B.right_child = node_E -
이진 트리 종류
- Full Binary Tree (정 이진트리)
-
모든 노드가 0개 혹은 2개의 자식을 갖는 트리
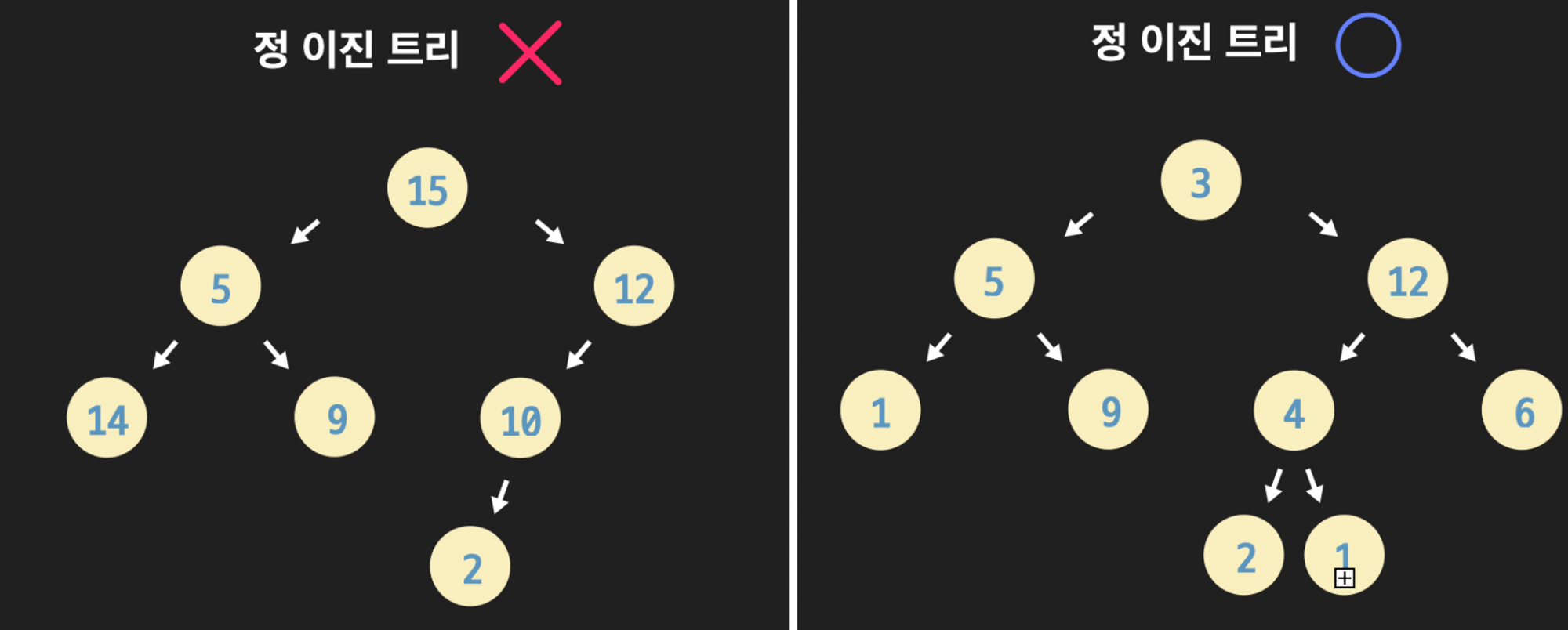
-
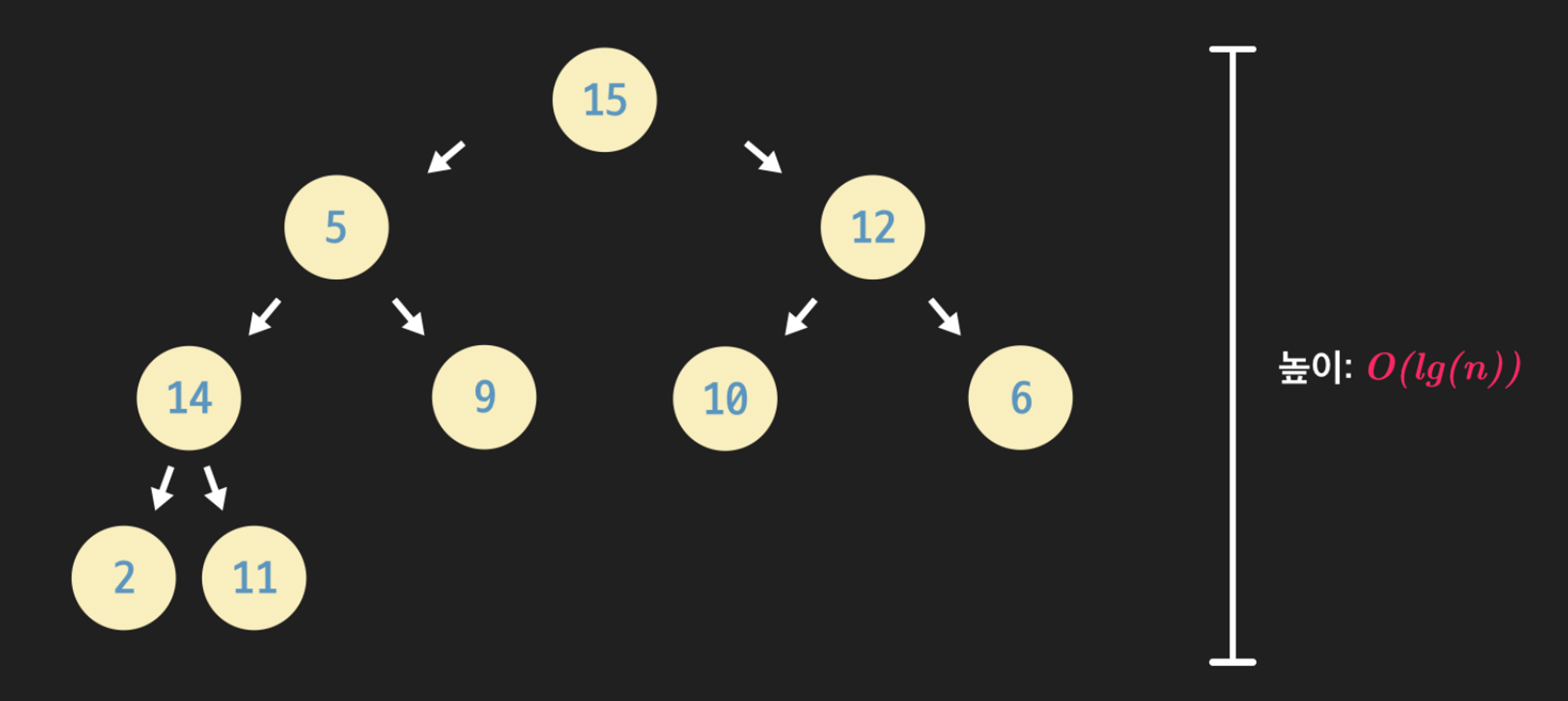
- Complete Binary Tree (완전 이진트리)
-
마지막을 레벨을 제외한 모든 레벨이 꽉 차있고, 마지막 레벨은 왼쪽 부터 오른쪽 방향으로 차 있는 트리
-
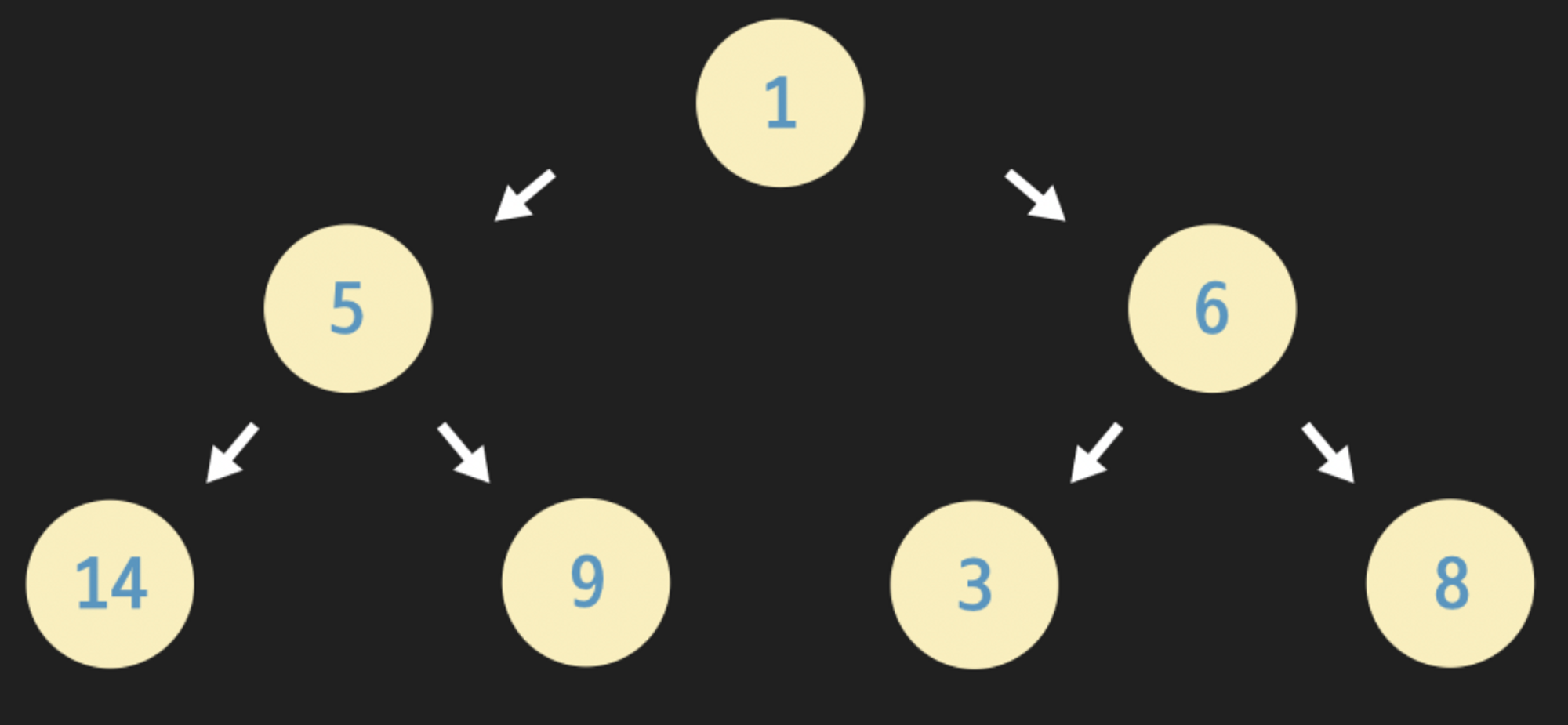
- Perfect Binary Tree (포화 이진트리)
-
모든 레벨이 빠짐없이 다 노드로 채워져있는 이진 트리
-
- Full Binary Tree (정 이진트리)
-
완전 이진 트리 구현
-
배열로 표현한 완전 이진 트리의 기능들을 구현해본다.
-
get_parent_index: 부모 노드의 인덱스 리턴
-
get_left_child_index: 왼쪽 자식 인덱스 리턴
-
get_right_child_index: 오른쪽 자식 인덱스 리턴
def get_parent_index(complete_binary_tree, index): """배열로 구현한 완전 이진 트리에서 index번째 노드의 부모 노드의 인덱스를 리턴하는 함수""" # 여기에 코드를 작성하세요 if index == 1: return None return index // 2 if complete_binary_tree[index // 2] is not None else None def get_left_child_index(complete_binary_tree, index): """배열로 구현한 완전 이진 트리에서 index번째 노드의 왼쪽 자식 노드의 인덱스를 리턴하는 함수""" # 여기에 코드를 작성하세요 try: if complete_binary_tree[index * 2]: return index * 2 except: return None def get_right_child_index(complete_binary_tree, index): """배열로 구현한 완전 이진 트리에서 index번째 노드의 오른쪽 자식 노드의 인덱스를 리턴하는 함수""" # 여기에 코드를 작성하세요 try: if complete_binary_tree[index * 2 + 1]: return index * 2 + 1 except: return None
-
트리 순회
정의: 트리를 순회하며 모든 데이터를 한 번씩 거쳐가는 것
호출: traverse(root_node)
트리 순회에는 다음과 같이 3가지 방법이 있다.
- pre-order traverse : node → left_child_tree → right_child_tree순으로 순회
- post-order traverse: left_child_tree, right_child_tree, node순으로 순회
- in-order traverse: left_child_tree, node, right_child_tree순으로 순회
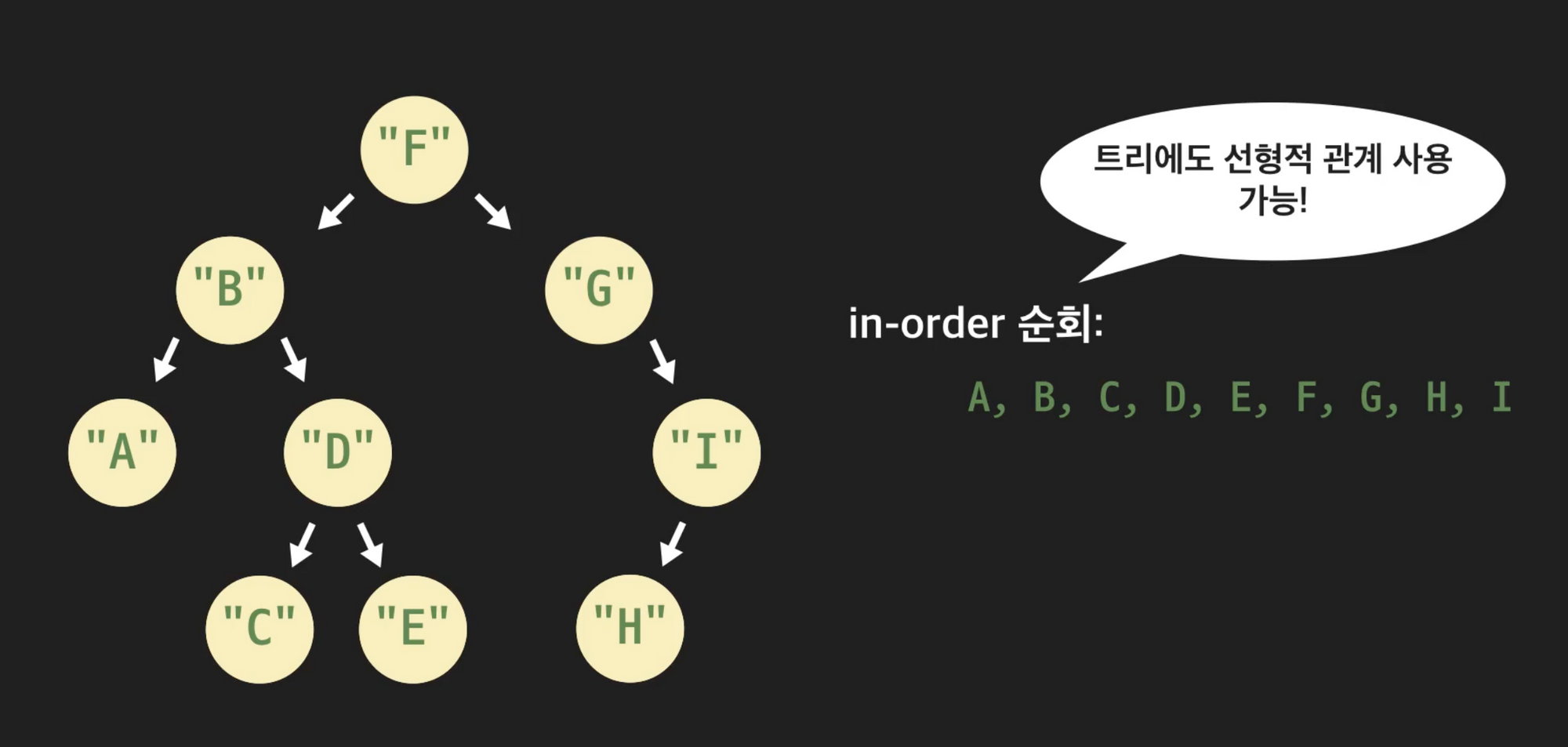
순회 방식에 따라 각 노드의 방문 순서가 달라지며, 저장된 구조에 따라 선형적인 관계또한 사용가능하다. 예를 들어 다음과 같은 트리를 in-order방식으로 순회하면 알파벳 순서대로 노드를 방문하게 된다.
힙 (heap)
다음은 힙의 조건이자 속성이다.
- 완전 이진트리이다.
- 모든 노드의 데이터는 자식 노드들의 데이터보다 크거나 같다.
힙의 특성을 이용하면 정렬문제를 효율적으로 풀 수 있다. 정렬되지 않은 데이터들을 완전 이진 트리 형태로 저장 후 해당 트리를 힙으로 만드는 것을 통해 시간 복잡도 로 정렬할 수 있다.
- heapify 함수
-
완전 이진 트리에 속한 하나의 노드에 대해서 힙 속성을 지키도록 자식들과 비교하며 자기 자신의 위치를 변경하는 함수
-
-
코드
def swap(tree, index_1, index_2): """완전 이진 트리의 노드 index_1과 노드 index_2의 위치를 바꿔준다""" temp = tree[index_1] tree[index_1] = tree[index_2] tree[index_2] = temp def heapify(tree, index, tree_size): """heapify 함수""" def get_max_index(i, l_i, r_i): _max = (i, tree[i]) for index in [l_i, r_i]: if tree[index] > _max[1]: _max = (index, tree[index]) return _max[0] # 왼쪽 자식 노드의 인덱스와 오른쪽 자식 노드의 인덱스를 계산 left_child_index = 2 * index right_child_index = 2 * index + 1 # 여기에 코드를 작성하세요 while True: if left_child_index > tree_size-1: #자식이 없음 break elif right_child_index > tree_size-1: # 왼쪽 자식만 있음 if tree[index] > tree[left_child_index]: swap(tree, index, left_child_index) break else: max_index = get_max_index(index, left_child_index, right_child_index) if max_index == index: break swap(tree, index, max_index) index = max_index left_child_index = index * 2 right_child_index = index * 2 + 1
-
- 힙 만들기
- tree배열의 끝 인덱스부터 루트 인덱스까지 heapify 호출하면, 전체 트리가 힙이 되어 있다.
- 힙 정렬(heap sort)
-
힙을 만든다
-
root와 마지막 노드를 바꾼다
-
바꾼 노드는 없는 인덱스 취급을 한다
-
새로운 노드가 힙 속성을 지킬 수 있게(자리를 찾을 수 있게) heapify를 호출한다
def swap(tree, index_1, index_2): """완전 이진 트리의 노드 index_1과 노드 index_2의 위치를 바꿔준다""" temp = tree[index_1] tree[index_1] = tree[index_2] tree[index_2] = temp def heapify(tree, index, tree_size): """heapify 함수""" # 왼쪽 자식 노드의 인덱스와 오른쪽 자식 노드의 인덱스를 계산 left_child_index = 2 * index right_child_index = 2 * index + 1 largest = index # 일단 부모 노드의 값이 가장 크다고 설정 # 왼쪽 자식 노드의 값과 비교 if 0 < left_child_index < tree_size and tree[largest] < tree[left_child_index]: largest = left_child_index # 오른쪽 자식 노드의 값과 비교 if 0 < right_child_index < tree_size and tree[largest] < tree[right_child_index]: largest = right_child_index if largest != index: # 부모 노드의 값이 자식 노드의 값보다 작으면 swap(tree, index, largest) # 부모 노드와 최댓값을 가진 자식 노드의 위치를 바꿔준다 heapify(tree, largest, tree_size) # 자리가 바뀌어 자식 노드가 된 기존의 부모 노드를대상으로 또 heapify 함수를 호출한다 def heapsort(tree): """힙 정렬 함수""" tree_size = len(tree) # 힙으로 만들기 for i in range(tree_size-1, 0, -1): heapify(tree, i, tree_size) # 마지막 노드부터 순서대로 루트노드와 맞바꾼뒤 heapify for i in range(1, tree_size-1): # print(tree_size- i) swap(tree, 1, tree_size - i) heapify(tree, 1, tree_size - i)
-
- 힙으로 구현하는 우선순위 큐
- 추상 자료형
- 저장한 데이터가 우선순위 순서대로 나온다
- 힙에 데이터 삽입 과정(맥스 힙 기준)
-
힙에 마지막 인덱스에 데이터를 삽입한다
-
삽입한 데이터와 부모 노드의 데이터를 비교한다
-
부모 노드의 데이터가 더 작으면 둘의 위치를 바꿔준다
-
새로 삽입한 노드가 제 위치를 찾을 때까지 반복한다
def reverse_heapify(tree, index): """삽입된 노드를 힙 속성을 지키는 위치로 이동시키는 함수""" parent_index = index // 2 # 삽입된 노드의 부모 노드의 인덱스 계산 # 여기에 코드를 작성하세요 while True: if index <= 1: # 루트 노드인 경우(부모 노드가 없는 경우) break else: if tree[index] > tree[parent_index]: swap(tree, index, parent_index) index = parent_index parent_index //= 2 class PriorityQueue: """힙으로 구현한 우선순위 큐""" def __init__(self): self.heap = [None] # 파이썬 리스트로 구현한 힙 def insert(self, data): """삽입 메소드""" # 여기에 코드를 작성하세요 self.heap.append(data) index = len(self.heap) - 1 reverse_heapify(self.heap, index)
-
오늘의 나는 어떤 어려움이 있었을까?
- 알고리즘 문제를 푸는데 고전했다. 아직 많은 연습이 필요한 것 같다. 특히 힌트나 비슷한 유형의 문제를 푼 경험이 없을 때 완전히 나만의 사고력으로 풀이법을 떠올리는 경우가 거의 없었다.
- heapify 실습에서 헷갈린 나머지 시간을 너무 지체했다.
내일의 나는 무엇을 해야할까?
- 알고리즘 문제(문제 해결 능력 기르기 강의) 풀기
- 트리 강의 완강, 그래프 강의 완강
- 위클리 미션 리팩토링 및 PR
