Big O 정리

- Big O 란?

Big O는 알고리즘의 실행 시간을 표현하는 표기법이다.

Big O의 O는 Order의 줄임말인데, 입력 된 크기에 비례해서 해당 코드를 처리하는데 얼마나 많은 시간이 소요되는지 나타내는 용어이다.

빅오 표기법은 최악의 경우의 실행 시간이 나타내는 것이므로, 평균 실행 시간을 의미하는 것은 아니다.

function addUpTo(n) {
  return (n * (n + 1)) / 2;
}

위의 코드는 n이 100000000이라는 큰 숫자가 들어간다고 하더라도 연산은 무조건 한번 이루어지는 것이므로 O(1)이라는 상수 시간 복잡도를 가진다.

function addUpTo(n) {
  let total = 0;
  for (let i = 1; i <= n; i++) {
    total += i;
  }

  return total;
}

위의 경우에는 n이 1이나 10 같은 작은 경우에는 연산 횟수가 작지만,100, 1000, 10000 점점 입력 값이 늘어날수록 연산 횟수도 늘어나기 때문에 O(n)이라는 시간 복잡도를 가진다.

function countUpAndDown(n) {
  console.log("상승");

  for (let i = 0; i < n; i++) {
    console.log(i);
  }

  console.log("꼭대기! 하강");

  for (let j = n - 1; j >= 0; j--) {
    console.log(j);
  }

  console.log("맨 밑 끝!");
}

이런 경우에는 반복문이 한번 실행 된 후에 다시 또 실행되기때문에 O(2n)이라고 생각할수 있는데, 시간 복잡도 계산에서는 이런 계수들 까지 포함시키지 않는다. 이런 경우에는 그냥 O(n)이라고 한다.

function printAllPairs(n) {
  for (let i = 0; i < n; i++) {
    for (let j = q; j < n; j++) {
      console.log(i, j);
    }
  }
}

하지만 이런식으로 이중 반복문 같은 경우에는 i가 1일때 j만큼, 또 i가 +1 되어서 j만큼.. 이런식으로 n * n 만큼 반복문이 실행되므로 이런 경우의 시간 복잡도는 O(n^2)이다.

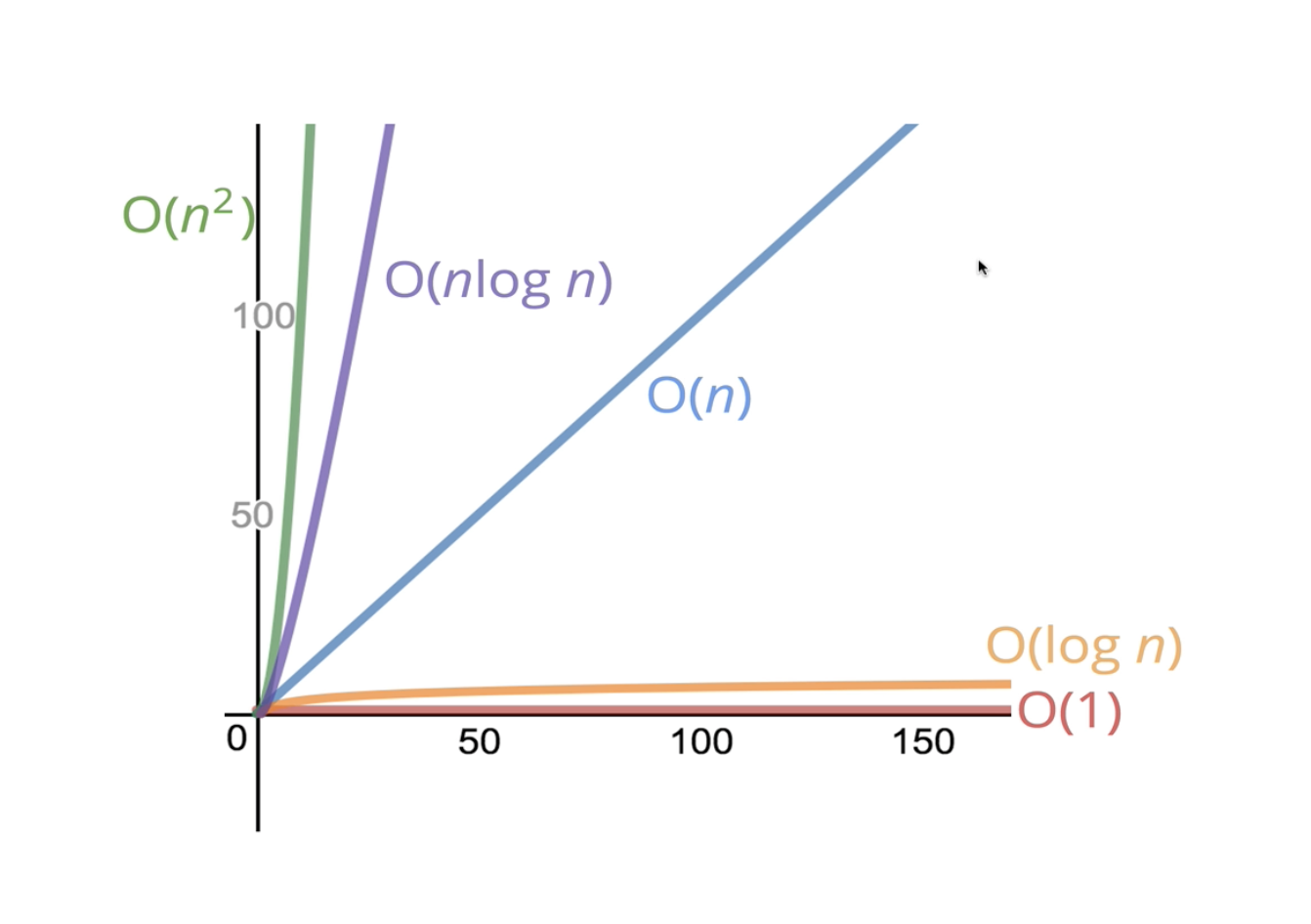
이런식으로 주어진 문제를 해결하는데에 얼마나 많은 시간이 소요되느냐를 측정하는 것이 시간 복잡도이다.

function double(arr) {
  let newArr = [];

  for (let i = 0; i < arr.length; i++) {
    newArr.push(2 * arr[i]);
  }
  return newArr;
}

하지만 위의 코드를 보자.

위의 코드에서 시간 복잡도는 O(n)이며, 배열을 사용하고 있다. 만약에 인풋으로 들어온 arr의 길이가 10개면 newArr도 10일 것이고, arr의 길이가 50이면 newArr 도 50일것이다.

이런 경우에 인풋값에 따라서 결과의 배열 길이도 달라지므로 공간 복잡도도 O(n)이라고 생각한다.