다중 선형 회귀

---

다중 선형회귀 모델

• 2개 이상 특성의 선형회귀

그래프 확인

style.use('seaborn-talk')
fig = plt.figure()

ax = fig.gca(projection='3d')

x = 'GrlivArea'
y = 'OverallQual'
z = 'SalePrice'
ax.scatter(train[x], train[y], train[z]) #2개 특성과 1개 타겟의 3차원 scatter

plt.suptitle('Housing Prices')
plt.show()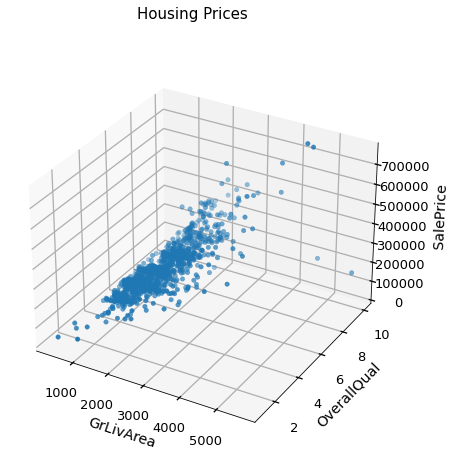

모델 학습

features = ['GrLivArea', 'OverallQual'] #2개 특성
X_train = train[features]
X_test = test[features]

model = LinearRegression()

model.fit(X_train, y_train)
y_pred = model.predict(X_train)
mae = mean_absolute_error(y_train, y_pred)
print(f'훈련 에러: {mae:.2f}')

훈련 에러: 29129.58

계수

model.intercept_, model.coef_

(-102743.02342270731, array([ 54.40145532, 33059.44199506]))

---

회귀 모델 평가 지표

MAE

• 절대값 평균
  $\frac{1}{n}\sum_{i=1}^{n}\left | y_{i} - \hat{y_{i}} \right |$

MSE

• 제곱값 평균
  $\frac{1}{n}\sum_{i=1}^{n}(y_{i} - \hat{y_{i}})^{2}$

RMSE

• MSE 제곱근
  $\sqrt{MSE}$

R-squared

• 결정계수
• 특성의 타겟 설명능력(0~1)
  $1 - \frac{\sum_{i=1}^{n}(y_{i} - \hat{y_{i}})^{2}}{\sum_{i=1}^{n}(y_{i} - \bar{y_{i}})^{2}} = 1 - \frac{SSE}{SST} = \frac {SSR}{SST}$

---

과적합, 과소적합

일반화
- 모든 데이터셋에서의 오차 정도
- val, test에서 좋은 성능을 내는 모델 = 일반화 잘된 모델
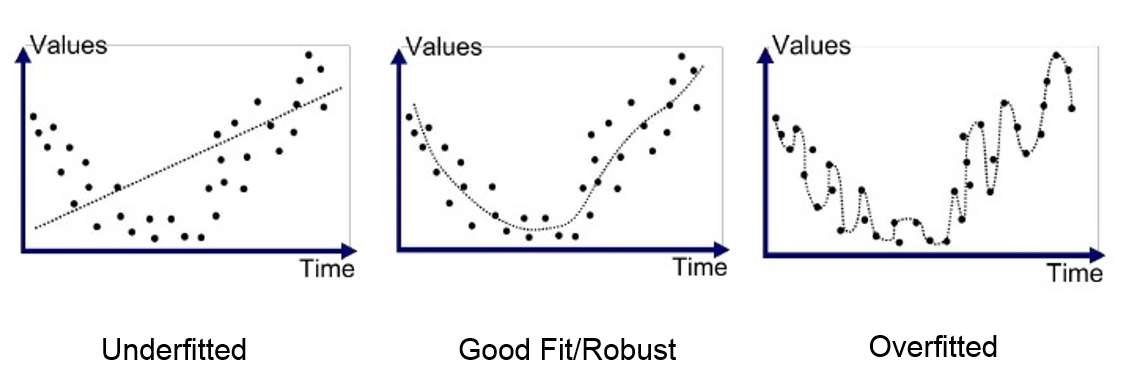
과적합
- 훈련 데이터의 정확도만 높은 상태
과소적합
- 모든 데이터의 정확도가 떨어지는 상태

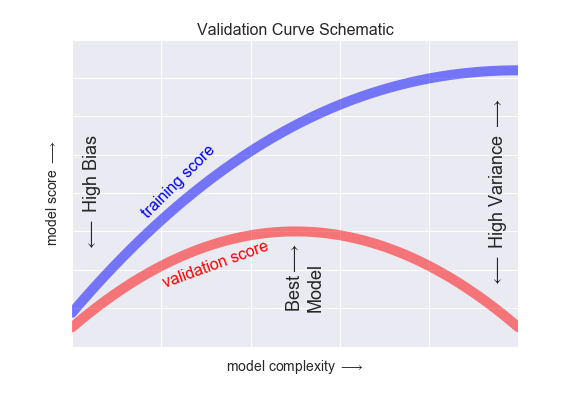
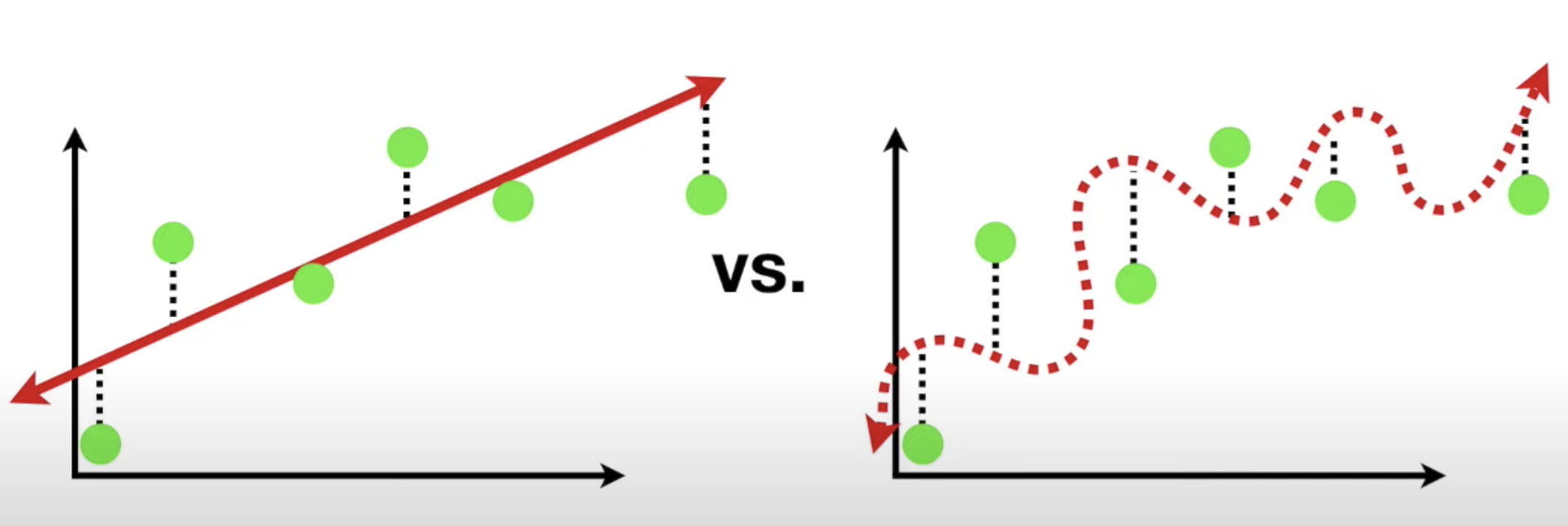
모델의 복잡도가 증가함에 따라 훈련데이터 성능은 증가하고 검증데이터 성능은 특정지점부터 감소
-> 과적합이 발생하는 시점
-> 학습 중지 필요

---

분산, 편향

분산
- 분산이 클 경우 과적합 상태(곡선)
편향
- 편향이 클 경우 과소적합 상태(직선)

---

다항 회귀

• 회귀계수의 차수가 2이상인 회귀 모델

#사용할 임시 데이터
rng = np.random.RandomState(1)
data = np.dot(rng.rand(2, 2), rng.randn(2, 30)).T
X = pd.DataFrame([i[0] for i in data])
y = pd.DataFrame([i[1] for i in data])

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)

#다항 회귀 차수 지정
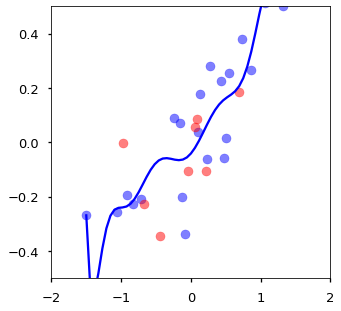
model = PolynomialRegression(3) 

model.fit(X_train, y_train)

plt.scatter(X_train, y_train, color='blue', alpha=0.5)
plt.scatter(X_test, y_test, color='red', alpha=0.5)

x_domain = np.linspace(X.min(), X.max()) #예측 범위
curve = model.predict(x_domain)
plt.plot(x_domain, curve, color='blue')
plt.show()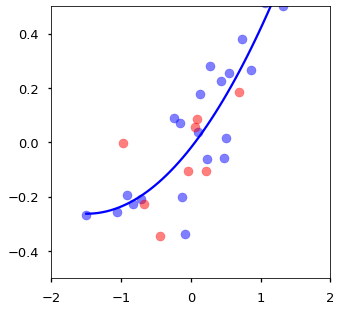

#6차항
model = PolynomialRegression(6)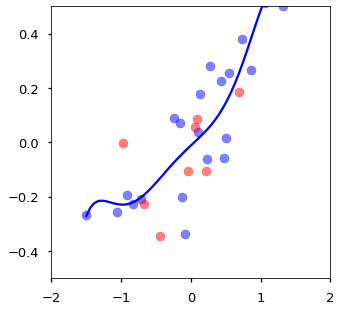 

#10차항
model = PolynomialRegression(10)