데이터를 전송하기 위해서는 전자기 신호로 변환해야 합니다. 이를 위해서는 모두가 이해할 수 있는 디지털 신호나 아날로그 신호를 전자기파 또는 무선파 형태로 변환해야 합니다. 이러한 과정을 변조(Modulation)이라고 합니다.

변조는 전자기파의 특성인 진폭, 주파수, 위상 등을 변화시킴으로써 데이터를 나타냅니다. 예를 들어, 진폭 변조(AM)는 전자기파의 진폭을 변화시켜 데이터를 전송합니다. 주파수 변조(FM)는 전자기파의 주파수를 변화시켜 데이터를 전송합니다.

전자기파로 변조된 데이터는 구리선, 광섬유 케이블, 무선으로 전송됩니다. 수신측에서는 전자기파를 복조하여 원래의 데이터를 추출합니다.

Analog vs Digital signals

• Analog signals : continuous 연속적
• Digital signals : discrete 분리된
  

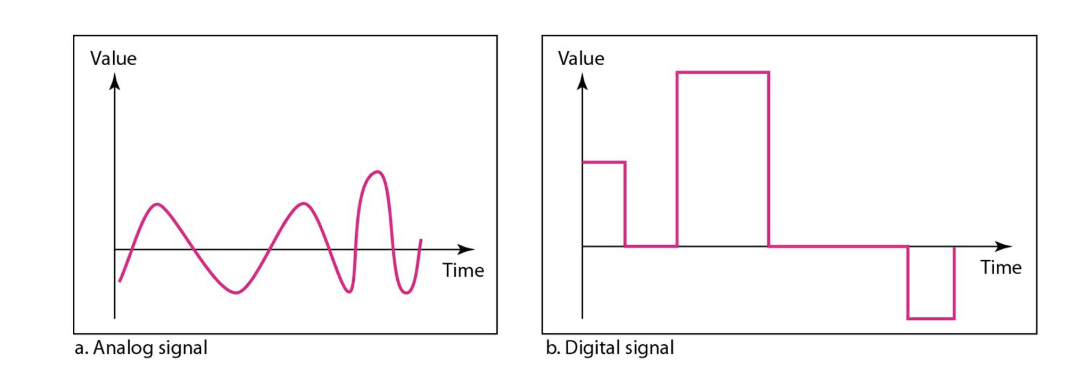
Analog Signal

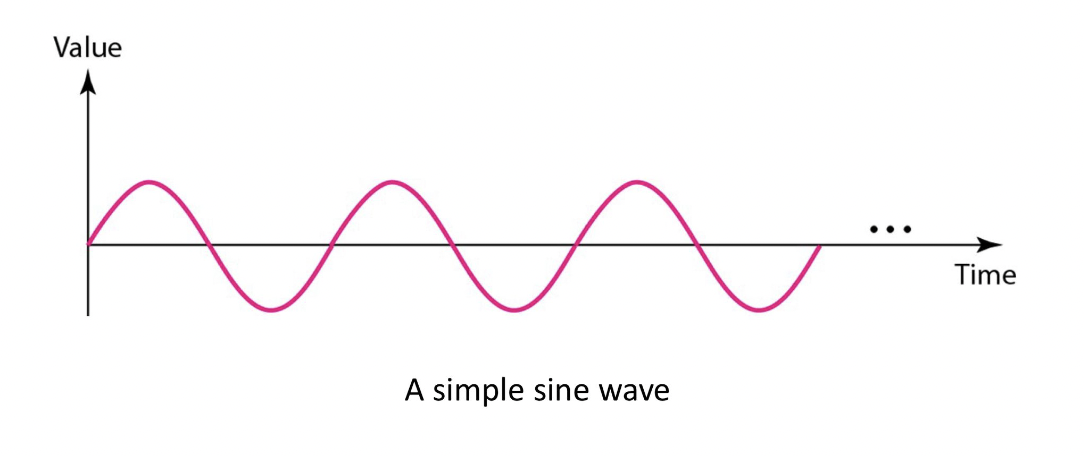
• periodic signal (주기 신호) → 같은 패턴이 반복됨 → sine wave → maximum amplitude 최대 진폭 : 해당 주기에서의 최댓값의 절댓값
  

Frequency & Period

Frequency (f) 주파수(단위 : Hz)

→ How many times does the signal oscillate in a second?

1초에 몇 번 진동하는가?

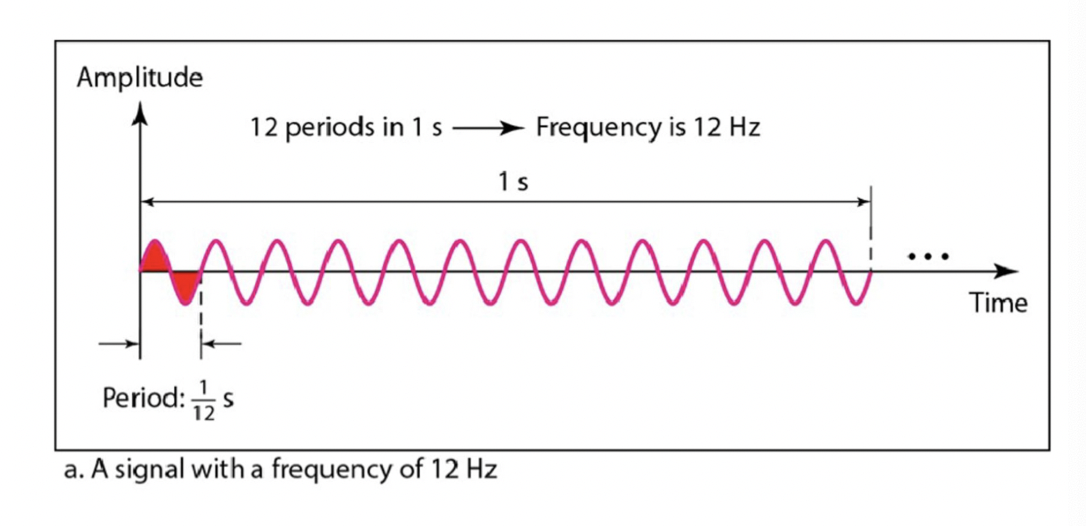
Period (T) 주기 (단위 : s)

→ What is the time that the same pattern restarts?

한 번 출렁이는데 몇 초가 걸리나?

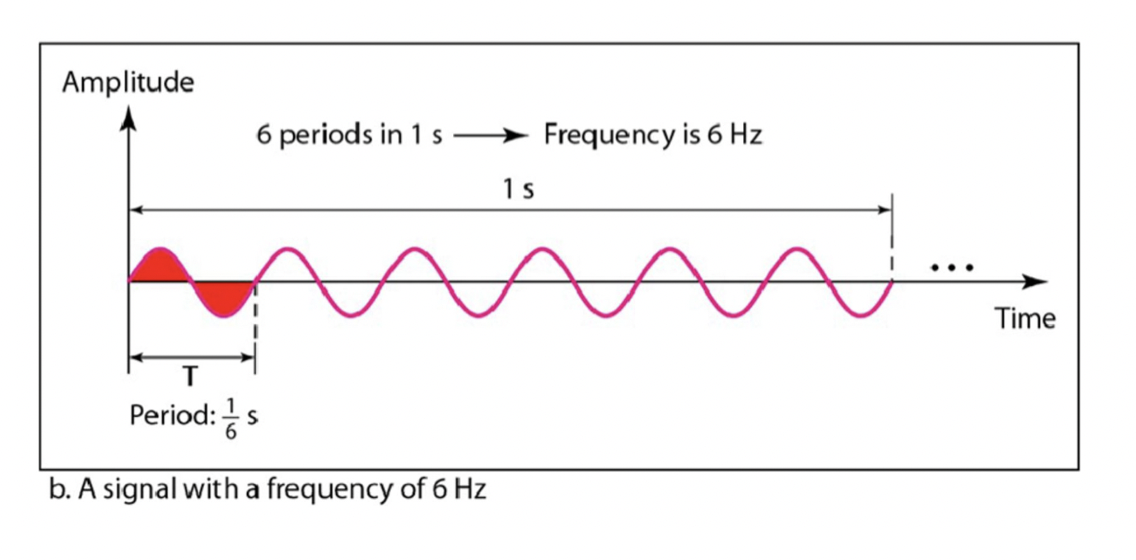
Frequency와 Period의 관계 : 역수 관계

• 주파수는 일정 시간 동안 반복되는 주기 신호의 횟수를 나타내는 값이며, 단위는 헤르츠(Hz)로 표현됩니다.
• 주기는 주기적인 신호에서 한 주기의 길이(시간)를 나타내는 값이며, 단위는 초(s)로 표현됩니다.
• frequency is the reciprocal of period → 주파수와 주기는 역수 관계에 있다는 것입니다. 즉, 주파수는 주기의 역수이며, 주기는 주파수의 역수입니다. 💡 주파수(frequency) = 1 / 주기(period) 주기(period) = 1 / 주파수(frequency) → 예를 들어, 주기가 2초인 주기 신호가 있다면, 해당 신호의 주파수는 0.5Hz입니다. 이는 1초 동안 주기 신호가 0.5번 반복된다는 것을 의미합니다.

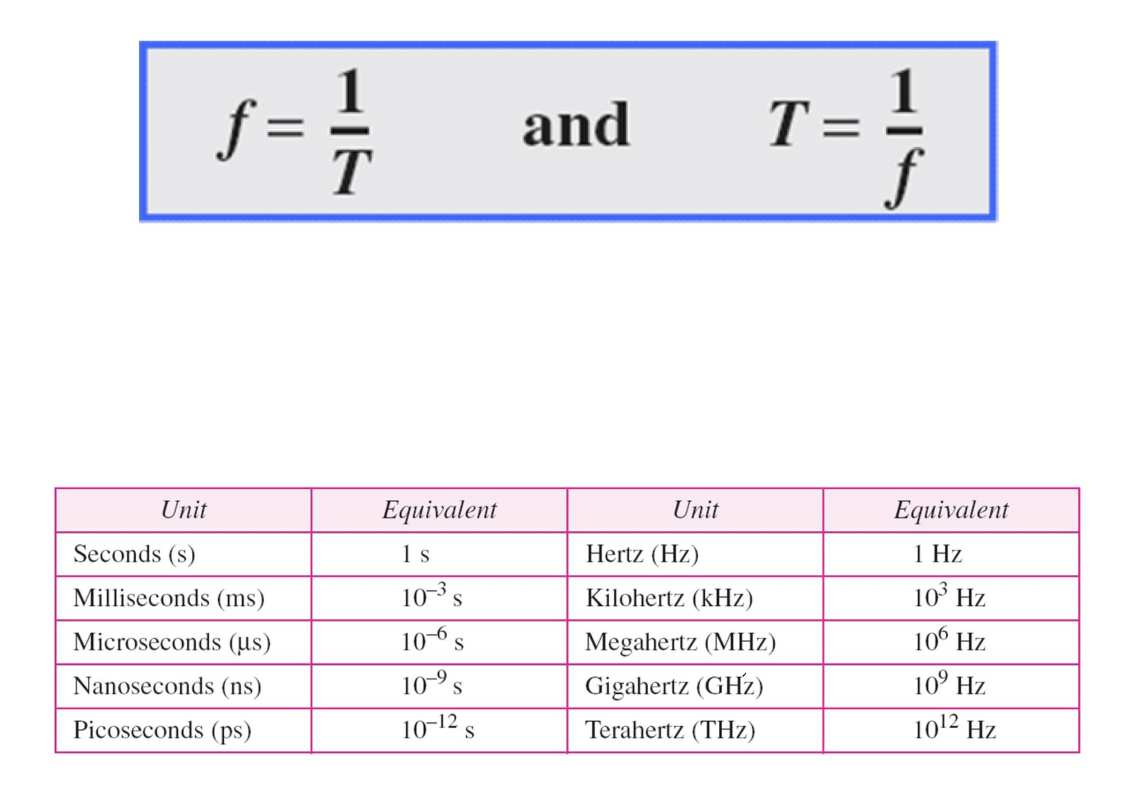
• Frequency indicates how fast a sine wave oscillates. 주파수가 사인파(Sine wave)가 진동하는 속도를 나타낸다. 사인파는 주기적으로 반복되는 파형이며, 한 주기(period) 동안 완전한 한 번의 진동을 한다고 할 수 있습니다. 주파수는 사인파가 일정 시간 동안 몇 번 진동하는지를 나타내는 값으로, 주파수가 높을수록 사인파는 빠르게 진동하게 됩니다. 예를 들어, 1초 동안 사인파가 100번 진동한다면, 해당 사인파의 주파수는 100Hz입니다. 이는 1초 동안 사인파가 100번 진동한다는 것을 의미합니다. 💡 Fast : high frequency 💡 Slow : low frenquency

• A signal that does not change over time – zero frequency – period is infinite 시간에 따라 변화하지 않는 신호는 주파수(frequency)가 0이며 주기(period)가 무한대(infinite) 이러한 신호를 상수(constant) 또는 DC(Direct Current) 신호
  
• A signal that changes instantaneously – infinite frequency – period is zero 순간적으로 값이 바뀌는 신호는 주파수가 무한대(infinite)이며 주기가 0(zero) 이러한 신호를 임펄스(impulse) 또는 디라크 델타(Dirac delta) 함수
  

Phase 위상

• The position of the waveform relative to time 0 시간 0과의 관계에 따른 파형의 위치를 의미합니다. 이는 파형이 시간에 따라 언제 시작되는지 또는 언제 피크값을 가지는지를 나타내는 개념입니다. 예를 들어, 어떤 파형이 1초 후에 시작되고, 그리고 2초 후에 최대값을 가진다면, 이러한 파형의 시간 0과의 상대적 위치는 1초 이전입니다. 따라서 이는 파형이 시간상 언제 시작되는지를 나타내는 것입니다. 이 개념은 파형의 특성과 주파수 분석을 위해 중요합니다. 파형의 시작점과 끝점, 그리고 피크값의 위치에 따라 파형의 형태와 주파수 분석 결과가 달라질 수 있습니다.
  

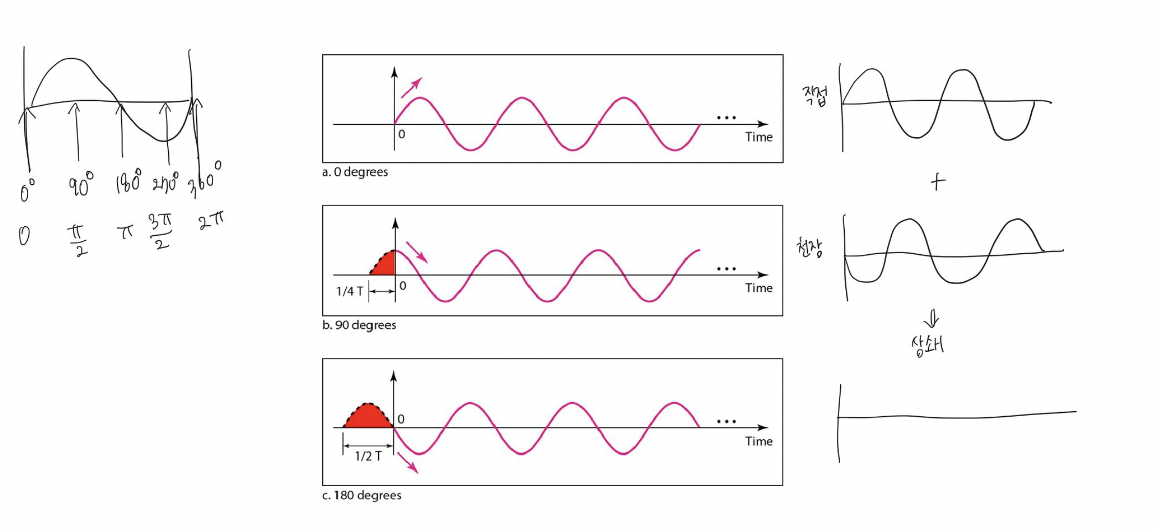
• Phase의 단위 : Degree vs Radain 💡 Degree : 0 - 360도 Radian : 0 - 2 pi ex) 90도 = 1/2 pi 180도 = pi 270도 = 3/2 pi 360도 = 2 pi

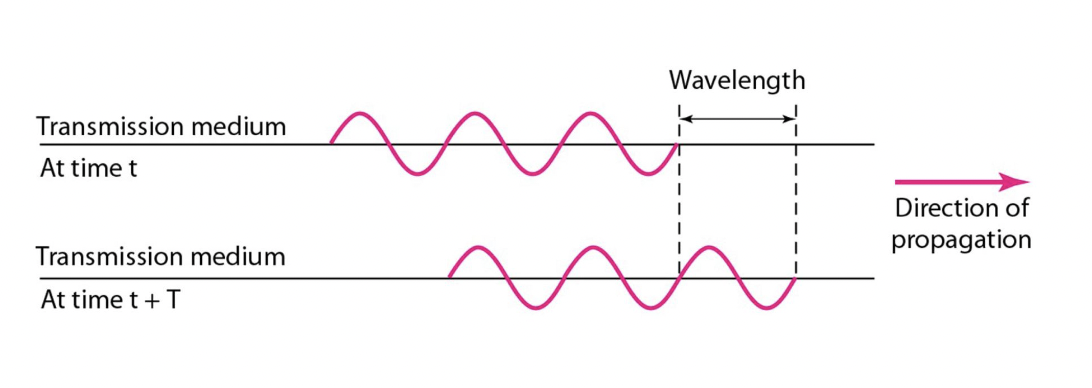
Wavelength (ramda) 파장

length of a period in time 주기의 길이

• wavelength = propagation speed x period = propagation speed / frequency
• 파장 = 전송 속도 x 주기 = 전송 속도 / 주파수
• ramda = c / f

Time domain vs Frequency domain

• Time domain과 frequency domain은 신호를 다른 방식으로 분석하는 두 가지 방법입니다.
• 시간 영역과 주파수 영역은 서로 보완적인 개념으로, 어떤 분야에서는 시간 영역, 어떤 분야에서는 주파수 영역에서의 분석이 더 유용한 경우가 있습니다. 예를 들어, 음성 인식 분야에서는 주파수 영역에서의 분석이 중요하고, 전기 신호 처리 분야에서는 시간 영역에서의 분석이 중요합니다.
• 보통 frequency domain을 더 자주 사용한다!

Time domain

• 시간 영역(Time domain)에서는 신호가 시간에 따라 어떻게 변화하는지를 분석합니다. 이는 일반적으로 시간을 x축으로 하고, 신호값(예: 전압, 소리, 이미지 등)을 y축으로 하는 그래프로 표현됩니다. 이러한 그래프를 시간 도메인 그래프(time domain graph)라고 합니다. 시간 영역에서는 신호의 시작점, 끝점, 진폭, 주기, 주기성 등을 분석할 수 있습니다.
• The X-axis of a graph indicates time. 그래프의 x축이 시간을 나타낸다.
  
• 전기 신호 처리 분야

Frequency domain

• 주파수 영역(Frequency domain)에서는 신호를 주파수 스펙트럼으로 분해하여 분석합니다. 이는 일반적으로 주파수를 x축으로 하고, 해당 주파수에 대한 신호의 성분 값을 y축으로 하는 그래프로 표현됩니다. 이러한 그래프를 주파수 도메인 그래프(frequency domain graph)라고 합니다. 주파수 영역에서는 신호의 주파수 구성 요소, 대역폭, 필터링, 변조, 복조 등을 분석할 수 있습니다.
• The X-axis of a graph indicates frequency. 그래프의 x축이 주파수를 나타낸다.
  
• 음성 인식 분야

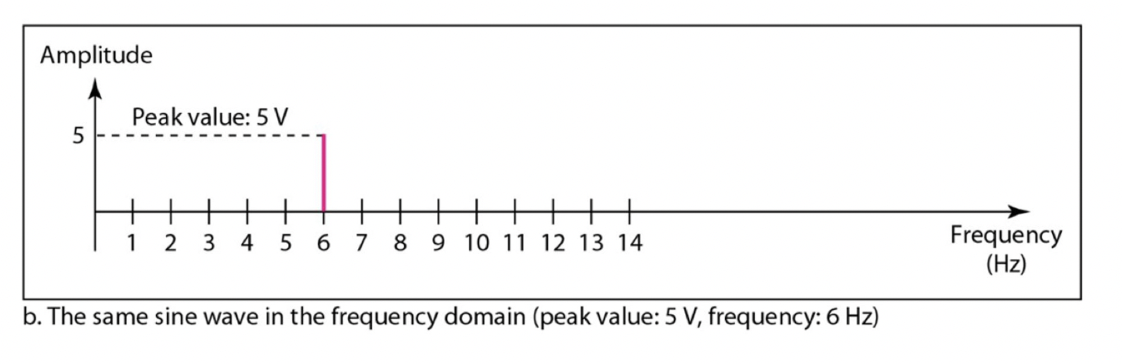
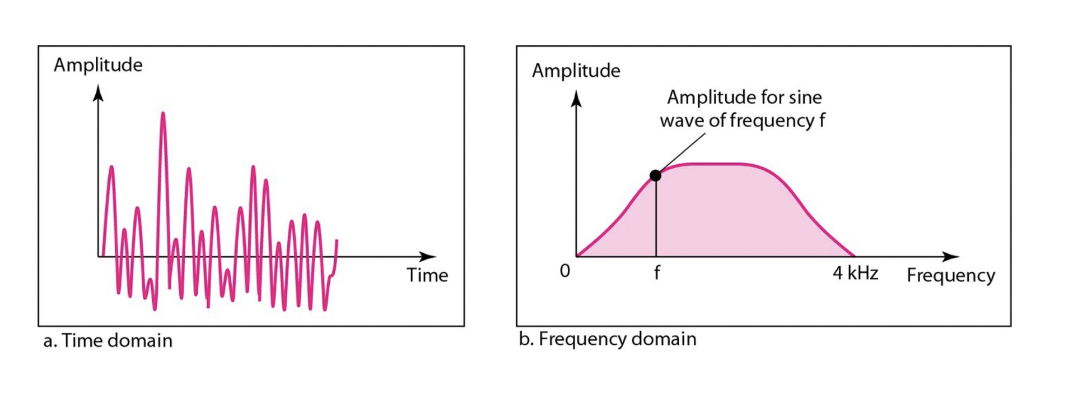
• A simple sine wave becomes a single point in the frequency-domain graph.

주파수 영역에서는 주파수를 x축으로 하는 그래프로 신호를 분해하여 표현합니다. 단일 주파수를 가진 간단한 사인파는 주파수 영역에서는 그래프 상에서 하나의 점으로 표현됩니다. 이는 주파수 도메인에서 해당 신호의 주파수 성분이 하나뿐이기 때문입니다. 즉, 시간 영역에서는 복잡한 모양일지라도, 주파수 도메인에서는 해당 신호의 주파수 성분만 나타나는 것입니다. 따라서, 주파수 영역에서는 해당 신호의 주요 주파수 성분을 쉽게 확인할 수 있습니다.

💡 단일 주파수를 가진 간단한 사인파는 주파수 영역에서는 그래프 상에서 하나의 점으로 표현

• The frequency domain is more compact and useful when dealing with more than one sine wave.

여러 주파수 성분을 가진 복잡한 신호의 경우, 주파수 영역에서 해당 신호를 분석하는 것이 더 효과적입니다. 이는 주파수 도메인에서는 주파수 성분들이 분리되어 표현되기 때문입니다. 복잡한 신호에서 여러 주파수 성분을 분석하기 위해서는 시간 영역에서는 신호를 분해하는 것이 매우 어렵거나 불가능할 수 있지만, 주파수 영역에서는 여러 주파수 성분들을 쉽게 분리하여 분석할 수 있습니다.

또한, 주파수 영역에서는 복잡한 신호에서의 주요 주파수 성분이 빠르게 확인됩니다. 예를 들어, 음악 신호에서 특정 주파수가 음악의 리듬이나 화음을 결정하는 역할을 할 수 있습니다. 이러한 특징들은 주파수 도메인에서 더욱 뚜렷하게 확인할 수 있습니다.

따라서, 여러 주파수 성분을 가진 복잡한 신호의 분석에서는 주파수 영역에서의 분석이 더욱 효과적이며, 더욱 간결하고 유용한 정보를 제공할 수 있습니다.

💡 복잡한 신호 분석은 frequency domain이 더욱 효과적!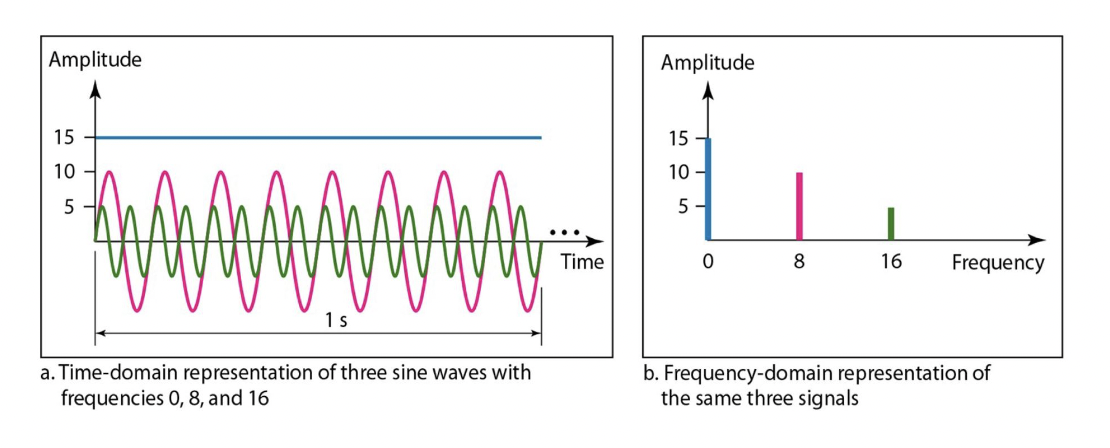

→ time domain 은 여러 주파수가 몰렸을 때 매우매우 복잡

→ frequency domain은 주파수 성분들이 분리되어 표현되므로 매우매우 간결함!

Compositie Signal 복합 신호

1. Periodic Composite Signal → discrete frequencies

   복합 신호가 주기성 신호인 경우, 이는 이산 주파수(분리주파수)를 가진 여러 신호로 구성된 것으로 주파수 영역에서 나타납니다. 이러한 이산 주파수 성분은 주기성 신호의 주파수 및 진폭과 관련되어 있습니다. 이산 주파수 성분을 분석함으로써, 우리는 주기성 신호의 주요 특성을 파악할 수 있습니다.

2. Aperiodic Composite Signal → continuous frequencies

   복합 신호가 주기성이 아닌 경우, 이는 연속적인 주파수를 가진 여러 신호로 구성된 것으로 주파수 영역에서 나타납니다. 이러한 연속적인 주파수 성분은 주기성이 없는 신호의 주파수 및 진폭과 관련되어 있습니다. 연속적인 주파수 성분을 분석하기 위해서는, 우리는 주파수 영역에서 적분을 수행하여 주요 특성을 파악합니다.

→ 따라서, 주기성이 있는 신호와 주기성이 없는 신호는 주파수 영역에서 서로 다른 방식으로 나타나며, 주파수 성분의 종류와 수량도 다르게 나타납니다.

Composite Periodic Signal 복합 주기 신호

• 복합 주기 신호는 단일한 사인파와 같지 않으며(not a simple sine wave), 여러 주파수, 진폭 및 위상의 단순한 사인파로 구성된 신호입니다. 즉, 여러 개의 주파수 성분으로 이루어진 신호입니다.
• 하지만 이러한 복합 주기 신호는 각각의 주파수 성분으로 분해될 수 있습니다. 이를 푸리에 변환(Fourier transform)이라고 합니다. 푸리에 변환을 통해 복합 주기 신호를 각각의 주파수 성분으로 분해하면, 단일한 사인파들로 구성된 주파수 영역의 그래프를 얻을 수 있습니다.
• 이러한 방식으로 복합 주기 신호를 각각의 주파수 성분으로 분해하면, 각 주파수 성분의 진폭, 주파수 및 위상을 분리하여 분석할 수 있습니다. 따라서, 푸리에 변환은 실제 세계에서 발생하는 다양한 복잡한 신호를 분석하는 데 중요한 도구가 됩니다.

💡 복합 주기 신호는 하나의 simple 사인파가 아니라 여러 simple 사인파들로 구성된 신호. 💡 하지만, 푸리에 변환을 통해 복합 주기 신호를 각각의 주파수 성분으로 분해하면 simple 사인파들로 구성된 주파수 영역의 그래프를 얻을 수 있음

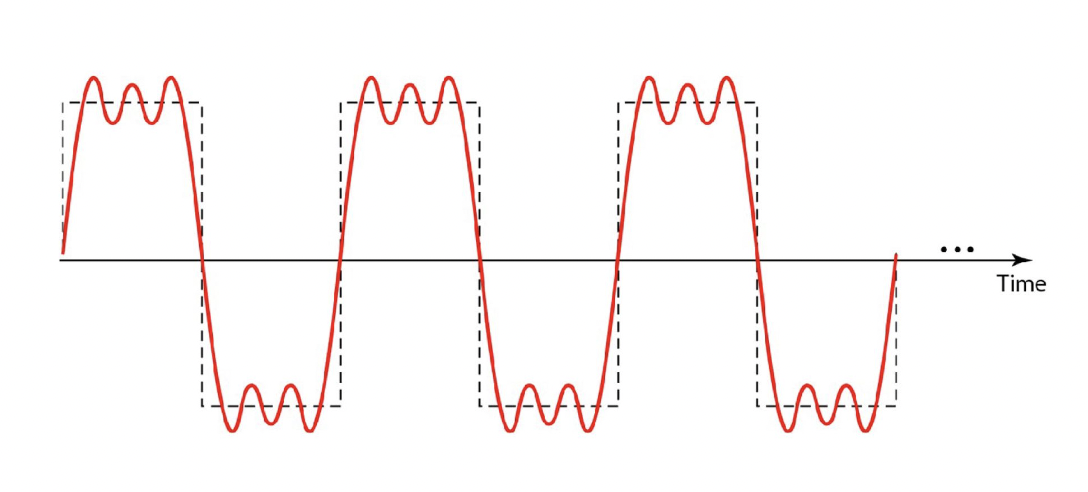
• Time-domain decomposition 타임 도메인의 분해

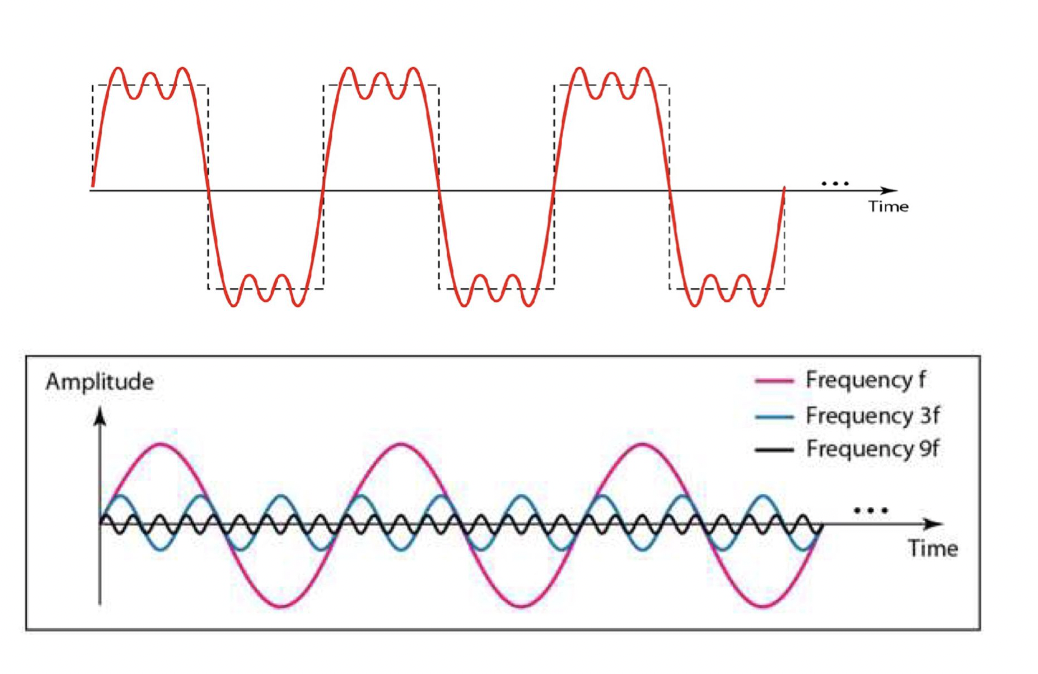
→ 3개의 Frequency f, 3f, 9f 그래프를 합치면 위의 그래프처럼 보임!

• Frequency-domain decomposition 주파수 도메인의 분해

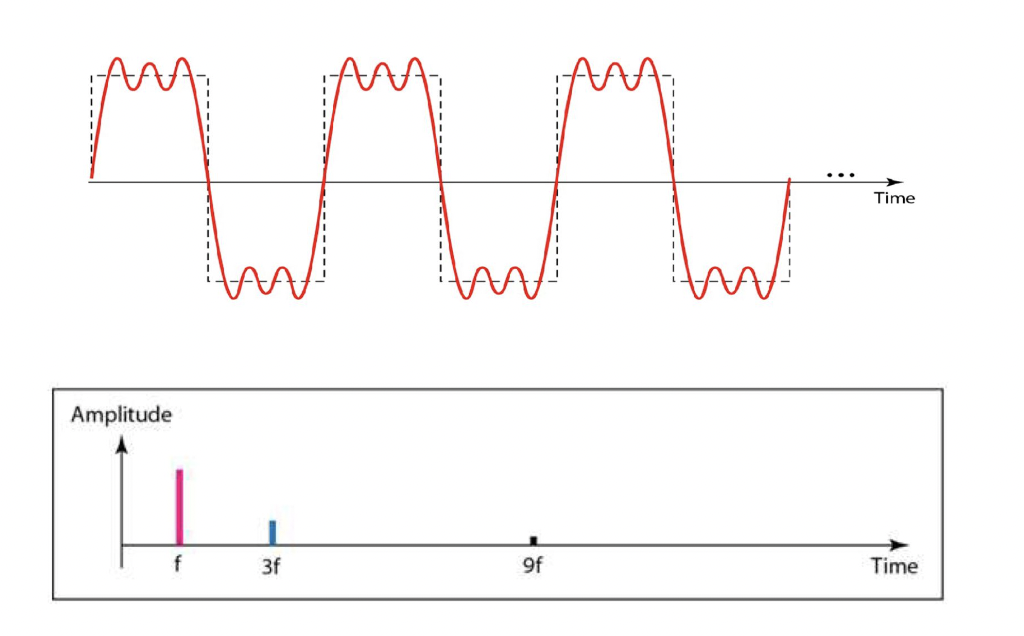
→ 3개의 Frequency f, 3f, 9f 그래프를 합치면 위의 그래프처럼 보임!

Aperiodic composite signal 주기성이 없는 복합 신호

• 일정한 주기성을 가지지 않고, 불규칙하게 변하는 신호
• 예를 들면 음성 신호나 노이즈 신호
• 단순 사인파로 분해될 수 없습니다. 대신, 이러한 신호를 분석하려면 다양한 분석 기술이 필요합니다. 이 중 하나는 푸리에 변환을 사용하여 주파수 영역에서 신호를 분석하는 것입니다. 그러나 aperiodic composite signal의 분석은 주기성 신호에 비해 더 복잡하며, 시간 및 주파수 영역에서 다양한 특성을 가지고 있기 때문에 처리가 어려울 수 있습니다.

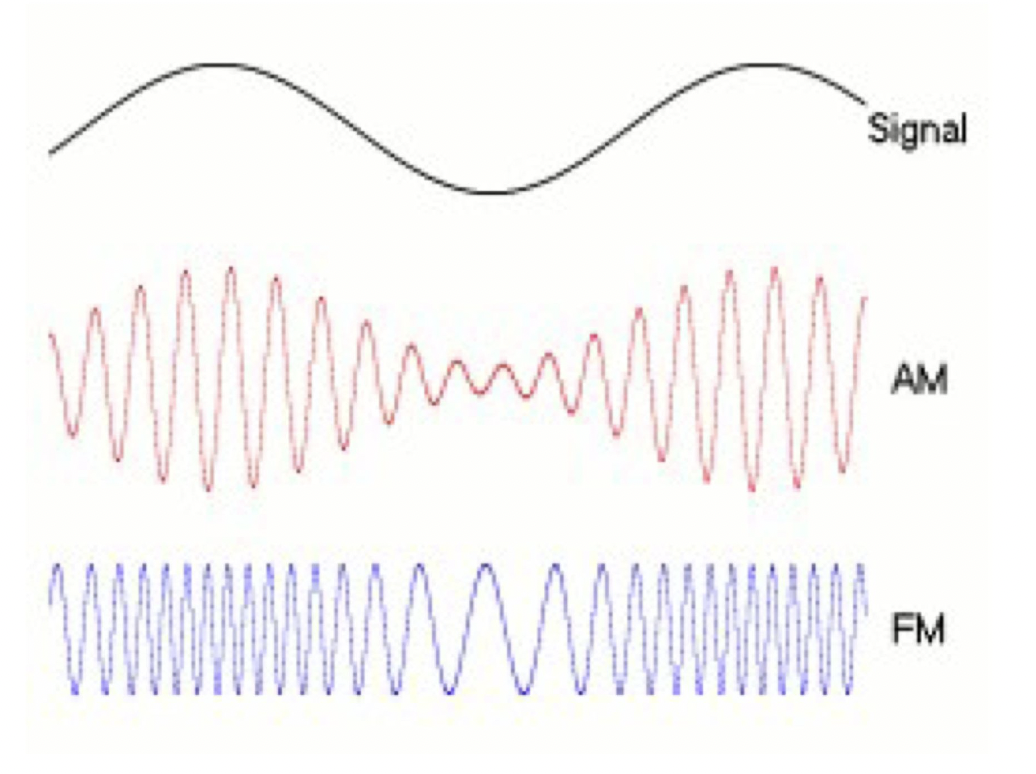
AM & FM

AM과 FM은 모두 무선 통신에서 사용되는 변조 기술입니다.

AM radio(Amplitude Modulation) : 진폭 변조

AM은 진폭 변조(Amplitude Modulation)의 약어로, 캐리어파의 진폭을 변조하여 정보를 전송하는 방식입니다. 즉, 원래의 캐리어파에 음성이나 데이터 등의 정보를 올려놓고, 이 정보가 적용된 새로운 전파를 송신하는 방식입니다. AM 방식은 전파의 진폭이 변화하므로 전파의 세기에 대한 변화가 민감하게 작용합니다. AM 방식은 오래 전부터 사용되어 왔으며, 주로 AM 라디오 방송에서 사용됩니다.

→ 진폭을 이용

→ Each channel has 10kHz bandwith

→ 530-1700kHz band

FM radio(Frequency Modulation) : 주파수 변조

FM은 주파수 변조(Frequency Modulation)의 약어로, 캐리어파의 주파수를 변조하여 정보를 전송하는 방식입니다. AM과 달리 전파의 진폭은 일정하고 주파수만 변화합니다. FM 방식은 전파의 주파수가 변화하므로 전파의 진폭에 대한 변화는 크게 작용하지 않습니다. FM 방식은 주로 FM 라디오 방송, 텔레비전 등에서 사용됩니다. FM 방식은 AM 방식에 비해 노이즈에 강합니다.

→ 주파수를 이용

→ Each channel has 200kHz bandwith

→ 88-108MHz band

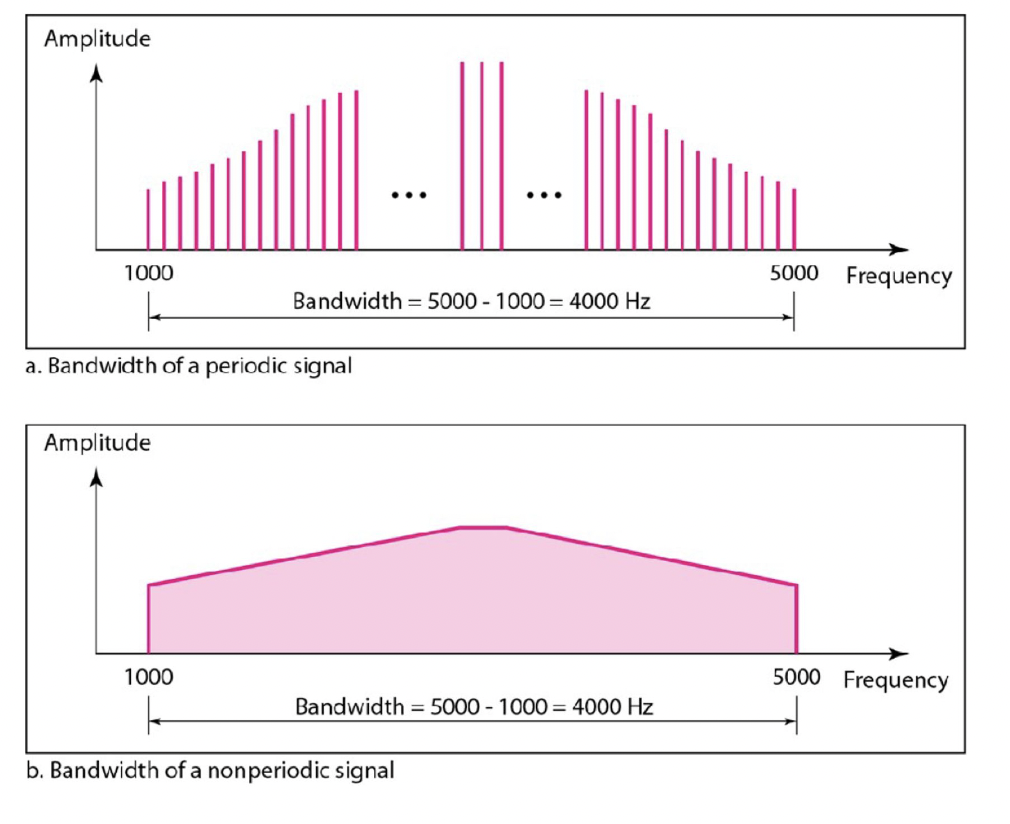
Bandwith = 가장 높은 주파수 - 가장 낮은 주파수

• the range of frequencies contained in a composite signal. 복합 신호 내에 포함된 주파수 범위를 의미합니다.
  
• 가장 높은 주파수(the highest frequency)와 가장 낮은 주파수(the loweset frequency) 간의 차이를 계산하여 구합니다.
• 일반적으로는 신호가 얼마나 많은 주파수를 포함하고 있는지를 나타내는 척도로 사용됩니다. 대역폭이 넓을수록 신호는 더 많은 주파수를 포함하고 있으며, 좁을수록 더 적은 주파수를 포함하고 있습니다. 대역폭은 주파수 분석, 통신, 신호 처리 등 다양한 분야에서 중요한 개념으로 사용됩니다.

Digital Signal

Signals that contain bit information (0, 1) using amplitude, frequency and phase.

디지털 신호는 0과 1의 비트 정보를 전송하기 위해 아날로그 신호에서는 진폭, 주파수 및 위상과 같은 특성들을 이용하여 변조됩니다. 디지털 신호는 이진 코드 (binary code)를 사용하여 0과 1을 표현하며, 각각의 비트는 특정한 주기와 진폭을 가지는 일련의 디지털 신호로 변환됩니다. 이러한 디지털 신호는 전송 중에 노이즈와 왜곡에 영향을 받지 않기 때문에, 통신 시스템에서 매우 중요한 역할을 합니다.

ex) bit 1 → 5V , bit 0 → 0V

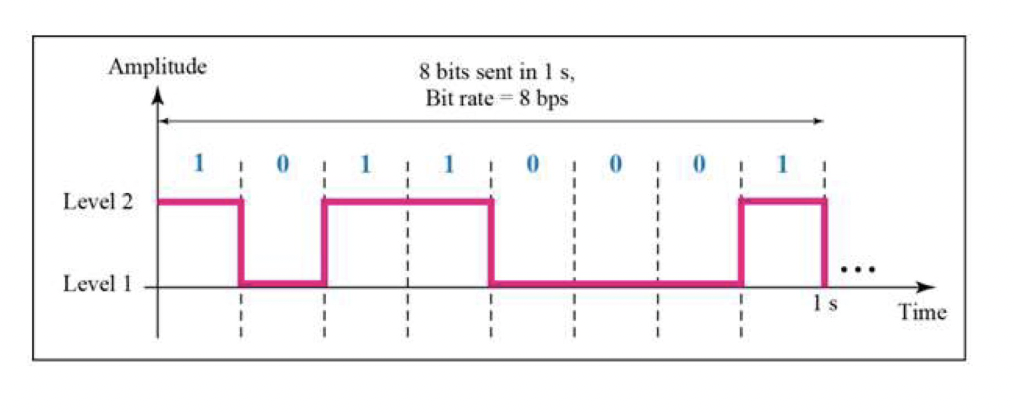
신호의 레벨은 2개 이상일 수 있습니다. 예를 들어, 4개의 레벨이 있으면 두 개의 비트 정보를 담을 수 있습니다. 예를 들어, 레벨 1은 00, 레벨 2는 01, 레벨 3은 10, 레벨 4는 11과 같이 각 레벨에는 2개의 비트 정보가 포함됩니다.

: 4개의 level → 2개의 bit 정보(2^2=4)

: 8개의 level → 3개의 bit 정보(2^3=8)

💡 2^n개의 level → n개의 bit 정보

ex)

• Level 1: 00
• Level 2: 01
• Level 3: 10
• Level 4: 11

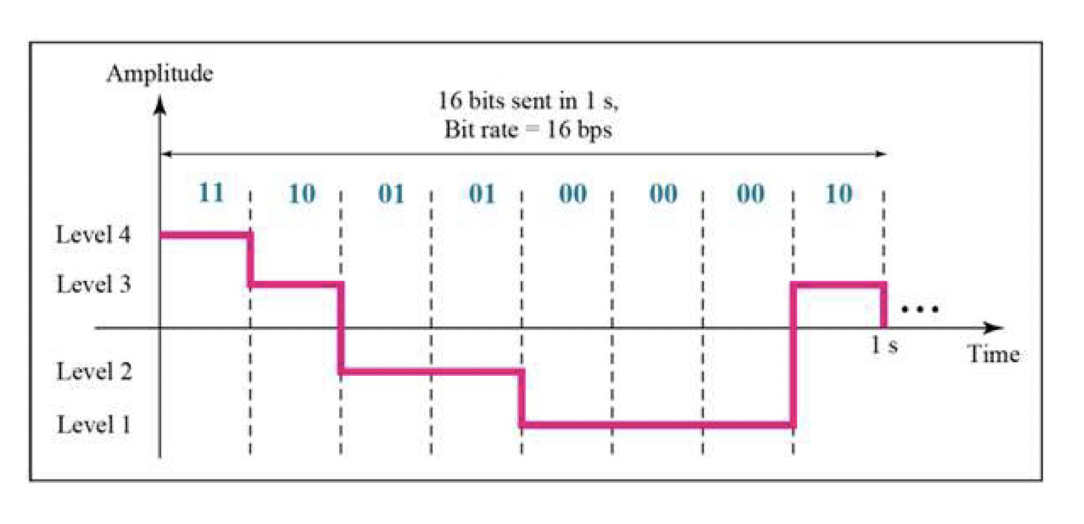
Transfer rate(bit rate) (단위 : bps(bits per second))

💡 bps = bits/second

데이터 전송 속도

• 1 Kbps = 1000 bps
• 1 Mbps = 1000 Kbps
• 1 Gbps = 1000 Mbps

Digital Signals

A digital signal is a composite analog signal with infinite bandwidth.

디지털 신호는 무한 대역폭을 가진 복합 아날로그 신호입니다.

디지털 신호는 이산적인 값으로 이루어져 있으며, 이산 시간에서 정의됩니다. 이산 시간에서는 시간이 연속적인 값이 아니라 순서대로 측정된 샘플링 값으로 나눠집니다. 따라서, 디지털 신호는 이산적인 레벨을 가지고 있으며 무한대의 대역폭이 필요하지 않습니다.

반면, 아날로그 신호는 연속적인 값을 가지며 무한대의 대역폭이 필요합니다. 따라서, 디지털 신호는 아날로그 신호와는 다른 종류의 신호이며, "디지털 신호는 무한대의 대역폭을 가지는 아날로그 신호의 복합체"라는 설명은 부적절합니다.

Time domain of a digital signal

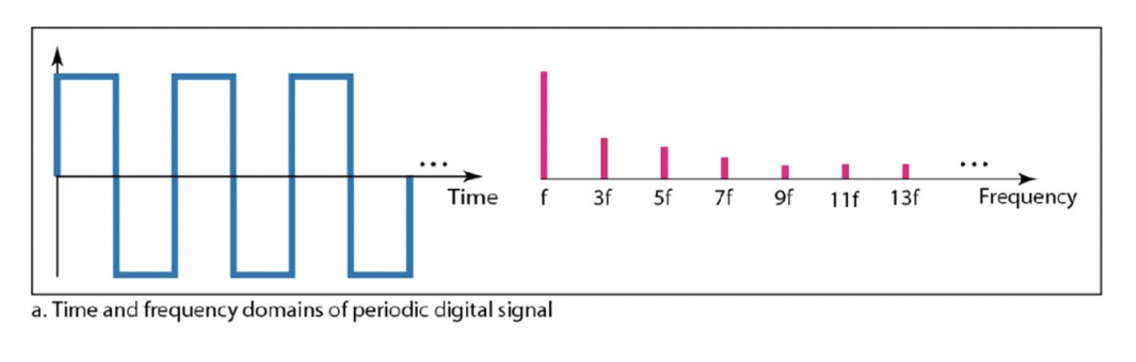
Frequency domain of a digital signal

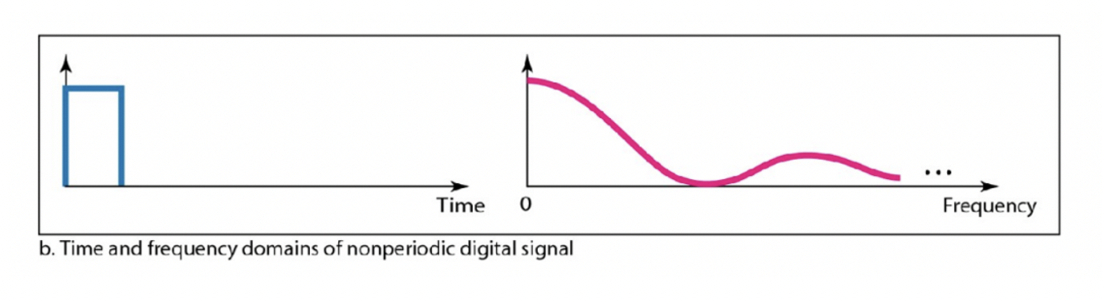
Baseband Transmission

Baseband Transmission은 디지털 신호를 전송하기 위한 가장 간단한 방법 중 하나입니다. 이 방법은 디지털 신호를 "그대로" 전송하는 것으로, 디지털 신호를 아날로그 신호로 변환하지 않고, 주파수 영역에서 아주 낮은 주파수 대역을 사용하여 디지털 신호를 전송합니다. 이 방식은 무선 통신에서는 AM 방식으로, 유선 통신에서는 직접 전기 신호로 변환하여 전송합니다. 그러나 이 방법은 무선 통신에서는 제한된 전송 거리와 대역폭을 가지고 있으며, 유선 통신에서는 직접 전기 신호로 변환하여 전송하기 때문에 전송 시스템에서 아날로그-디지털 변환 회로가 필요합니다.

The simplest way to transmit a digital signal is to transmit "as it is".

전송하려는 디지털 신호를 그대로 전송하는 가장 간단한 방법은 baseband 전송이다. 즉, 디지털 신호의 모든 정보를 전송하고자 하는 채널에 직접 주는 것이다. 이 방식은 매우 (+)단순하고 직접적이지만, (-)전송 거리가 짧아야 하며, 신호에 노이즈가 있는 경우에는 신호 품질이 크게 저하될 수 있다. 이 방식은 보통 LAN (Local Area Network)이나 짧은 거리 통신에 사용된다.

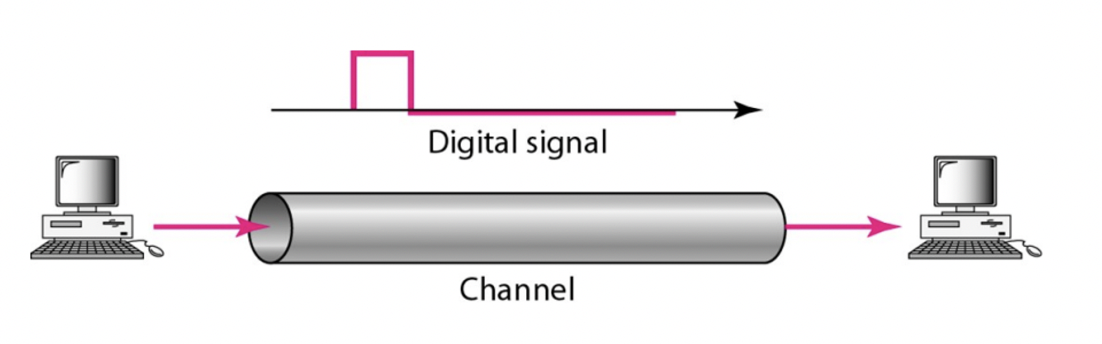
디지털 신호를 "그대로" 전송하기 위해서는 무한한 대역폭을 갖춘 채널이 필요합니다. 이를 베이스밴드 전송이라고 합니다. 이를 가능하게 하려면 영 주파수부터 신호를 통과시킬 수 있는 저역통과 채널(Low-pass channel)이 필요합니다.

• Low-pass channel: channel that can pass signals from zero frequency 제로 주파수(0Hz)를 포함한 낮은 주파수 신호를 전달할 수 있는 채널을 말합니다. 따라서 이 채널에서는 주파수가 낮은 신호는 잘 전달되지만, 고주파수 신호는 감쇠되거나 차단됩니다. 이러한 특성 때문에, 이 채널을 통해 전달되는 디지털 신호는 아날로그 신호와 달리, 주파수 영역에서 신호가 일정하지 않으며, 정보가 손실될 수 있습니다.
  

Real-life media cannot have infinite bandwidth. Some frequency components are cut from the original signal, leaving an approximate signal.

현실적인 미디어는 무한한 대역폭을 가질 수 없습니다. 따라서 원래 신호에서 일부 주파수 성분이 잘리고 근사 신호만 남게됩니다.

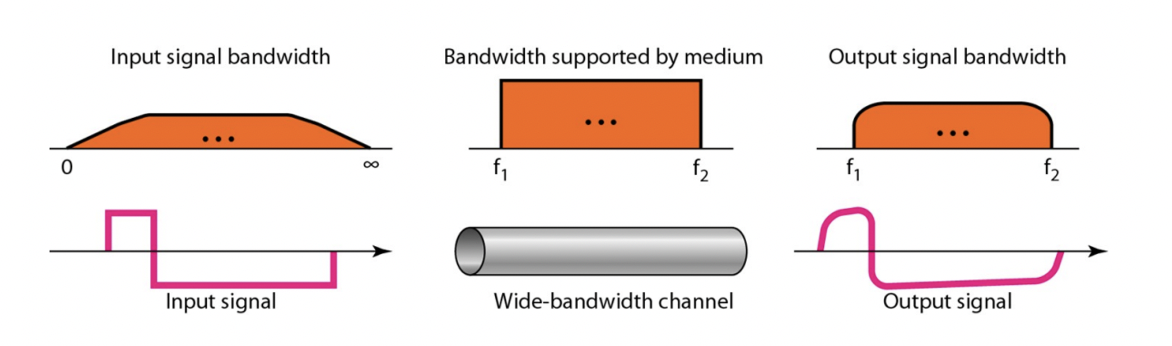
The more bandwidth we use, we get an approximate signal that is closer to the original.

사용하는 대역폭이 더 넓을수록 원래 신호에 더 가까운 근사 신호를 얻게 됩니다.

💡 Baseband Transmission은 **디지털 신호를 변조하지 않고 직접 전송**하는 방법입니다. 이 방법을 사용하면 **원래 디지털 신호와 거의 동일한 신호를 전송**할 수 있습니다. 그러나 **실제로는 사용 가능한 대역폭이 제한**되기 때문에 **전송되는 신호는 원래 신호의 근사치**일 수밖에 없습니다.

이때 사용 가능한 대역폭이 더 넓을수록, 전송되는 신호는 원래 신호에 더 가까워집니다. 왜냐하면 더 넓은 대역폭을 사용하면 더 많은 주파수 성분을 전송할 수 있기 때문입니다. 즉, 전송되는 신호는 원래 신호에 더 많은 주파수 성분을 포함하므로 원래 신호에 더 가까워집니다.

• bandwidth가 많을수록 더 나은 근사치를 만들 수 있다!

→ 만들 수 있는 그래프의 모양이 더 다양하기 때문!

• bandwidth needed for baseband transmission is proportional to transfer rate. baseband transmission에서 필요한 대역폭이 전송 속도에 비례한다. 더 많은 대역폭은 더 나은 근사치를 제공하여 더 높은 정확도를 얻을 수 있습니다. 즉, 대역폭이 더 넓을수록, 신호가 더 많은 원래의 정보를 포함하게 되므로, 전송 속도가 높아질수록 더 많은 대역폭이 필요하게 됩니다.
  

## Summary : Baseband Transmission

- Baseband transmission은 디지털 신호를 원래의 형태 그대로 전송하는 방법입니다.
- 왜곡되지 않은 디지털 신호를 전송하기 위해서는 무한대의 대역폭이 필요합니다. 그러나 무한대의 대역폭은 불가능하기 때문에 근사한 신호를 전송하게 됩니다.
- 전송 속도는 대역폭에 비례합니다.
- **N bps**로 데이터를 전송하려면, 최소한 **N/2의 대역폭**이 필요합니다. 대역폭 f가 주어졌을 때, 최대 전송 속도는 2f입니다.
    
    <aside>
    💡 N/2 Hz의 대역폭 bandwidth (N : 전송속도 transfer rate, bit rate)
    bandwidth = N/2
    
    </aside>
    

- Baseband transmission is a way to transmit a digital signal in its original form
- To transmit undistorted digital signal, we need infinite bandwidth (which is impossible)
- Transfer rate is proportional to bandwidth
- To send data at N bps, we need at least N/2 bandwidth
    
    – If we have a bandwidth f, maximum transfer rate is 2f
    

Band-pass channel

특정 주파수 대역의 신호만 전달할 수 있는 채널을 말합니다. 이러한 채널은 고주파와 저주파를 필터링하여 일정 주파수 범위 내(f1부터 f2까지의 주파수 범위 내)에서만 신호를 전달합니다. 이는 실제 세계에서 발생하는 대부분의 채널에서 관찰되는 현상입니다. 따라서 이러한 채널을 사용하여 디지털 신호를 전송할 때는, 전송하려는 디지털 신호가 해당 주파수 범위 내에 포함되도록 신호를 조작해야 합니다. 이를 위해 디지털 변조 기술이 사용됩니다. 이를테면, 라디오 방송에서 특정 주파수 대역에서만 음악이나 대화를 들을 수 있는 것이 바로 Band-pass channel의 예시입니다.

• Passes frequencies from f1 to f2 (f1 > 0) → 특정 주파수 내
• A realistic channel

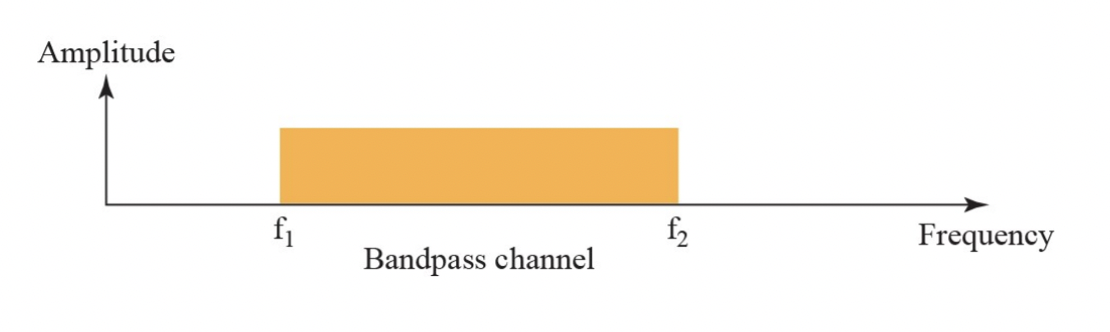
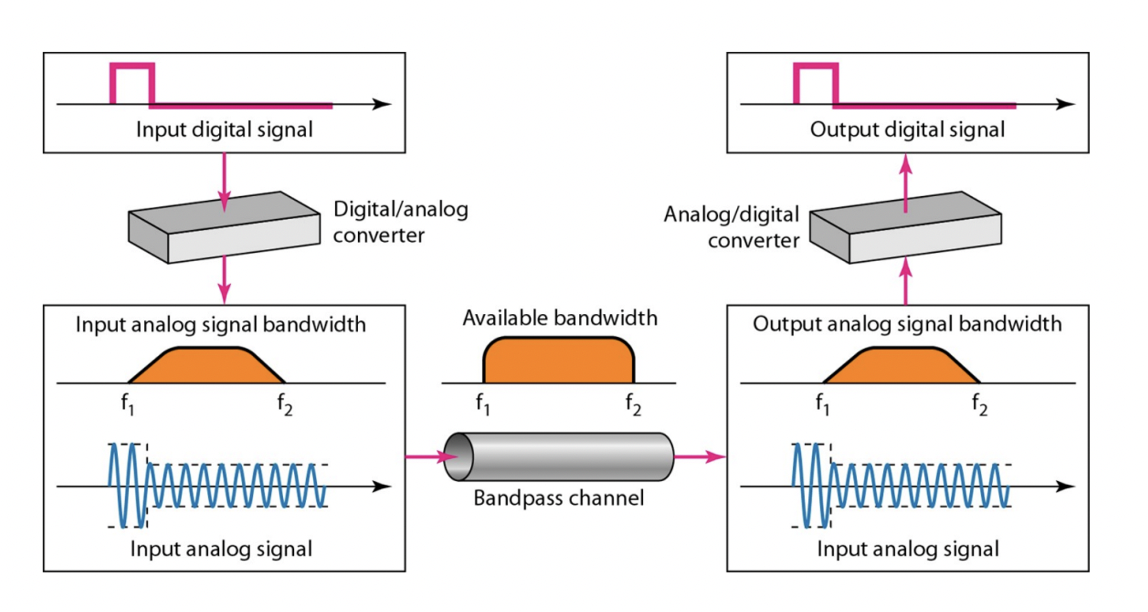
Band-pass channel Modulation

• Band-pass channel에서 디지털 신호를 전송하려면, 디지털 신호를 아날로그 신호로 변조해야 합니다. 이 과정을 "모듈레이션(Modulation)"이라고 합니다.
• 모듈레이션은 주파수, 위상 또는 진폭 등을 변경하여 아날로그 신호를 만들어냅니다.
• 변조된 신호를 전송 후, 수신 측에서는 다시 디모듈레이션(Demodulation) 과정을 거쳐 원래의 디지털 신호로 변환합니다. 이 방식은 라디오, 텔레비전 등에서 널리 사용되는 방법입니다.

Baseband vs Broadband

• Baseband와 broadband는 데이터를 전송하는 방법 중 두 가지입니다.
• Baseband는 디지털 신호를 그대로 전송하는 방법입니다. 따라서, 신호가 저주파에서 전송되며, 전송 대역폭이 적은 것이 특징입니다. → baseband transmission
• Broadband는 아날로그 신호를 변조하여 전송하는 방법입니다. 변조(Modulation)란, 기본적으로 아날로그 신호를 디지털 신호로 바꾸는 과정으로, 이 과정에서 신호는 고주파 신호로 변환됩니다. 따라서, 전송 대역폭이 넓은 것이 특징입니다. → bandpass transmission
• 두 방법의 가장 큰 차이점은 전송 대역폭의 차이입니다. Baseband는 저대역폭을 사용하므로 전송 속도가 느리지만, 신호의 왜곡이 적고 오류가 적습니다. 반면, Broadband는 고대역폭을 사용하므로 전송 속도가 빠르지만, 신호의 왜곡과 오류가 많을 수 있습니다.

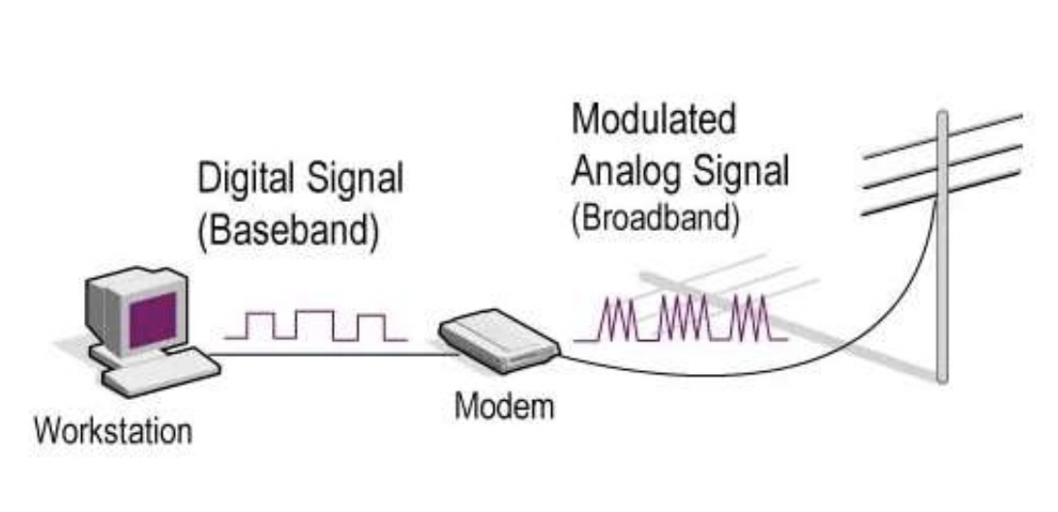
Transmission Impairment

불완전한 미디어는 신호 장애를 유발합니다. 미디어의 시작점에서의 신호는 미디어의 끝에서의 신호와 동일하지 않습니다. (beginning signal =x end signal)

왜? 이 세가지의 원인들 때문에!

• Attenuation 신호감쇄
• Distortion 왜곡
• Noise 노이즈

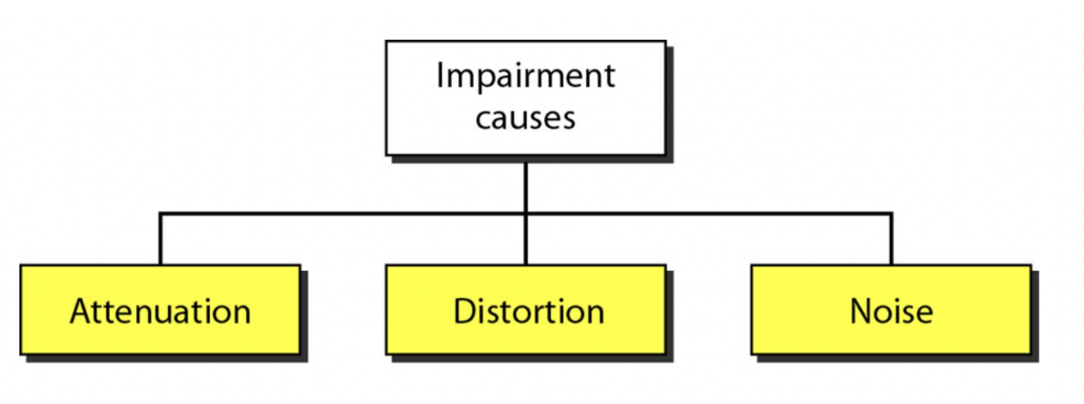
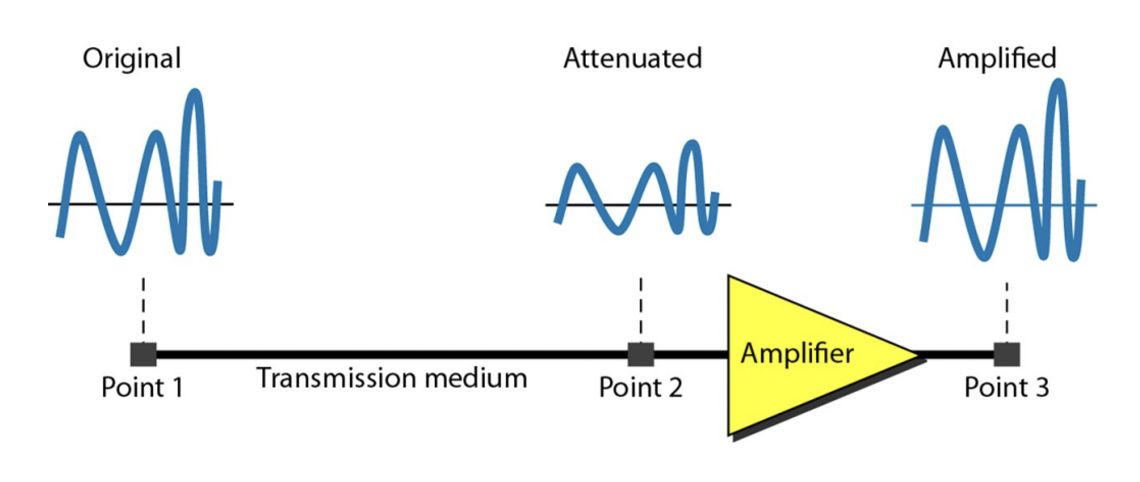
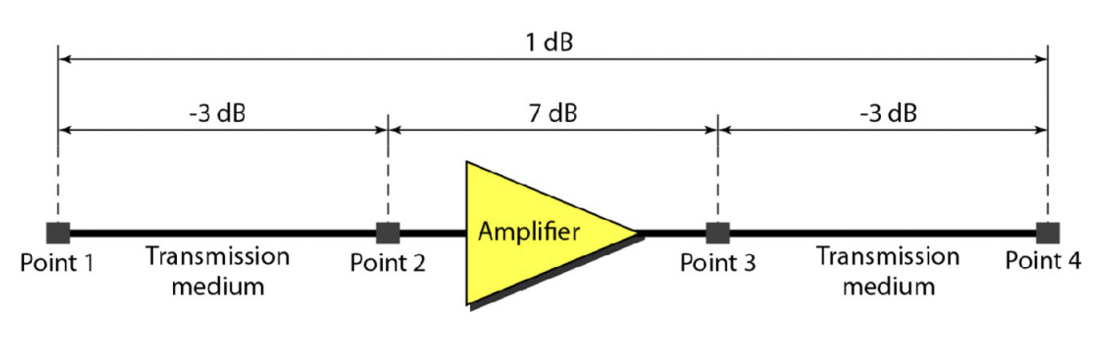
1. Attenuation 신호 감쇄

신호는 매체를 통과하는 동안 에너지를 상실합니다(신호감쇄)

이 때, 신호는 증폭기(Amplifier)를 사용하여 증폭될 수 있습니다. 근데, 증폭기에서 신호 뿐만 아니라 노이즈도 증폭이 되므로 문제가 됩니다.

Signal Strength의 단위

decibel(dB) : 비율

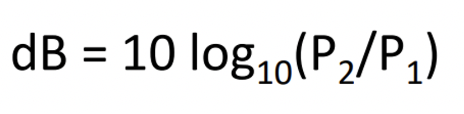
→ dB = 두 signal(p1, p2) strength의 비율(ratio)

→ 데시벨은 신호 세기의 비율!

→ p1 : 전송할 때 세기, p2 : 도착했을 때 세기

→ reduced to one half : p2 = 0.5p1

→ increased 10 times : p2 = 10p1

• 신호 세기의 변화를 측정하기 위해 엔지니어가 데시벨을 사용하는 이유 중 하나는 데시벨 수치가 두 개가 아닌 여러 지점을 측정할 때도 덧셈(또는 뺄셈)이 가능하기 때문입니다.

dBm = dBmW : 절댓값

dBm은 신호의 파워를 밀리와트(mW) 단위로 측정하는 데에 사용됩니다. dBm은 신호의 파워가 1mW일 때의 레벨을 0dBm으로 정의하고, 이보다 높은 파워는 양수 dBm 값으로, 이보다 낮은 파워는 음수 dBm 값으로 나타내집니다. 예를 들어, 신호의 파워가 10mW인 경우, 이를 dBm으로 나타내면 10*log10(10mW/1mW) = 10dBm이 됩니다.

(Pm : power in milliwatt unit)

ex) 1mW = 0dBm = 10log10 1 = 10 x 0 = 0

10mW = 10dBm = 10log10 10 = 10 x 1 = 10

100mW = 20dBm = 10log10 100 = 10 x 2 = 20

1000mW = 30dBm = 10log10 1000 = 10 x 3 = 30

200mW = 23dBm = 10log10 200 = 10 x (2 + 0.3) = 23 (log2 = 0.3)

40000mW = 46dBm = 10log10 40000 = 10 x (4 + 0.6) = 46 (log4 = 0.6)

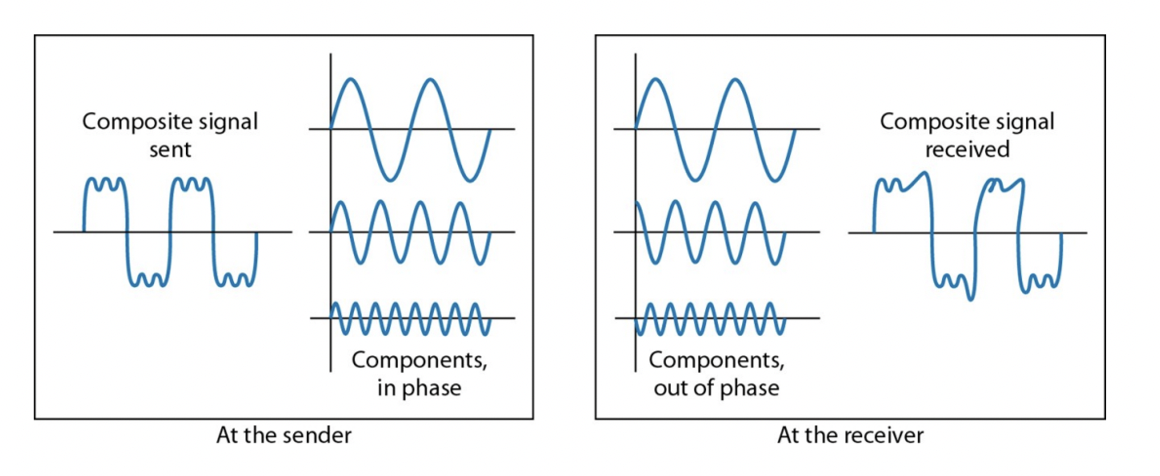
Distortion

신호가 전송되거나 처리되는 동안 신호의 모양이나 형태가 변화한다는 의미입니다. 이것은 신호의 진폭, 주파수, 위상 또는 다른 특성에 대한 변화로 인해 발생할 수 있습니다. 이러한 변화는 신호가 전송되는 경로에서 발생할 수도 있으며, 이는 신호가 전송되는 동안 잡음, 감쇠 또는 왜곡의 형태로 나타날 수 있습니다. 이러한 신호의 변형은 정보를 전달하는 데 문제가 될 수 있으며, 이를 해결하기 위해 다양한 신호 처리 기술이 개발되어 왔습니다.

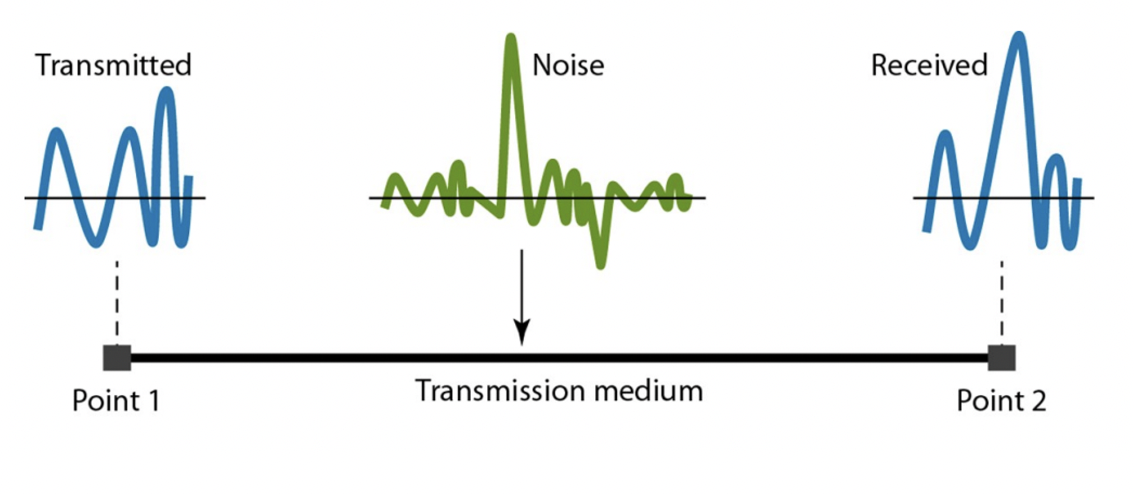
Noise

신호를 망가뜨리는 여러 가지 종류의 잡음이 있습니다. 이 중에는 thermal noise, induced noise, crosswalk, impulse noise 등이 있습니다. 이러한 잡음들은 신호를 손상시킬 수 있습니다.

Signal-to-Noise Ratio(SNR) (단위 : W, dB)

전송되는 신호(Signal)와 함께 전송되는 잡음(Noise)의 비율을 의미합니다. 이는 전송되는 신호의 품질을 나타내는 중요한 척도 중 하나이며, 일반적으로 dB 단위로 표시됩니다. SNR 값이 높을수록 신호의 품질이 더욱 좋아지며, SNR 값이 낮을수록 잡음이 많아져 신호가 왜곡될 가능성이 높아집니다. 따라서 통신 시스템 설계나 평가 시에는 신호 대 잡음비를 고려하여 최적의 전송 조건을 설정하거나, 실제로 전송된 신호를 분석하게 됩니다.

💡 SNR = signal power / noise power 💡 SNR dB = 10log10 (signal power / noise power)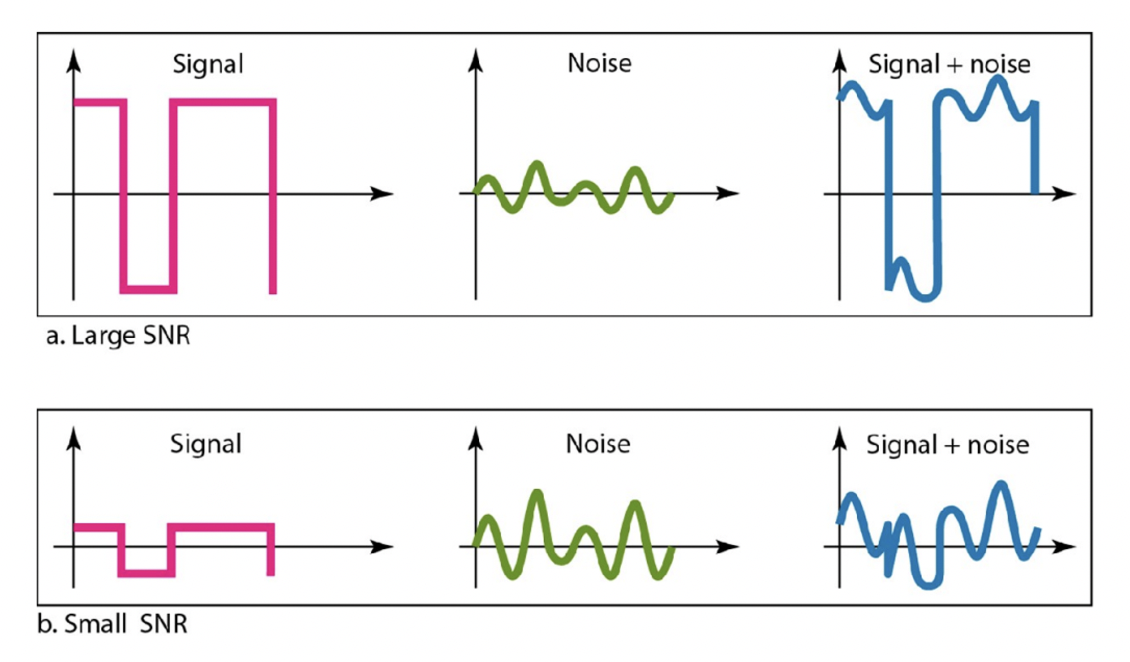

→ signal와 noise의 차이가 크면 SNR이 큼

→ signal와 nosie의 차이가 작으면 SNR이 작음

→ SNR이 너무 작으면(signal와 noise의 차이가 작으면), signal은 회복되지 않음. 여전히 계속 문제 있을 것.

Data Transfer Rate(Bit Rate)

• 데이터 전송률은 세 가지에 의존한다.
  1. Bandwidth
  2. Number of signal levels
  3. Channel quality(noise level)

Nyquist Equation

주어진 대역폭에서 전송할 수 있는 최대 데이터 전송 속도를 계산하는 데 사용되는 방정식입니다. 이 방정식은 대역폭이 2B인 채널에서 전송할 수 있는 최대 데이터 전송 속도를 2 x B x log2 L로 계산합니다. 여기서 B는 bandwidth, L은 전송에 사용되는 신호 레벨 수를 나타내며, log2L은 비트당 전달할 수 있는 정보의 양을 나타냅니다. 이 방정식은 최대 데이터 전송 속도를 계산하는 데 사용되며, 채널 대역폭과 신호 레벨 수에 따라 데이터 전송 속도를 결정하는 중요한 요소 중 하나입니다. 단, 신호 레벨을 너무 많이 사용하면 정확도가 저하됩니다. 이는 noiseless channel 이라고 생각했을 때 사용한다.

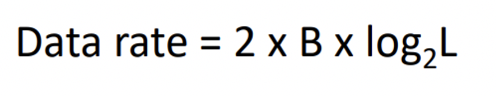
(B : bandwidth, L : number of signal levels)

→ 계산문제에서 예를 들어 L level 수가 98.7이 나왔어도 2의 배수여야 하므로 올림을 해서 64< 98.7 < 128 이므로 128 levels를 가져야 한다!

→ 신호 레벨의 수는 2의 거듭제곱이어야 합니다. 따라서 128 레벨 (280kbps)이 필요합니다. 이는 265kbps를 전송하기 위해 20kHz 대역폭의 노이즈 없는 채널에서 사용해야 하는 최소한의 레벨 수입니다. 이는 이진수 체계에서 각 비트가 2가지 가능한 상태 (0 또는 1)를 가지기 때문입니다. 따라서 레벨 수는 2의 거듭제곱이어야 합니다.

Shannon Capacity

Maximum bit rate in a noisy channel.

특정한 대역폭과 특정한 신호 대 잡음 비율(SNR)에서 전송 가능한 최대 데이터 전송 속도를 의미합니다. 채널 대역폭과 SNR이 주어졌을 때 채널에서 전송 가능한 최대 비트 전송률을 계산하는 공식으로 구할 수 있습니다. 이론적인 한계로, 실제로는 신호 처리 및 채널 조건에 따라 다르게 나타날 수 있습니다.

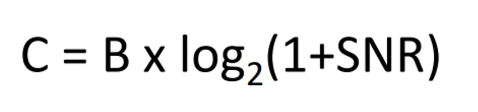
(C: capacity (maximum bit rate), B: bandwidth)

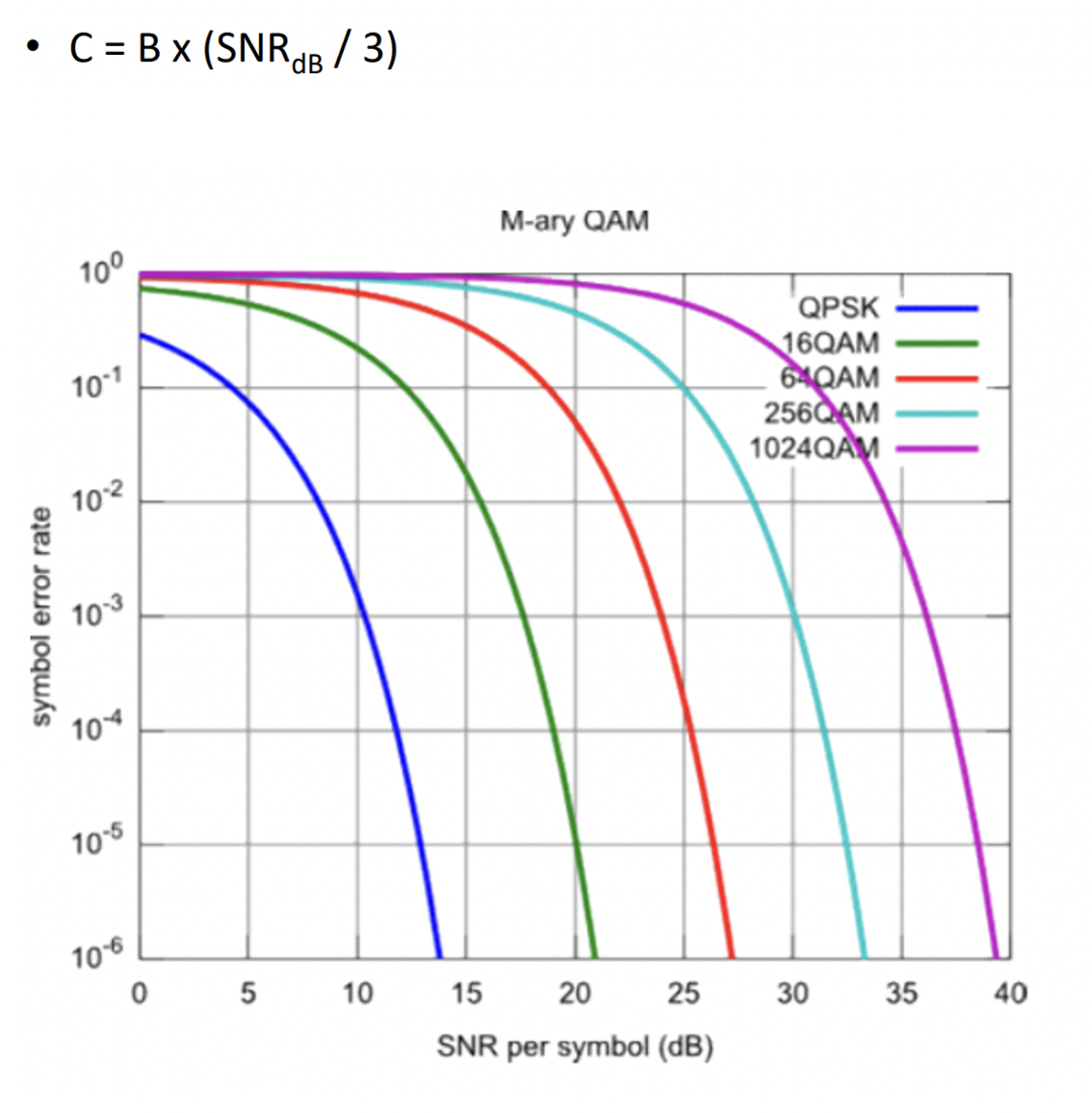
→ SNR이 높으면 전송속도 빨라짐 근데 에러도 많아짐

왜냐하면 전송속도를 빠르게 하기 위해서 신호를 많이 넣기 때문!

→ SNR이 0 이면 channel을 통해서 아무런 데이터도 보내거나 받지 못함!

→ SNR이 너무 높으면 1+SNR = SNR 이므로

Performance

Bandwidth

1. The size in frequency domain of a channel (Hz) 채널이 전송할 수 있는 주파수 대역폭
2. The maximum bit rate (bps = bits/second) 채널을 통해 전송될 수 있는 최대 비트 수를 초당(bps)으로 측정

대역폭(bandwidth)과 비트 전송률(bit rate)는 서로 관련이 있습니다. 대역폭은 채널이 전송할 수 있는 주파수 대역폭을 의미하며, Hz 단위로 측정됩니다. 반면에 비트 전송률은 채널을 통해 전송될 수 있는 최대 비트 수를 초당(bps)으로 측정한 것입니다.

Shannon-Hartley 정리에 따르면, 최대 전송 속도는 C = B * log2(1+SNR)로 계산됩니다. 여기서 B는 대역폭을 나타내며, SNR은 신호 대 잡음비(signal-to-noise ratio)입니다. 따라서 대역폭과 비트 전송률 사이의 관계는 다음과 같습니다.

Bit Rate = B * log2(1+SNR)

여기서 대역폭은 Hz 단위로 측정되므로, 비트 전송률을 계산하려면 대역폭을 bps 단위로 변환해야 합니다. 이를 위해서는 대역폭에 로그를 취한 후, 결과에 S/N 값을 더한 다음, 2를 거듭제곱해야 합니다. 즉, 다음과 같이 계산할 수 있습니다.

Bit Rate = B * log2(1+SNR) (bps) → 이거 수정하기

Throughout

• 제대로 데이터를 받은 것에 대한 속도 The actual data transfer rate(bps)
  
• Throughout < Bandwidth (단위는 같음)

→ Throughout은 제대로 받은 것만 취급하므로 bandwidth보다 클 수 없음

일정 시간 동안 전송되는 데이터 양의 총량을 나타냅니다. 즉, 일정 시간 동안 전송되는 데이터 양을 초당 비트 (bits per second, bps)으로 나눈 값이 throughout가 됩니다. 이는 네트워크의 대역폭, 지연 시간, 전송 프로토콜 등과 같은 다양한 요소에 영향을 받을 수 있습니다. 일반적으로, 높은 throughout를 유지하기 위해서는 높은 대역폭과 낮은 지연 시간이 필요하며, 전송 프로토콜의 최적화 및 데이터 압축 등과 같은 기술적인 요소도 고려되어야 합니다.

Delay 지연시간

• 메시지의 송신지에서 첫 번째 비트가 떠나는 시간부터 수신지에서 마지막 비트를 받는 시간까지의 경과 시간을 의미합니다.
• delay는 작을수록 좋음
• 따라서, 전송 지연 (transmission delay), 전파 지연 (propagation delay), 대기 지연 (queuing delay) 및 처리 지연 (processing delay)을 합한 값이 전체 딜레이 (delay)가 됩니다.

1. Transmission delay(전송 지연): 메시지의 첫 번째 비트가 출발지를 떠나서 마지막 비트가 출발지를 떠날 때까지 걸리는 시간입니다. (데이터 비트가 송신자에서 전송 매체로 전송되는 데 걸리는 시간)
2. Propagation delay(전파 지연): 비트가 출발지에서 목적지까지 이동하는 데 걸리는 시간입니다. 이는 비트가 이동하는 거리와 이동 속도에 의해 결정됩니다. (데이터 비트가 전송 매체를 통해 전파되는 데 걸리는 시간)
3. Queuing delay(대기 지연): 패킷 전송 시 경로 상에 있는 패킷 처리 대기열에서 대기하는 시간입니다. 이는 다른 패킷들이 처리되는 속도와 패킷 크기에 따라 달라집니다. (라우터나 스위치와 같은 네트워크 장비에서 발생하는 지연 시간)
4. Processing delay(처리 지연): 시스템이 메시지를 처리하는 데 걸리는 시간입니다. 이는 메시지의 길이와 처리 능력에 따라 달라집니다. (네트워크 장비에서 발생하는 데이터 처리 시간)

💡 Delay = transmission delay + propagation delay + queuing delay + processing delay 💡 Propagation time = distance / speed of signal 💡 Transmission time = message size / bandwidth

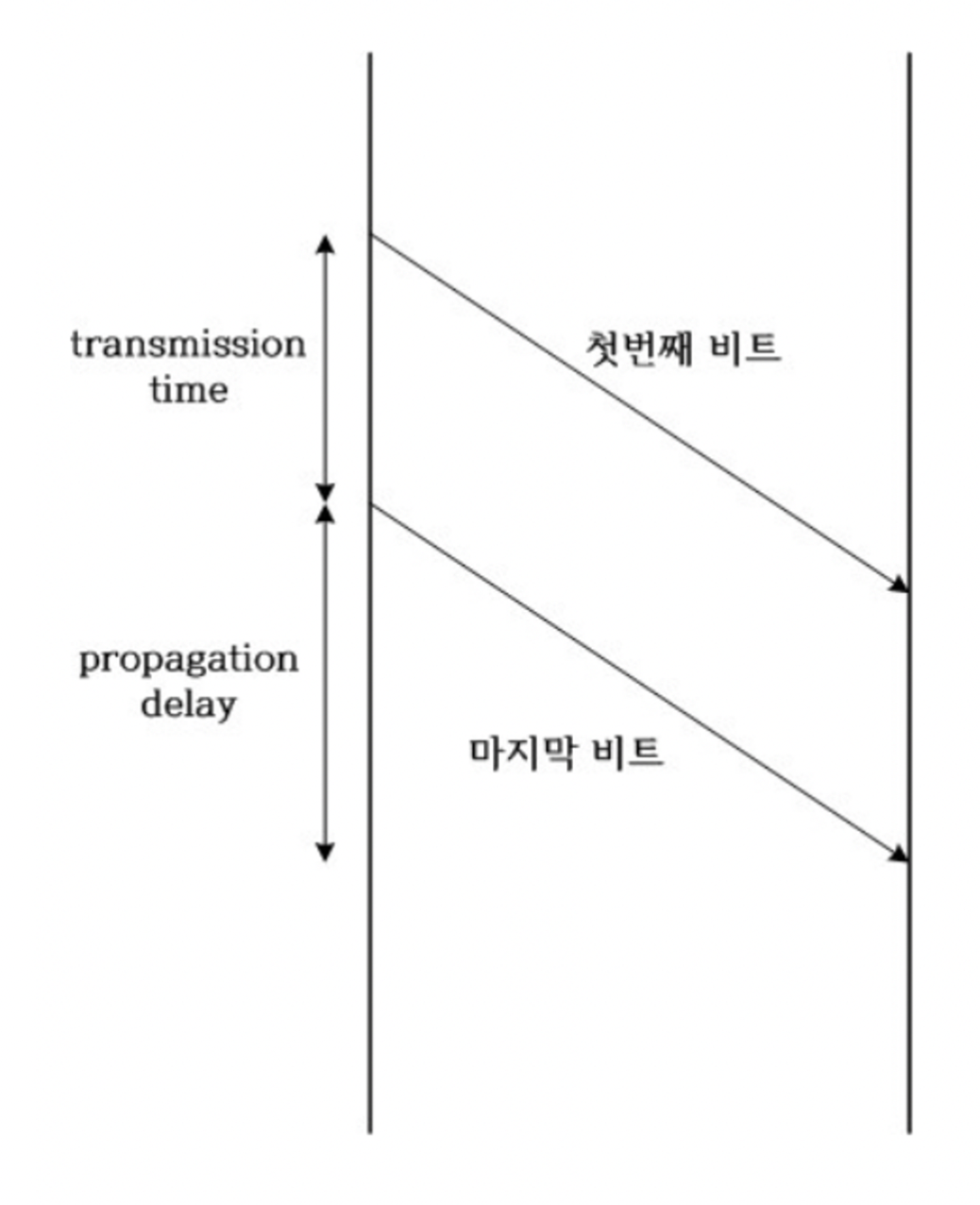
• if message is short and the bandwidth is large → Propagation time is the dominant factor
  
• if message is long and the bandwidth is small → Transmission time is the dominant factor
  

Bandwidth-Delay Product

Bandwidth-delay product represents the “volume” of the channel.

채널의 "용량" 즉, 데이터 전송 시간과 데이터 전송량을 나타내는 지표입니다. 이는 데이터가 네트워크에서 전송될 때, 채널의 대역폭(Bandwidth)과 전파지연(Propagation Delay)의 곱으로 계산됩니다.

예를 들어, 대역폭이 1Mbps이고 전파지연이 100ms인 채널의 Bandwidth-delay product는 1Mbps * 100ms = 100Kbits 입니다. 이 값은 한 번에 채널을 통해 전송 가능한 데이터 양의 상한선(최소한의 대역폭)을 나타내며, 이 값을 초과하는 데이터 양을 전송하려면 채널 이용 시간이 더 필요해집니다.

→ How much data can be fit into the channel between sender and receiver

💡 Bandwidth-delay product = Bandwidth x Propation Delay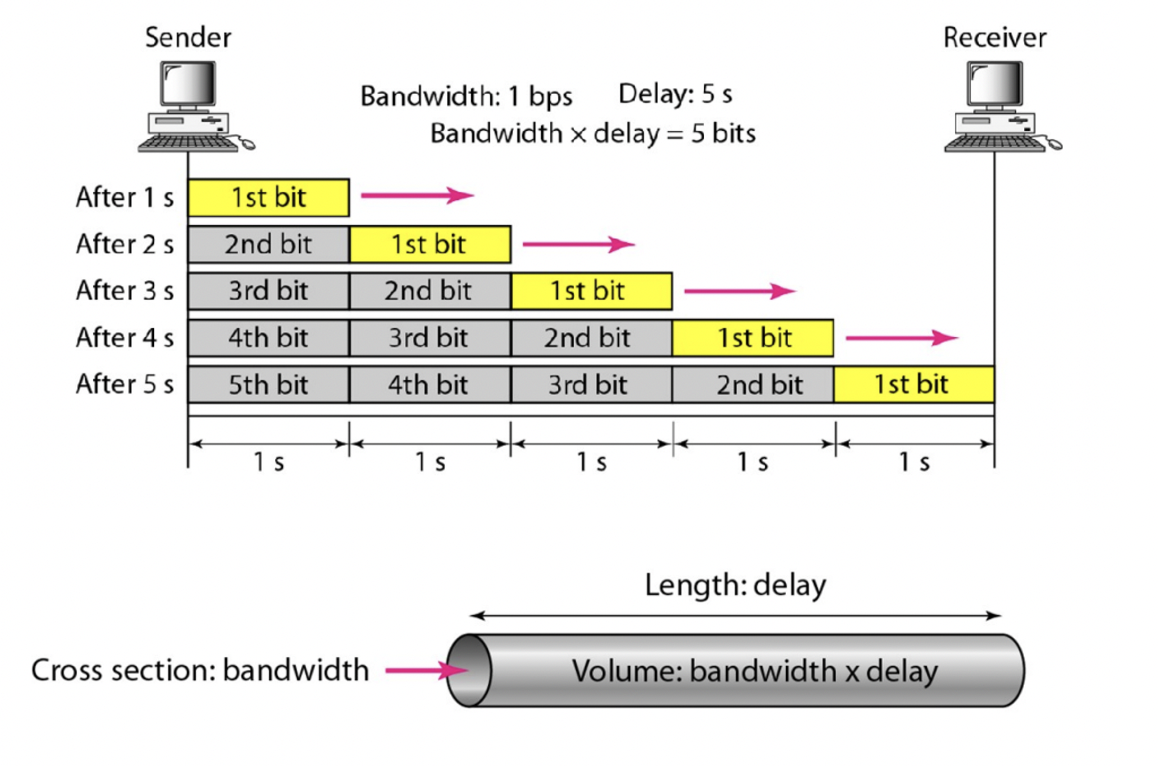

계산문제

💡 주파수(frequency) = 1 / 주기(period) 주기(period) = 1 / 주파수(frequency) 💡 Degree : 0 - 360도 Radian : 0 - 2 pi

ex) 90도 = 1/2 pi

180도 = pi

270도 = 3/2 pi

360도 = 2 pi

💡 wavelength = propagation speed x period = propagation speed / frequency

파장 = 전송 속도 x 주기 = 전송 속도 / 주파수

ramda = c / f

💡 bandwidth(대역폭) = 최대 주파수(f_max) - 최소 주파수(f_min) 💡 2^n개의 level → n개의 bit 정보

level = 2^bit수

💡 bit수 = log2 level 💡 **bps/2 = Hz** 💡 전송속도 bit rate : bps = bits/second 💡 Baseband Transmission은 **디지털 신호를 변조하지 않고 직접 전송**하는 방법입니다. 이 방법을 사용하면 **원래 디지털 신호와 거의 동일한 신호를 전송**할 수 있습니다. 그러나 **실제로는 사용 가능한 대역폭이 제한**되기 때문에 **전송되는 신호는 원래 신호의 근사치**일 수밖에 없습니다.

이때 사용 가능한 대역폭이 더 넓을수록, 전송되는 신호는 원래 신호에 더 가까워집니다. 왜냐하면 더 넓은 대역폭을 사용하면 더 많은 주파수 성분을 전송할 수 있기 때문입니다. 즉, 전송되는 신호는 원래 신호에 더 많은 주파수 성분을 포함하므로 원래 신호에 더 가까워집니다.

💡 N/2 Hz의 대역폭 bandwidth (N : 전송속도 transfer rate, bit rate) bandwidth = N/2 💡 baseband transmission에서 필요한 대역폭이 전송 속도에 비례한다.

더 많은 대역폭은 더 나은 근사치를 제공하여 더 높은 정확도를 얻을 수 있습니다. 즉, 대역폭이 더 넓을수록, 신호가 더 많은 원래의 정보를 포함하게 되므로, 전송 속도가 높아질수록 더 많은 대역폭이 필요하게 됩니다.

💡 baseband transmission : analog를 digital로 안바꾸고 직접 전송 band-pass channel modulation : digital을 analog로 바꿔서 전송하고 demodulation해서 analog를 digital로 바꿔서 데이터를 읽음 💡 Baseband vs Broadband

• Baseband와 broadband는 데이터를 전송하는 방법 중 두 가지입니다.
• Baseband는 디지털 신호를 그대로 전송하는 방법입니다. 따라서, 신호가 저주파에서 전송되며, 전송 대역폭이 적은 것이 특징입니다. → baseband transmission
• Broadband는 아날로그 신호를 변조하여 전송하는 방법입니다. 변조(Modulation)란, 기본적으로 아날로그 신호를 디지털 신호로 바꾸는 과정으로, 이 과정에서 신호는 고주파 신호로 변환됩니다. 따라서, 전송 대역폭이 넓은 것이 특징입니다. → bandpass transmission
• 두 방법의 가장 큰 차이점은 전송 대역폭의 차이입니다. Baseband는 저대역폭을 사용하므로 전송 속도가 느리지만, 신호의 왜곡이 적고 오류가 적습니다. 반면, Broadband는 고대역폭을 사용하므로 전송 속도가 빠르지만, 신호의 왜곡과 오류가 많을 수 있습니다.

💡 dBm = 10 log10 (P/1mW) 💡 1mW = 0dBm = 10log10 1 = 10 x 0 = 0

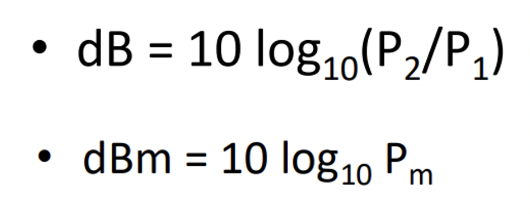
10mW = 10dBm = 10log10 10 = 10 x 1 = 10

100mW = 20dBm = 10log10 100 = 10 x 2 = 20

1000mW = 30dBm = 10log10 1000 = 10 x 3 = 30

200mW = 23dBm = 10log10 200 = 10 x (2 + 0.3) = 23 (log2 = 0.3)

40000mW = 46dBm = 10log10 40000 = 10 x (4 + 0.6) = 46 (log4 = 0.6)

💡 Signal-to-Noise Ratio SNR = signal power / noise power 💡 SNR = 10^(SNRdB/10) 💡 SNR dB = 10log10 (signal power / noise power) 💡 SNR dB = 10log10 SNR 💡 Data Transfer Rate(Bit Rate)

• 데이터 전송률은 세 가지에 의존한다.
  1. Bandwidth
  2. Number of signal levels
  3. Channel quality(noise level)

💡 Nyquist equation→ noiseless channel Date rate = 2 x B x log2 L (B:bandwidth, L: number of signal levels) → signal level이 너무 많으면 accuracy 감소

💡 Shannon Capacity : Maximum bit rate in a **noisy channel.**

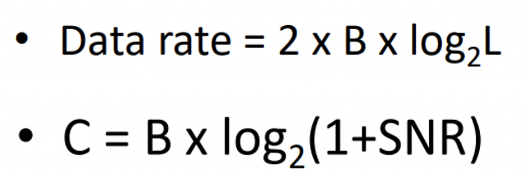
**특정한 대역폭과 특정한 신호 대 잡음 비율(SNR)에서 전송 가능한 최대 데이터 전송 속도

C = B x log2 (1+SNR)

(C: capacity, maximum bit rate, bps)
(B: bandwidth,Hz)**

💡 → **SNR이 높으면 전송속도 빨라짐** 근데 **에러도 많아짐**

왜냐하면 전송속도를 빠르게 하기 위해서 신호를 많이 넣기 때문!

→ SNR이 0 이면 channel을 통해서 아무런 데이터도 보내거나 받지 못함!

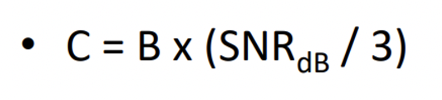
→ SNR이 너무 높으면 1+SNR = SNR 이므로 SNRdB/3 으로 계산!!

💡 Bandwidth

1. The size in frequency domain of a channel (Hz) 채널이 전송할 수 있는 주파수 대역폭
2. The maximum bit rate (bps = bits/second) 채널을 통해 전송될 수 있는 최대 비트 수를 초당(bps)으로 측정

💡 Throughout

• 제대로 데이터를 받은 것에 대한 속도 The actual data transfer rate(bps)
  
• Throughout < Bandwidth (단위는 같음)

💡 **Transmission delay(전송 지연)**: 메시지의 첫 번째 비트가 출발지를 떠나서 마지막 비트가 출발지를 떠날 때까지 걸리는 시간입니다. (데이터 비트가 송신자에서 전송 매체로 전송되는 데 걸리는 시간) → 1번이 출발할 때부터 10번이 출발할 때까지의 걸린 시간(총합)

Propagation delay(전파 지연): 한 비트가 출발지에서 목적지까지 이동하는 데 걸리는 시간입니다. 이는 비트가 이동하는 거리와 이동 속도에 의해 결정됩니다. (데이터 비트가 전송 매체를 통해 전파되는 데 걸리는 시간)
→ 1번이 출발해서 도착할때까지의 걸린 시간(개별)

💡 Delay = transmission delay + propagation delay + queuing delay + processing delay 💡 거리 = 시간 / 속도 💡 Propagation time = (거리) / (속도) 💡 Propagation time = distance / speed of signal 💡 Transmission time = message size / bandwidth 💡 amount of data(bit) = bandwidth of a link(bps=bit/second) x delay(s) **Bandwidth-delay product = Bandwidth x Propagation Delay**