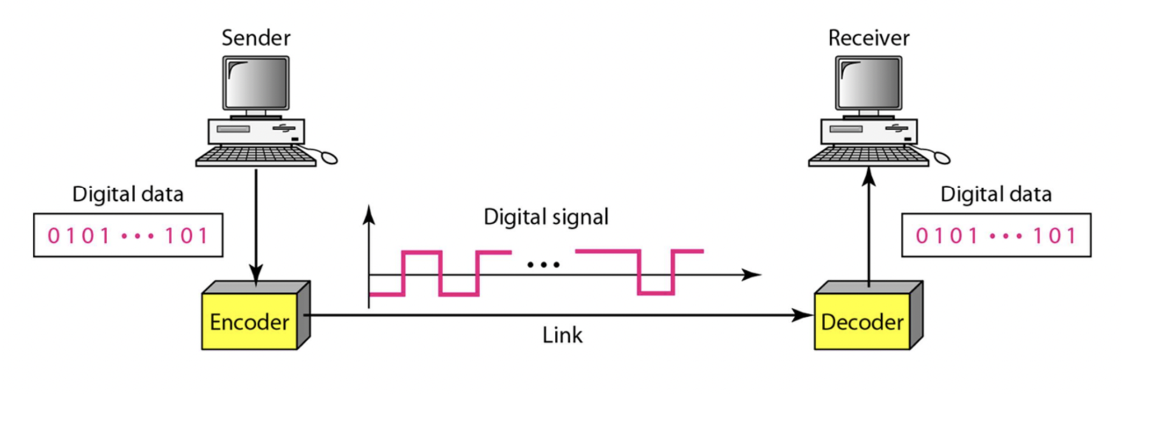
Digital-to-Digital Conversion
Line Coding
- Binary Data를 Digital signal로 바꿈
- 디지털 데이터를 전송 라인 상에서 전기 신호로 변환하는 과정을 의미합니다. 즉, 디지털 데이터를 전송하기 위해서는 이진 신호를 전송 라인 상에서 전기 신호로 변환해야 합니다. 이 때, 변환하는 방법을 line coding이라고 합니다.
- 대표적인 line coding 방식으로는 NRZ (Non-Return-to-Zero), Manchester Encoding, Differential Manchester Encoding, AMI (Alternate Mark Inversion) 등이 있습니다.
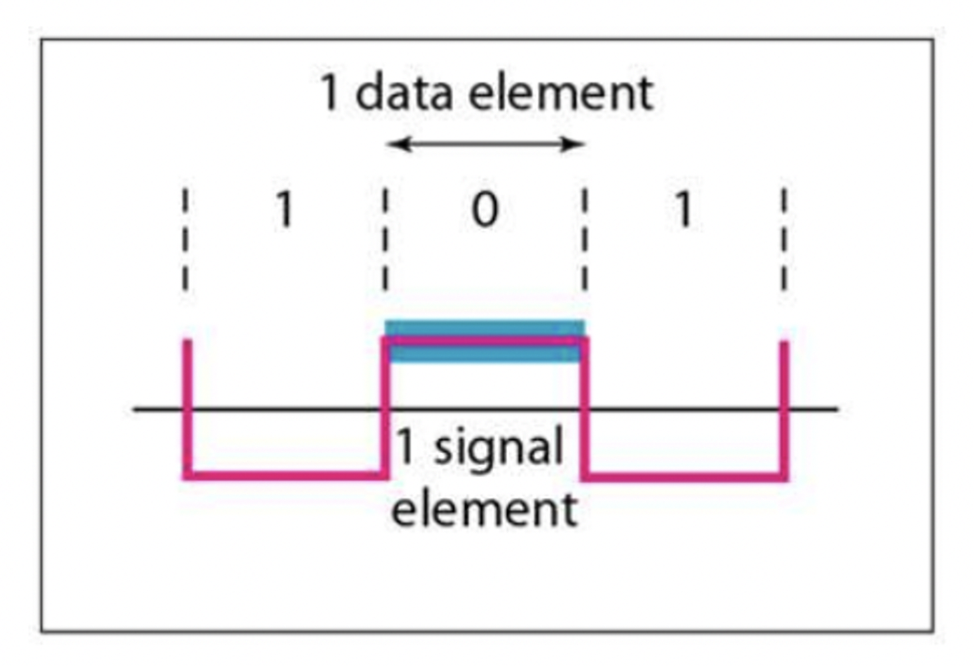
Data element & Signal element
Data element 디지털 요소
- digital data의 최소 단위 = bit
- 이진수 한 개 또는 여러 개로 구성
Signal element 신호 요소
- digital signal의 최소 단위
- 1개의 비트(bit)를 나타내는 디지털 신호의 한 요소
- 예를 들어, 1이나 0을 나타내는 이진 (binary) 디지털 신호에서, 각 신호는 1개의 비트를 나타내며, 이는 1개의 signal element와 같습니다. 만약 4개의 신호 상태(00, 01, 10, 11)를 가지는 디지털 신호를 사용한다면, 각각의 신호는 2개의 비트를 나타내며, 이는 2개의 signal element를 가지게 됩니다.
- 따라서, signal element는 데이터 전송에서 신호가 이동하는 가장 작은 단위이며, 이는 데이터 전송 속도와 관련된 매우 중요한 개념입니다.
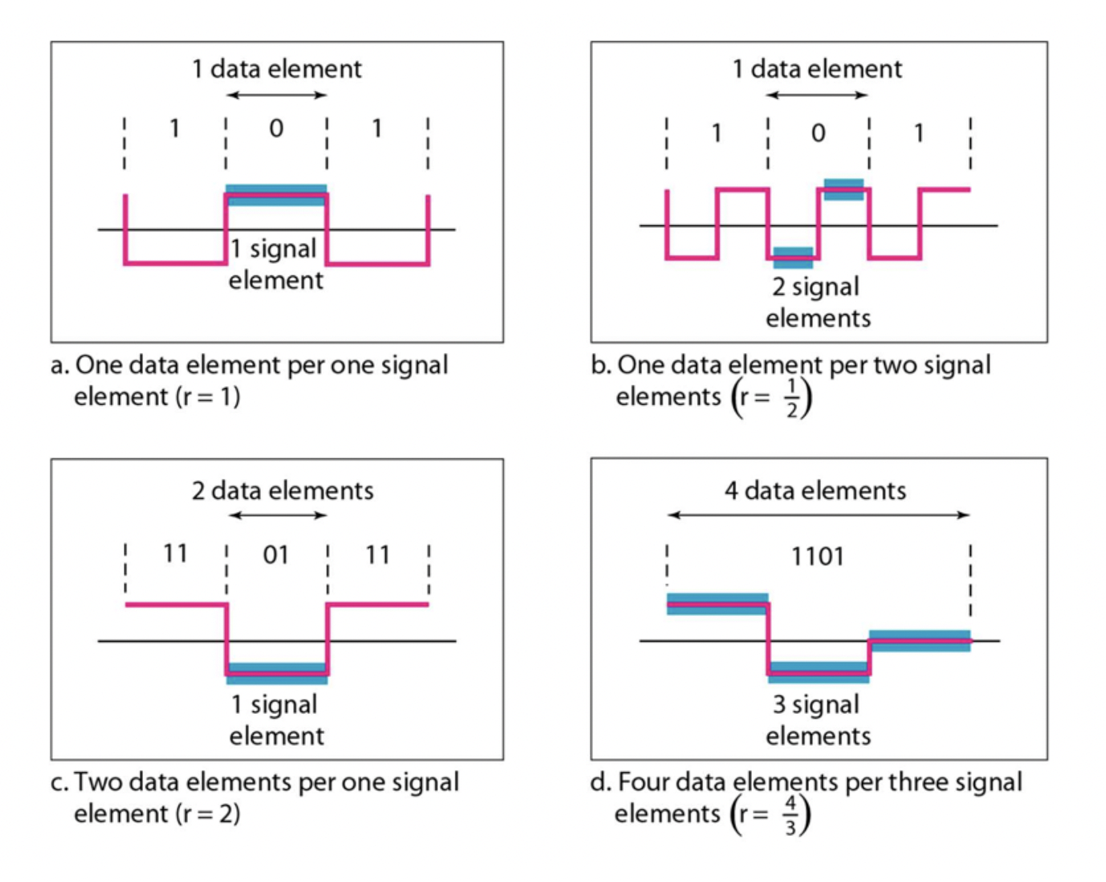
Units of Data and Signal Transmission
Data transmission rate
- 1초에 보내지는 data elements의 개수
- data element가 전송되는 속도
- 단위 : bps(초당 비트수)
- 데이터가 송수신되는 속도를 말합니다. 데이터 전송 속도는 일반적으로 초당 비트 수 (bps)로 측정됩니다. 이는 데이터가 송신자에서 수신자로 전송되는 데 걸리는 시간과 데이터 비트 수의 비율로 계산됩니다. 데이터 전송률은 네트워크 대역폭, 전송 거리, 라우팅 및 프로토콜 종류 등 여러 요인에 따라 다양합니다. 따라서 전송률이 높을수록 데이터가 빠르게 전송되고 처리되며, 네트워크의 전반적인 성능이 향상됩니다.
Signal transmission rate
- 1초에 보내지는 signal elements의 개수
- signal element가 전송되는 속도
- 단위 : baud (보)
- 초당 전송되는 신호(element)의 수 또는 속도를 말합니다. 이는 각각의 신호(element)가 나타내는 비트 수에 따라 결정됩니다. 예를 들어, 1초에 1000개의 신호(element)가 전송되고, 각각의 신호(element)가 4개의 비트를 나타내면, signal transmission rate는 4000bps가 됩니다. 이 값은 실제 데이터 전송 속도와 다를 수 있습니다. 데이터 전송 속도는 전송되는 데이터의 비트 수에 따라 결정되는 반면, signal transmission rate는 전송되는 신호(element)의 수에 따라 결정됩니다.
Digital-to-Digital Conversion Schemes
디지털 신호와 디지털 데이터 사이의 변환 방법을 나타냅니다. 디지털 데이터는 0과 1의 이진 코드로 표현되지만, 이진 코드로 표현된 디지털 데이터를 특정 디지털 신호로 변환해야 하는 경우가 있습니다. 예를 들어, 디지털 데이터를 광섬유 케이블을 통해 전송하기 위해서는 광섬유 케이블에서 사용되는 광신호로 변환해야 합니다. 이러한 디지털 데이터를 디지털 신호로 변환하는 과정을 디지털-디지털 변환(Digital-to-Digital Conversion)이라고 합니다. 이 과정에서는 디지털 데이터를 디지털 신호로 바꾸는 여러 가지 변환 방법을 사용할 수 있습니다. 예를 들어, Non-return-to-zero (NRZ), Manchester encoding, Bipolar encoding 등이 있습니다.
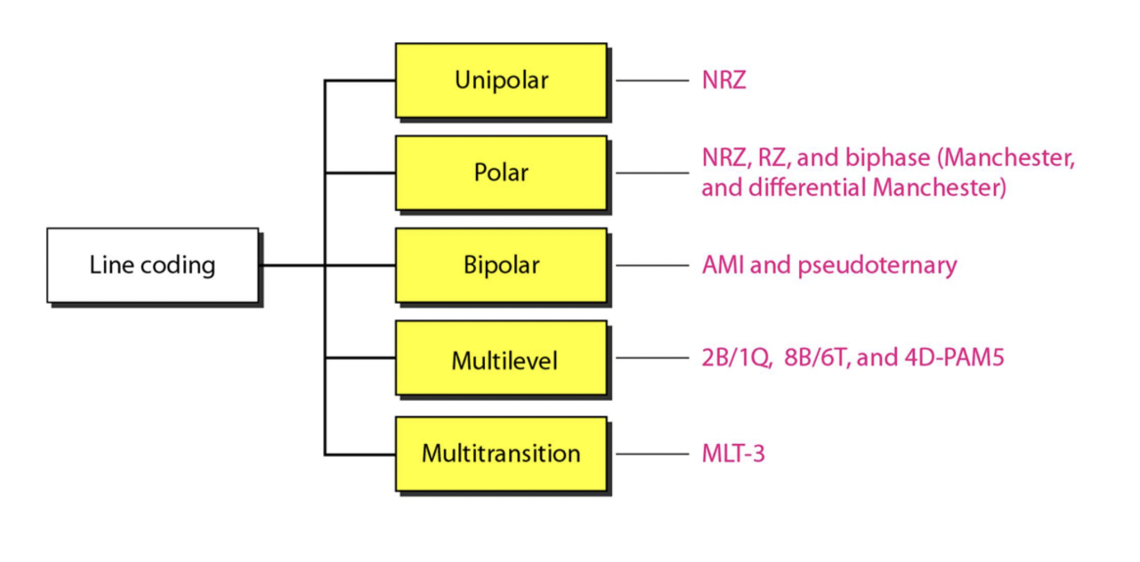
Unipolar Encoding
- 디지털 신호의 하나로, 전압의 양극성을 사용하여 디지털 데이터를 나타내는 방식입니다.
- Unipolar encoding에서는 0과 1을 나타내기 위해 전압의 한 극성을 사용합니다. 보통 전압의 positive 극성을 사용하여 1을 나타내고, 0은 0V를 사용합니다. 이 방식은 구현이 간단하고 신호의 구조가 단순하기 때문에 사용이 용이합니다.
- 하지만, Unipolar encoding에서는 데이터 전송에 사용되는 전압이 상수로 유지되기 때문에, DC offset 문제가 발생할 수 있습니다. 이는 신호의 평균값이 0으로 맞추어지지 않아, 오랜 시간 동안 전송할 경우 이를 받는 측에서 문제가 발생할 수 있습니다.
- Unipolar encoding은 데이터 전송 시, 0 또는 1의 두 가지 상태 중 하나를 0V 또는 양의 전압 값으로 표현하는 방식입니다. 따라서 "Encode one of the two binary data as 0V"는 0 또는 1 중 하나를 0V 값으로 인코딩하는 것을 의미합니다. 예를 들어, 0을 0V로 인코딩하고 1을 양의 전압 값으로 인코딩하는 방식입니다.
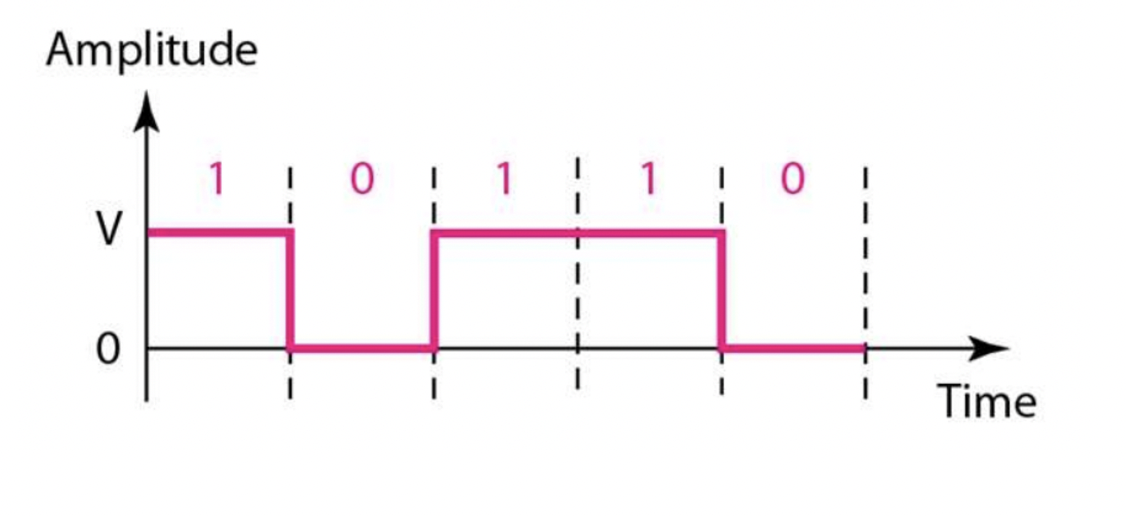
Unipolar NRZ(non-return-to-zero)
- 디지털 신호를 전송하기 위한 인코딩 방식 중 하나입니다. 이 방식에서는 0에 해당하는 바이너리 데이터를 표현하기 위해 0V의 전압을, 1에 해당하는 바이너리 데이터를 표현하기 위해 고정된 양의 전압 (예: 5V)을 사용합니다. 이전 신호 상태로 돌아가지 않기 때문에 "Non-Return-to-Zero"라는 이름이 붙여졌습니다. 이 방식은 간단하고 구현하기 쉽지만, 신호가 길어질수록 동기화 문제가 발생할 수 있습니다.
- Bit 1 → high volt
- Bit 0 → zero volt
- 두 개의 이진 데이터 (비트 0, 비트 1)를 인코딩하기 위해 +V, -V를 사용합니다.
- 하나의 이진 데이터를 표현하기 위해 하나의 전압 레벨만 사용하며 (예: 하나의 이진 값에 0V 사용), 다른 이진 데이터의 부재를 나타내기 위해 해당 전압 레벨을 사용하지 않습니다 (예: 다른 이진 값에 +V 또는 -V 사용). 예를 들어, +5V를 전압 레벨로 사용하고 두 개의 이진 데이터 (Bit 0, Bit 1)를 인코딩하는 Unipolar NRZ 방식에서 Bit 0은 0V로 표시되고 Bit 1은 +5V로 표시됩니다.
Polar Encoding
NRZ-L(Non-Return-to-Zero Level))
- 디지털 데이터를 아날로그 신호로 변환하기 위한 디지털-디지털 변환 방식 중 하나입니다. NRZ-L은 두 가지 전압 수준을 사용하여 이진 데이터를 인코딩합니다. NRZ-L 방식에서는 1의 비트가 있는 경우 전압을 양극성으로 변경하고 0의 비트가 있는 경우 이전 상태를 유지합니다.
- Bit 1 → 전압을 양극성으로 변경
- Bit 0 → 이전 상태를 유지
- 예를 들어, NRZ-L 방식을 사용하여 0101의 데이터를 전송하려면, 처음 비트 0은 이전 상태를 유지하기 때문에 이전 전압을 유지하고, 비트 1은 전압의 양극성을 변경하여 신호를 생성합니다.
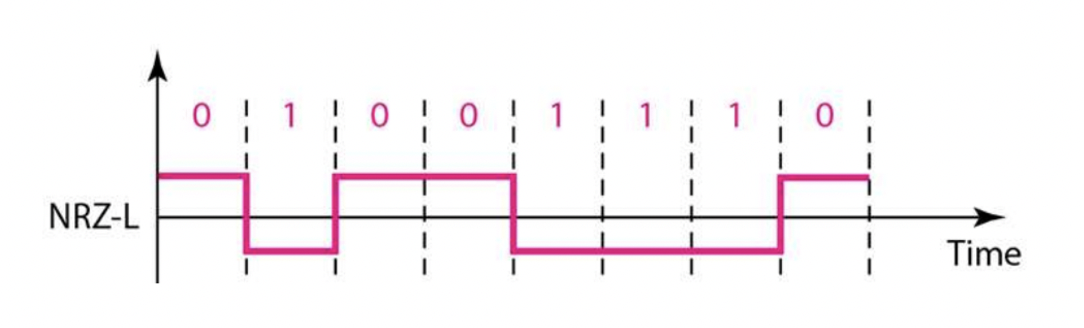
→ 여기서는 0이 high, 1이 low임
→ 0과 1을 high/low로 결정하는건 송수신자가 결정할 수 있음
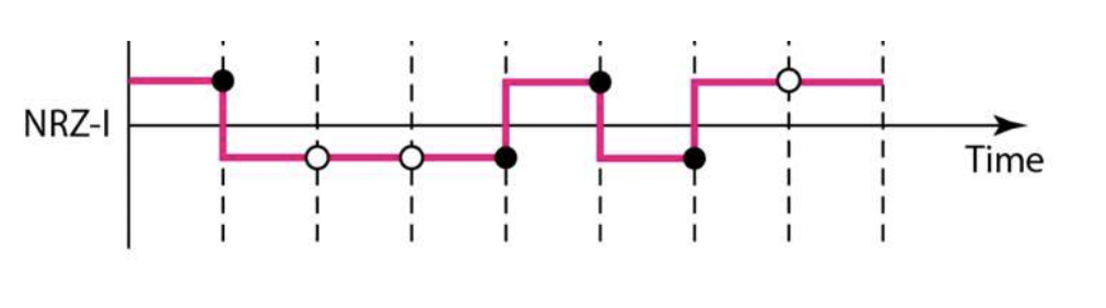
NRZ-I(Non-Return-to-Zero Inverted)
- 1과 0을 다른 신호로 표현하는 디지털 데이터 인코딩 방식 중 하나입니다. NRZ-I는 NRZ-L (Non-Return-to-Zero-Level)과 비슷하지만, 신호를 표현하는 방식이 다릅니다. NRZ-I는 1과 0이 연속으로 나타날 때마다 신호를 반전시키는데, 이전 신호의 상태에 따라 다음 신호를 표현합니다. 이전 신호가 0이었다면 다음 신호는 반전된 신호가 되며, 이전 신호가 1이었다면 다음 신호는 유지됩니다. 이 방식으로 인해 시간에 따른 신호 변화의 양을 줄일 수 있습니다.
- Bit 0 → 반전된 신호
- Bit 1 → 신호 유지
DC Component (안좋은거!)
- 시간 동안 신호의 평균값을 의미합니다. 이것은 신호가 양수와 음수 값을 균형적으로 가지지 않을 때 발생하며, 이는 신호의 대칭성을 깨뜨리고 신호의 전송과 저장을 복잡하게 만들 수 있습니다. 따라서 대부분의 디지털 통신 시스템에서 DC Component는 제거되어야 합니다.
- 신호가 일정한 수준으로 오랜 시간 동안 유지될 때 기준선 왜곡을 유발하며 클락 이동을 유발합니다.
- causes baseline wandering
- causes clock drift
1. Baseline wandering
- 데이터 신호의 디지털 값이 일정하게 유지되는 시간이 길어질 때 발생하는 문제입니다. 신호의 디지털 값이 일정하게 유지되면 신호의 평균값이 변경될 수 있습니다. 이러한 평균값의 변경은 신호의 정확한 디지털 값을 추정하기 어렵게 만들며, 신호의 파형이 손실될 가능성도 있습니다. 따라서 baseline wandering은 신호의 수신에 부정적인 영향을 미칠 수 있습니다.
- 수신기가 신호를 디코딩할 때는 기준선(baseline)을 기준으로 비트 0 또는 1을 결정합니다. 기준선은 수신된 신호의 평균 레벨입니다. 예를 들어, 만약 비트 0이 0V를 의미하고 비트 1이 12V를 의미한다면, 어느 시점 이후에는 평균 레벨이 대략 6V가 될 것입니다. 만약 긴 시간 동안 0의 연속 또는 1의 연속이 지속된다면, 기준선은 평균에서 벗어나기 시작하며, 디코딩할 때 문제가 발생할 수 있습니다.
→ 평균을 내서 평균보다 높으면 높은 준위, 낮으면 낮은 준위
→ 디지털 신호의 디지털 값이 비트 0이나 비트 1로 쭉 계속 지속된다면 기준선이 평균에서 벗어나 비트 0이나 비트 1의 값으로 가까워질것이다. 그러면 기준선에서 멀어지므로 문제가 생긴다.
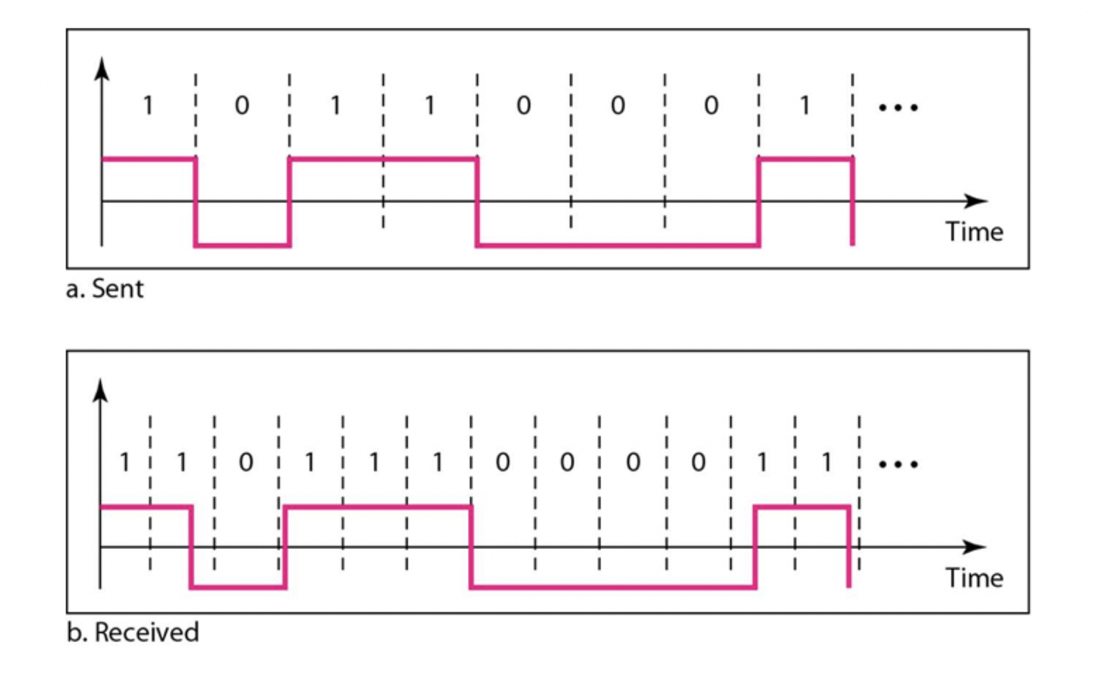
2. Clock Drift
- 시간 기반 신호의 속도 변화로 인해 신호와 수신 측의 클락 사이에 발생하는 차이를 의미합니다. 이는 수신 측에서 신호를 디코딩할 때 문제가 발생할 수 있습니다. 예를 들어, 클락 드리프트가 발생하면 수신기의 클락과 송신기의 클락이 동기화되지 않아 수신기가 보낸 신호를 올바르게 디코딩하지 못할 수 있습니다.
- 디바이스마다 clock 속도가 약간씩 다르다.
- 송신자와 수신자의 시간 불일치(time mismatch)는 수신자가 signal element 가 끝나는 시점을 모르기 때문에 디코딩 문제를 일으킬 수 있다.
Self Synchronization
- 수신 측에서 송신 측의 데이터를 기반으로 시간적인 정보를 자동으로 조정하여 수신 데이터의 시간적인 불일치를 해결하는 기술입니다. 이를 통해 수신 측은 송신 측의 clock과 정확하게 동기화되어 데이터를 올바르게 수신할 수 있습니다. 이 기술은 특히, 데이터 전송이 불규칙하게 발생하는 경우나 송신 측과 수신 측의 clock 속도가 다른 경우 유용합니다.
- 송수신기의 클록 속도가 서로 조금씩 다르더라도, 수신기는 신호의 변화가 자주 일어난다면 클록을 동기화할 수 있습니다. 코딩 방식이 신호의 변화를 강제하면, 이러한 방식을 "self synchronization" 속성을 가진 인코딩 방식이라고 합니다.
- NRZ-L과 NRZ-I는 자기 동기화 기능을 갖고 있지 않습니다. 이는 두 방식 모두 DC 컴포넌트를 생성할 가능성이 있기 때문입니다.
- 그러나 NRZ-I는 DC 컴포넌트를 생성할 가능성이 더 적습니다. 따라서 NRZ-L과 비교했을 때 NRZ-I가 baseline wandering과 Clock Drift 측면에서 더 나은 성능을 보입니다.
→ NRZ-I is better than NRZ-L in baseline wandering and clock drift
RZ(Return-to-Zero)
- 디지털 데이터를 전송하기 위한 디지털-디지털 변환 방식 중 하나입니다. 이 방식은 NRZ와는 다르게, 시간 구간을 같은 길이의 세그먼트로 분할하고, 각 세그먼트에서 1이 존재하는 경우에만 중간에 0으로 돌아갑니다. 이를 통해 신호의 baseline이 유지되어 DC component 문제를 해결할 수 있습니다. RZ 방식은 baud rate와 bit rate가 동일하고, 데이터의 0과 1을 구분하기 위해 두 개의 상태를 사용합니다.
- 데이터 비트를 인코딩할 때 두 개의 신호 요소를 사용합니다. 첫 번째 요소는 LOW 또는 HIGH 중 하나이며, 두 번째 요소는 0입니다. → 1. LOW/HIGH → 2. 0
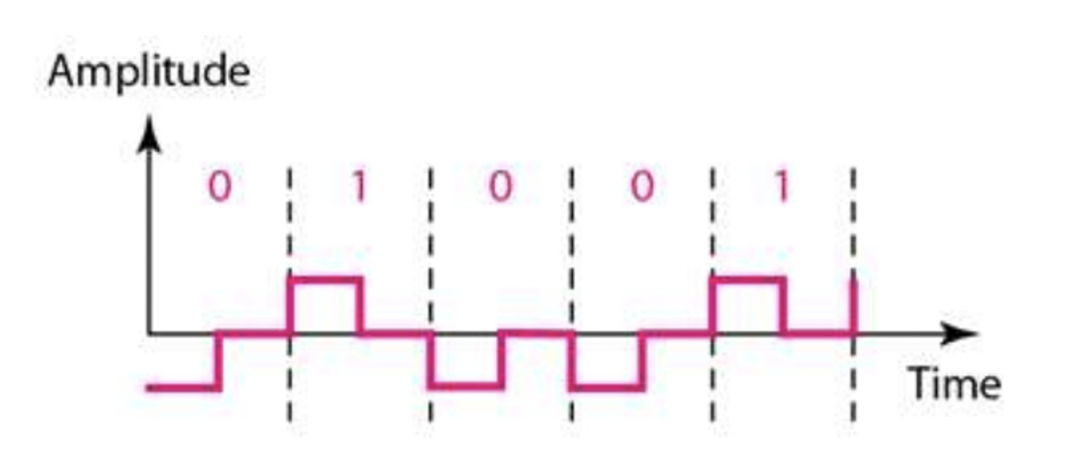
- RZ의 장점으로는 self-synchronization이 있습니다.
- 그러나 데이터 요소당 두 개의 신호 요소가 필요하므로 비트 전송률이 낮아지며, 두 배의 baud rate가 필요합니다. 또한, 세 개의 신호 레벨 (LOW, 0, HIGH)이 필요하므로 정확도가 낮아집니다. 마지막으로 baseline wandering 문제는 해결되지 않습니다.
→ 신호 레벨이 많아지면, 하나의 신호 레벨을 구분하기가 어려워지기 때문에 정확도가 낮아질 수 있습니다. 즉, 더 많은 신호 레벨을 사용하면 각 신호 레벨 간의 간격이 줄어들어, 잡음 등의 외부 요인으로 인해 각 신호 레벨을 정확하게 식별하기 어려워지기 때문입니다. 또한, 더 많은 신호 레벨을 사용하면 각 신호 레벨을 구분하기 위해 더 많은 비트가 필요하게 되어, 전송 비율이 낮아지는 단점도 있습니다.
⇒ 신호 레벨 증가 → 정확도 감소, 전송 비율 감소
Manchester, differential Manchester
- Manchester encoding과 Differential Manchester encoding은 둘 다 채널을 통해 디지털 데이터를 전송하기 위한 방식 중 하나입니다.
- Manchester와 Differential Manchester 모두 self-synchronization 특성을 가지고 있으며, baseline wandering 문제를 해결할 수 있습니다. 하지만 데이터를 인코딩하기 위한 신호의 레벨 변화가 빈번하게 일어나므로, bandwidth를 많이 차지하게 되며, 이로 인해 정확도가 낮아질 수 있습니다.
- RZ와 비교했을 때, 신호 레벨이 더 작은 편이며 데이터 비트마다 신호가 변경됩니다. RZ와 마찬가지로 이 방식도 두 배의 baud rate를 필요로합니다. 그러나 DC 구성 요소가 없으므로 baseline wandering이 없으며, 송수신기의 클럭 속도 차이로 인한 clock drift도 없습니다. → No DC component → No baseline wandering → No clock drift
Manchester Encoding
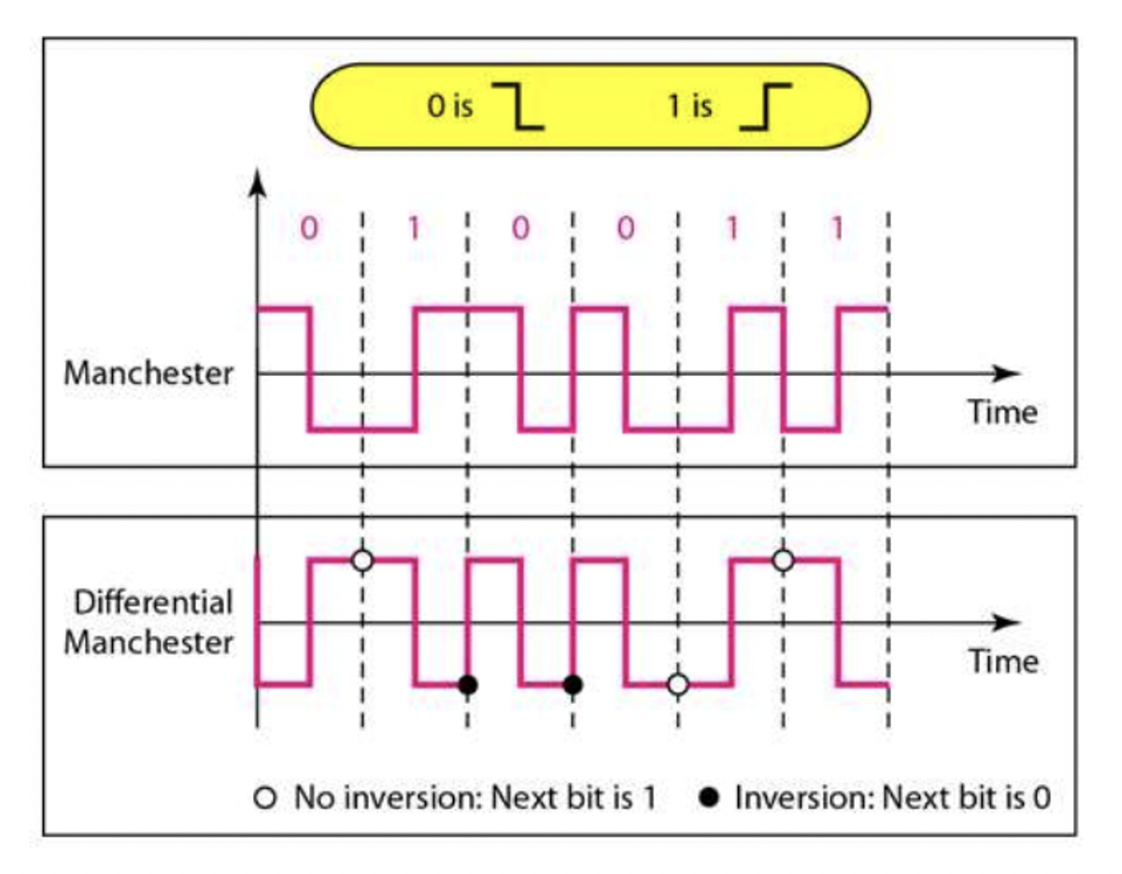
- 하나의 클럭 주기 동안에 데이터 비트를 두 부분으로 분리합니다. 이때, 데이터 비트가 1일 경우 첫 번째 부분은 LOW 신호, 두 번째 부분은 HIGH 신호로 인코딩됩니다. 그리고 데이터 비트가 0일 경우, 첫 번째 부분은 HIGH 신호, 두 번째 부분은 LOW 신호로 인코딩됩니다.
- Bit 1 : 1. LOW, 2. HIGH
- Bit 0 : 1. HIGH, 2. LOW
Differential Manchester Encoding
- 데이터 비트와 클럭의 변화를 함께 이용하여 인코딩합니다. Differential Manchester encoding에서는 클럭의 변화를 이용하여 현재 데이터 비트와 이전 데이터 비트를 구분합니다. 따라서, Manchester encoding과는 달리, 데이터 비트 값이 무엇이든 간에 항상 두 번의 클럭 주기 동안에 데이터 비트를 인코딩합니다.
BIpolar Encoding
- 0과 1 둘 중 하나의 바이너리 데이터를 0으로 인코딩하고, 나머지 하나의 데이터는 양수와 음수의 두 신호 요소를 사용하여 인코딩하는 방식입니다. 이 인코딩 방식에서는 신호 요소가 0인 시간이 길어질 때마다 신호 요소의 극성이 반전됩니다. 이를 이용해 신호가 길어져도 Clock drift와 baseline wandering 문제를 방지할 수 있습니다.
- Bipolar AMI (Alternate Mark Inversion) encoding은 가장 흔하게 사용되는 bipolar encoding 방식 중 하나입니다.
- 이진 데이터 중 하나는 0으로 인코딩되고, 나머지 하나는 LOW와 HIGH로 인코딩됩니다. → 0, LOW/HIGH
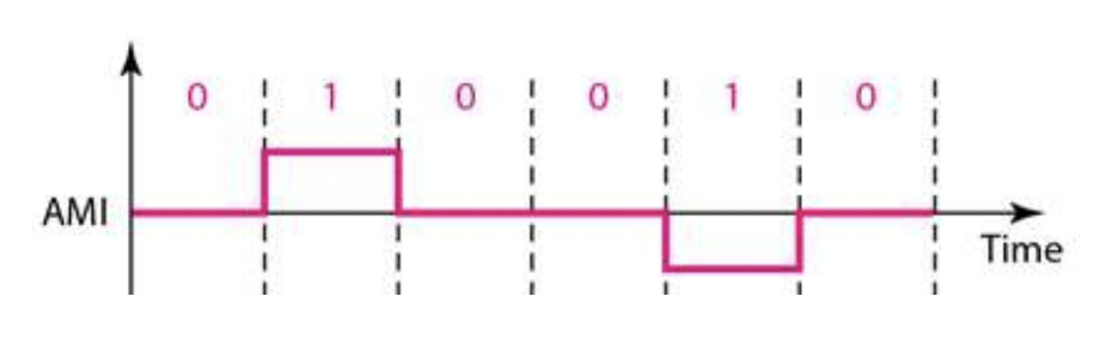
AMI(Alternate Mark Inversion)
- DC 구성 요소를 제거하기 위한 인코딩 방식입니다. 이 방식에서는 다음과 같이 데이터를 인코딩합니다:
- Bit 0 → 0V
- Bit 1 → 번갈아가며 LOW와 HIGH로 인코딩
- AMI는 데이터에 따라 신호의 높이가 번갈아가면서 변하므로 DC 구성 요소를 생성하지 않습니다. 또한, 쉽게 self-synchronization 할 수 있으며, baseline wandering과 clock drift 문제도 해결할 수 있습니다.
- DC component 제거
Pseudo-ternary encoding
- Bit 1 → 0V
- Bit 0 → 번갈아가며 LOW와 HIGH로 인코딩
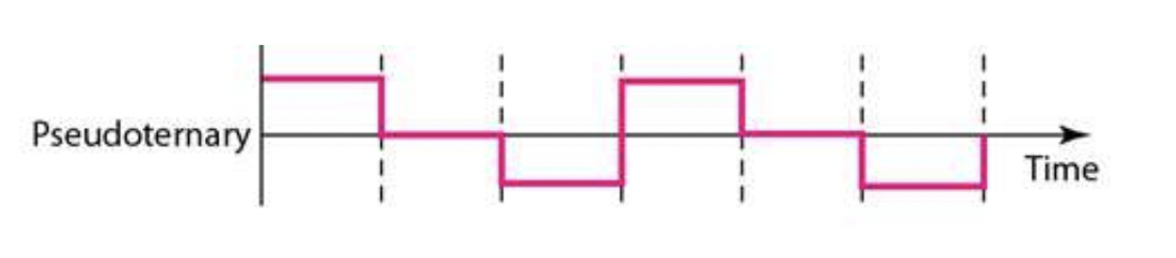
- DC component 생성
- Pseudo-ternary 인코딩은 신호가 LOW와 HIGH 사이를 번갈아가면서 변하기 때문에, 평균값이 항상 0V가 되도록 보장됩니다. 즉, AMI와 같이 0V를 기준으로 양극성이 번갈아가는 것이 아니기 때문에 DC 컴포넌트가 발생할 수 있습니다. 하지만, Pseudo-ternary 인코딩을 사용하는 경우, DC 컴포넌트는 필터링을 통해 제거할 수 있습니다.
- 1이 0V로 인코딩되는 대신 0 값이 신호가 번갈아가며 인코딩됩니다. 이 때, 0 값의 평균값은 0V가 아니라 0V에 가까운 값을 가지므로 DC 컴포넌트가 생성됩니다. 따라서, Pseudo-ternary encoding은 AMI처럼 DC 컴포넌트를 없앨 수 없습니다.
AMI vs Pesudo-ternary encoding
- 가장 큰 차이점은 비트 1의 표현 방식입니다.
- AMI (Alternate Mark Inversion)에서는 비트 1을 표현하기 위해 전압을 번갈아 가며 사용합니다. 즉, 비트 1은 번갈아가며 -V와 +V 사이를 왔다갔다 하면서 전송됩니다.
- Pseudo-ternary 인코딩에서는 비트 1을 표현하기 위해 전압을 0V로 유지합니다. 따라서, 비트 0은 번갈아가며 -V와 +V 사이를 왔다갔다 하면서 전송됩니다. → AMI ↔ Pseudo-ternary encoding
- AMI는 DC 컴포넌트를 제거할 수 있지만, Pseudo-ternary는 DC 컴포넌트가 생성됩니다.
- 또한, 신호 레벨이 3개 이상인 Multilevel 인코딩에서는 AMI가 사용됩니다.
Multilevel Encoding
Multilevel encoding은 하나의 신호 변환에서 두 개 이상의 신호 레벨을 사용하여 여러 비트를 동시에 인코딩하는 방식입니다. 이를 통해 전송 대역폭을 줄이고 데이터 전송 속도를 높일 수 있습니다.
Multilevel encoding에는 여러 가지 방식이 있습니다. 대표적인 예로는 2진 4종(Miller) 코드와 4진 5종 코드가 있습니다. 2진 4종 코드는 이전 비트의 신호 상태와 현재 비트의 신호 상태에 따라 4가지 상태 중 하나를 선택하여 인코딩합니다. 4진 5종 코드는 4개의 다른 신호 레벨을 사용하여 2비트씩 인코딩합니다. 이러한 방식을 통해 각각의 신호 전달이 더욱 효율적으로 이루어질 수 있습니다.
2B1Q
2B1Q는 2개의 비트가 하나의 신호 요소(signal element)로 인코딩되는 방식으로, 4개의 신호 레벨(Q)을 사용합니다. DSL에서 사용됩니다. 2B1Q는 신호 레벨을 4개로 제한하므로, 다른 멀티레벨 인코딩보다 더 낮은 대역폭을 요구하며, 더 높은 신호 노이즈와 인터피어런스에도 견딜 수 있습니다. 2B1Q는 주로 디지털 가입자 회선(DSL)에서 사용되며, 대역폭이 낮은 전화 회선에서 디지털 데이터를 전송하는 데 적합합니다.
8B6T
8B6T은 8 비트를 6개의 3단계 신호 요소로 인코딩하는 방식으로, 100BASE-4T에서 사용됩니다. 6개의 신호 요소는 다음과 같은 조건을 따릅니다.
• 요소에는 '+'와 '-'가 같은 수만큼 포함되어 있거나
• 요소에는 '+'가 '-'보다 하나 더 포함되어 있습니다.
또한 뒤이어 '+'가 하나 더 있는 신호 요소가 두 개 이어지면 두 번째 신호 요소는 반전됩니다.
MLT-3
이 방식은 LAN에서 사용됩니다.
- 다음 비트가 0이면, 신호 레벨은 변하지 않습니다.
- 다음 비트가 1이고, 현재 신호 레벨이 0이 아니라면, 신호 레벨은 0이 됩니다.
- 다음 비트가 1이고, 현재 신호 레벨이 0이라면, 신호 레벨은 가장 최근에 0이 아닌 레벨의 반전입니다.
장점 - 기본 주파수는 전송 속도의 1/4입니다.
단점 - 자기 동기화를 지원하지 않습니다 (긴 0의 문자열의 경우) - 세 가지 수준과 복잡한 전이 규칙을 사용하기 때문에 NRZ-I보다 복잡합니다.
Block Coding
블록 코딩은 m 개의 데이터 비트를 n 개의 데이터 비트 (블록 코드)로 변환합니다. 이것은 mB/nB 코딩이라고도 합니다. 여기서 m은 n보다 작습니다. 이러한 블록 코딩의 목표는 자기 동기화, 오류 검출 등입니다. 예를 들어, 8B/10B 블록 코딩은 8 개의 데이터 비트를 10 개의 블록 코드로 변환합니다. 이러한 블록 코딩은 고속 통신에서 매우 유용합니다.
4B/5B
4B/5B는 NRZ-I가 좋은 전송률(r = 1)을 보이지만 동기화 문제를 가지고 있다는 것을 보완합니다. 만약 0의 연속이 계속된다면, 동기화 문제가 발생할 수 있습니다. 4B/5B의 목표는 0의 연속을 피하는 것입니다.
4비트 데이터를 5비트 데이터로 변환하여, “0000”이 비트 스트림에 나타나지 않도록 합니다. 주어진 비트 스트림을 4B/5B 블록 인코딩으로 변환하는 문제입니다.
- 4비트 데이터: 0000, 0001, 0010, …, 1110, 1111
- 4비트 데이터를 5비트 블록 코드로 변환해야 함
- 5비트 중 첫 2비트는 적어도 하나의 '1'을 포함(01,10,11)해야 하며, 마지막 3비트는 적어도 하나의 '1'을 포함해야 함(000제외)
- 이전 조건을 만족하는 5비트 코드가 몇 개 있는지? 4비트 데이터 0000, 0001, 0010, ..., 1110, 1111이 주어졌습니다.
이를 5비트 블록 코드로 변환해야 합니다.
5비트 중 첫 2비트는 적어도 하나의 '1'을 포함해야 하며,
마지막 3비트는 적어도 하나의 '1'을 포함해야 합니다. 첫 번째 비트는 어떤 숫자를 선택하더라도 '1'이 포함되므로,
두 번째 비트는 '0'을 선택하거나 '1'을 선택할 수 있습니다.
따라서 두 번째 비트에는 2가지 선택지가 있습니다. 마지막 3비트에는 적어도 하나의 '1'이 포함되어야 합니다.
4비트 데이터에서 '0'을 선택하는 경우에는 두 가지 경우가 있습니다.
(예: 0000 -> 00001, 0000 -> 10000)
4비트 데이터에서 '1'을 선택하는 경우에는 4가지 경우가 있습니다.
(예: 0001 -> 00011, 0001 -> 10001, 0001 -> 01001, 0001 -> 00101)
동일한 방법으로 나머지 비트에 대해서도 경우의 수를 계산할 수 있습니다. 따라서 첫 번째 비트와 마지막 3비트를 조합하면 총 2 2 4 4 4 = 256개의 5비트 블록 코드가 생성됩니다. 이 블록 코드가 가능한 것인지 여부는 해당 블록 코드를 사용하여 데이터를 전송하고 수신 측에서 데이터를 복구할 수 있는지 여부로 확인할 수 있습니다.
- 이 블록 코딩이 가능한지 어떻게 증명할 수 있을까요?
Suppose signal is transmitted at 1M baud
• What is the data rate if NRZ-I + 4B/5B is used?
NRZ-I + 4B/5B:
4B/5B 코딩의 비트 전송률은 4개의 비트가 5개의 비트로 변환되기 때문에 원래의 비트 전송률보다 1.25배가 높습니다. 따라서 NRZ-I + 4B/5B 코딩을 사용하면 데이터 전송률은 1M baud x 5/4 = 1.25 Mbps가 됩니다.
• What is the data rate if Manchester Encoding is used?
Manchester Encoding:
Manchester 코딩은 각 비트를 두 개의 신호 요소로 전송하기 때문에 원래 신호의 전송률의 두 배가 필요합니다. 따라서 Manchester Encoding을 사용하면 데이터 전송률은 1M baud x 2 = 2 Mbps가 됩니다.
Scrambling
AMI 인코딩은 DC component를 제거하기 위해 LOW와 HIGH 신호를 교대로 사용합니다. 그러나, bit 0이 0V로 인코딩되기 때문에, 연속된 0이 계속되면 동기화 문제가 발생할 수 있습니다. 이를 해결하기 위한 방법 중 하나가 스크램블링입니다. 스크램블링은 오버헤드 없이 연속된 0을 제거하는 방식입니다.
B8ZS
B8ZS (Bipolar with 8 Zero Substitution)은 주로 북미에서 사용되는 인코딩 방식입니다.
B8ZS는 8개의 연속된 0을 감지하면 0의 위치를 변경합니다. 변경된 0은 Violation (V) 또는 Bipolar (B) 중 하나로 표시됩니다. Violation은 AMI 규칙을 위반하는 비-0 레벨을 의미하며, Bipolar은 AMI 규칙을 준수하는 비-0 레벨을 의미합니다.
예를 들어, 00000000을 인코딩 할 때, 000VB0VB로 인코딩됩니다. 이러한 방식으로 B8ZS는 DC 구성 요소가 없는 신호를 생성하면서 데이터를 전송할 수 있습니다.
💡 **B8ZS는 AMI 인코딩의 일종으로, AMI 인코딩에서 연속적으로 나타나는 0을 처리하기 위한 기술 중 하나입니다. AMI 인코딩에서는 0이 연속으로 나타날 경우 동기화 문제가 발생할 수 있습니다.** 💡 **B8ZS 인코딩은 다음과 같이 동작합니다. 먼저, 8개의 연속된 0을 찾습니다. 그리고 그 중에서 홀수 번째 0 다음에 나오는 신호의 극성(V)를 바꿔서, 0의 연속성을 깨뜨립니다. 이때 바뀐 극성(V)는 AMI 인코딩 규칙을 위반하는 값이어야 합니다. 그리고 짝수 번째 0 다음에 나오는 신호의 극성(B)는 AMI 인코딩 규칙을 따릅니다.** 💡 **따라서, 00000000은 8개의 연속된 0이므로, 그 중에서 홀수 번째 0 다음에 오는 신호의 극성을 바꿉니다. 이때 바뀐 극성(V)는 000VB0VB로 표현됩니다. 이렇게 함으로써, 0의 연속성을 깨뜨리고, 동기화 문제를 해결할 수 있습니다.**HDB3
HDB3 (High-Density Bipolar 3-Zero)은 북미 이외의 지역에서 사용되는 코딩 방식입니다.
HDB3은 B8ZS와 유사하게 AMI 인코딩 규칙을 따르면서도 0의 연속을 처리하기 위해 설계되었습니다. HDB3은 0000을 000V 또는 B00V로 대체합니다.
이전의 치환 후, 비-0 신호 요소의 수가 홀수 인 경우, 000V로 대체합니다. 예를 들어, 0000000000은 000V 000V 000V로 인코딩됩니다.
이전의 치환 후, 비-0 신호 요소의 수가 짝수 인 경우, B00V로 대체합니다. 예를 들어, 00000000은 B00V 000V로 인코딩됩니다.
이러한 대체는 신호의 밸런스를 유지하기 위해 수행됩니다. 즉, 양의 신호와 음의 신호의 수가 균형을 이루도록 합니다. 이를 통해 DC 바이어스를 제거하고 동기화 문제를 방지할 수 있습니다.
Ethernet
Ethernet은 컴퓨터 네트워크 기술 중 하나로, 컴퓨터나 기타 장치들을 서로 연결하여 통신할 수 있도록 해줍니다. 이더넷은 근거리 통신망(Local Area Network, LAN)에서 주로 사용되며, 케이블을 이용하여 연결된 컴퓨터들 간에 데이터를 전송합니다. 이더넷은 표준화된 규격으로, IEEE 802.3 표준으로 정의되어 있습니다.
이더넷은 CSMA/CD(Carrier Sense Multiple Access with Collision Detection) 방식을 사용하여 여러 기기가 동시에 데이터를 전송하지 않도록 조절합니다. 이 방식은 데이터를 보내기 전에 다른 기기들이 데이터를 전송 중인지 확인하여 충돌을 방지합니다. 또한, 이더넷은 다양한 전송 속도를 지원하며, 이더넷 케이블의 종류에 따라 최대 전송 속도가 결정됩니다. 일반적으로 이더넷은 10Mbps, 100Mbps, 1Gbps, 10Gbps 등의 속도를 지원합니다.
이더넷은 TCP/IP 프로토콜 스택과 함께 사용되어 인터넷과 같은 넓은 네트워크에 연결됩니다. 이더넷을 사용하면 여러 대의 컴퓨터와 기기들을 연결하여 데이터를 공유할 수 있으며, 데이터 전송 속도도 빠르게 할 수 있습니다.
Analog-to-digital conversion = Line coding
아날로그-디지털 변환(Analog-to-digital conversion, ADC)은 아날로그 신호를 디지털 신호로 변환하는 과정을 말합니다. 아날로그 신호는 연속적인 값을 가지며 시간에 따라 부드럽게 변합니다. 하지만 디지털 신호는 이산적인 값을 가지며 시간에 따라 갑자기 변합니다.
아날로그-디지털 변환 과정은 크게 샘플링(Sampling), 양자화(Quantization), 부호화(Encoding)의 세 단계로 이루어집니다.
- 샘플링: 아날로그 신호를 디지털 신호로 변환하기 위해서는 일정 시간 간격마다 신호를 측정해야 합니다. 이를 샘플링이라고 하며, 샘플링 주파수가 높을수록 원본 신호를 정확하게 재현할 수 있습니다.
- 양자화: 샘플링된 아날로그 신호의 값을 디지털 값으로 변환하는 과정입니다. 아날로그 신호는 연속적인 값을 가지기 때문에 무한히 많은 값을 가질 수 있습니다. 하지만 디지털 값은 이산적인 값을 가지기 때문에, 무한히 많은 값을 표현할 수 없습니다. 따라서 일정한 간격으로 값을 나눠서, 그 값을 대표하는 디지털 값으로 양자화합니다.
- 부호화: 양자화된 디지털 값을 디지털 신호로 변환하는 과정입니다. 부호화는 디지털 데이터를 전송하기 위한 필수적인 과정으로, 디지털 신호를 생성하는 방식에 따라 다양한 부호화 방법이 존재합니다.
PCM
Pulse Code Modulation (PCM)은 아날로그 신호를 디지털 신호로 변환하는 방법 중 하나입니다. 아날로그 신호를 주기적으로 샘플링하고, 각 샘플링 값에서 얻은 아날로그 값을 해당 비트 수만큼의 이진수로 변환하여 디지털 신호로 만듭니다. 이진수화된 샘플링 값은 PCM 신호로 압축되며, 이를 통해 아날로그 신호를 디지털 신호로 효과적으로 변환할 수 있습니다.
PCM은 대부분의 디지털 음향 시스템에서 사용됩니다. 예를 들어, CD 플레이어는 PCM 방식으로 디지털 신호를 생성하며, 이를 통해 오디오 신호를 저장하고 재생할 수 있습니다. 또한, 전화 통화나 무선 통신에서도 PCM 방식이 사용됩니다.
가장 기본적인 아날로그-디지털 변환 방법은 다음과 같습니다.
- 아날로그 데이터를 샘플링합니다.
- 샘플링 된 신호를 양자화합니다. 이는 연속적인 아날로그 값에서 디지털 값으로 변환하는 과정입니다. 양자화는 일정한 크기의 구간으로 신호를 나누고, 각 구간에서 가장 가까운 값을 선택하여 그 값으로 대체하는 것입니다.
- 양자화 된 신호를 디지털 비트 스트림으로 인코딩합니다. 이는 양자화 된 값들을 이진 코드로 표현하는 것입니다.
이렇게 변환 된 디지털 신호는 디지털 신호 처리나 저장 등에 이용될 수 있습니다.
Sampling
아날로그-디지털 변환에서 샘플링(Sampling)은 아날로그 입력 신호를 일정한 시간 간격으로 측정하여 디지털 신호로 변환하는 과정입니다. 이는 아날로그 신호를 연속적인 값을 가지는 함수로 간주하는 것에서 벗어나, 이산적인 값을 가지는 시간적인 신호로 변환하는 작업입니다.
아날로그 신호는 시간에 따라 연속적인 값을 가지며, 이를 디지털로 변환하기 위해서는 일정한 시간 간격으로 아날로그 신호를 샘플링하여 이산적인 값을 구해야 합니다. 이 과정에서 샘플링 주파수는 아날로그 신호의 최대 주파수보다 높아야 하며, 일반적으로는 나이퀴스트 샘플링 정리에 따라 샘플링 주파수는 최소 2배의 최대 주파수로 설정됩니다.
이렇게 샘플링된 값들은 양자화 과정을 거쳐 디지털 값으로 변환됩니다.
샘플링 주기(Sampling period)는 신호를 샘플링하는 간격을 말하며, 초 단위로 표현됩니다. 예를 들어, 1/8000초마다 신호를 샘플링하면, 샘플링 주기는 1/8000초가 됩니다.
샘플링 주기와 샘플링 비율(Sampling rate)은 서로 반비례 관계에 있습니다. 샘플링 비율은 초당 샘플링하는 횟수로 표현되며, 헤르츠(Hz) 단위로 측정됩니다. 예를 들어, 8000Hz의 샘플링 비율은 1초에 8000번의 샘플링을 의미합니다.
또한, 샘플링 주기와 샘플링 비율은 다음과 같은 관계가 성립합니다: 샘플링 주기 x 샘플링 비율 = 1입니다. 이 관계식은 샘플링 주기와 샘플링 비율 중 하나가 주어졌을 때, 다른 하나를 계산하는 데 사용될 수 있습니다.
💡 Sampling period x Sampling rate = 1 💡 나이퀴스트 정리는 아날로그 신호를 디지털로 샘플링할 때, 샘플링 주파수가 해당 신호의 최대 주파수의 2배보다 높아야 정확한 디지털 신호로 복원될 수 있다는 것을 말합니다. 이러한 이유는, 아날로그 신호의 최대 주파수를 넘는 부분은 디지털화될 때 왜곡이 발생하기 때문입니다. 따라서 나이퀴스트 정리는 디지털화된 신호의 질을 보장하기 위해 매우 중요합니다.Q) Telephone companies digitize voice by assuming a
maximum frequency of 4000 Hz. What is the
minimum sampling rate?
Nyquist 정리에 따르면, 신호의 최대 주파수의 두 배보다 높은 최소 샘플링 비율이 필요합니다.
전화 회사에서 음성을 디지털화하는 경우, 최대 주파수는 4000Hz로 가정됩니다. 따라서 최소 샘플링 비율은 다음과 같아야 합니다.
2 x 4000 Hz = 8000 Hz
따라서 전화 회사에서 음성을 디지털화하기 위해 필요한 최소 샘플링 비율은 초당 8000개의 샘플 또는 8kHz입니다.
💡 sampling rate = maximum frequency of the signal x 2Q) A complex low-pass signal has a bandwidth of
200kHz. What is the minimum sampling rate for this
signal?
나이퀴스트 정리에 따르면, 신호의 최대 대역폭의 적어도 두 배 높은 샘플링 속도가 필요합니다.
이 경우 신호의 대역폭은 200kHz이므로, 최소 샘플링 속도는 다음과 같습니다.
2 x 200kHz = 400kHz
따라서 이 신호의 최소 샘플링 속도는 초당 400,000 샘플 또는 400 kHz입니다.
quantizing
Quantizing(양자화)는 연속적인 아날로그 신호를 디지털 값으로 변환하는 과정 중 하나입니다. 이 과정에서, 연속적인 아날로그 신호를 일정한 간격으로 샘플링 한 후, 샘플 값들을 가장 가까운 디지털 값으로 근사화합니다. 디지털 값들은 미리 정의된 비트 수의 이진수로 표현됩니다.
Quantizing(양자화)의 정밀도는 비트 수에 따라 결정됩니다. 예를 들어, 8비트 ADC(Analog to Digital Converter)는 256개의 가능한 디지털 값으로 신호를 근사화할 수 있습니다. 더 많은 비트를 사용하는 ADC는 더 정밀한 근사화가 가능합니다.
하지만, quantizing(양자화)에 의해 정보 손실이 발생할 수 있습니다. 작은 신호 변화는 무시되고 반올림 또는 버림에 따라 디지털 값이 결정됩니다. 이러한 정보 손실을 최소화하기 위해, 적절한 비트 수와 quantizing(양자화) 기술이 선택되어야 합니다.
아날로그 신호를 디지털 신호로 변환하기 위해 우리는 샘플링 과정을 거치게 됩니다. 이 과정에서 샘플링된 신호는 최소 및 최대 진폭 사이의 어떤 값이든 가질 수 있습니다. 이렇게 되면 디지털 신호로 인코딩하기 위해 신호를 이산적인 신호 레벨로 양자화해야 합니다. 양자화란 연속적인 아날로그 신호를 이산적인 값으로 변환하는 과정을 말합니다. 이러한 과정을 통해 아날로그 신호를 샘플링된 값에서 양자화된 값을 가지는 디지털 비트 스트림으로 변환할 수 있습니다.
아날로그 신호가 Vmin부터 Vmax까지의 진폭을 갖는다고 가정해봅시다.
이때, (Vmin, Vmax) 범위를 D 크기의 L개의 구간으로 나눕니다.
D = (Vmax - Vmin) / L로 계산할 수 있습니다.
그리고 각 구간에 대해 양자화 코드를 할당합니다.
Quantizing(양자화)는 가능한 아날로그 신호의 진폭 범위를 유한한 수의 레벨로 나누고 각 레벨에 고유한 디지털 코드를 할당하는 과정입니다. 아날로그 신호를 양자화하는 단계는 다음과 같습니다:
- 아날로그 신호 진폭 범위를 결정합니다. 이 범위는 Vmin에서 Vmax까지 입니다.
- 사용할 양자화 레벨 수를 결정합니다. 이것은 L이라는 변수로 나타냅니다.
- 각 레벨의 크기를 계산합니다. 이것은 D라는 변수로 나타냅니다. D = (Vmax - Vmin) / L
- 각 레벨에 디지털 코드를 할당합니다. 예를 들어, 4개의 레벨을 사용하는 경우 다음 코드를 할당할 수 있습니다: 00, 01, 10 및 11.
- 양자화 과정에서 아날로그 신호는 각 레벨의 경계와 비교되며 해당하는 디지털 코드가 할당됩니다. 결과적으로 생성된 디지털 코드는 아날로그 신호를 디지털 도메인에서 나타내는 데 사용됩니다.
양자화 오차(Quantization Error)는 실제 값과 양자화된 값 사이의 차이를 말합니다. 이 오차의 크기는 양자화 단계 크기(D)의 절반(-D/2)보다 크거나 같고, D/2보다 작거나 같습니다.
양자화 레벨의 수가 증가할수록 양자화 오차는 감소합니다.
양자화 오차는 SNR(dB)에 영향을 미칩니다. SNR(dB)은 다음과 같이 표현됩니다:
💡 SNR(dB) = 6.02nb + 1.76dBnb : 여기서 n은 한 샘플당 비트 수를 의미합니다.
SNRdB는 신호 대 잡음 비율(Signal-to-Noise Ratio)을 데시벨(dB)로 표시한 값입니다. 이는 시스템에서 신호의 전력과 잡음의 전력 비율을 측정한 것입니다.
양자화에서 SNRdB는 다음 공식을 사용하여 계산할 수 있습니다:
SNRdB = 6.02nb + 1.76dB
- nb : 여기서 nb는 양자화에 사용되는 샘플 당 비트 수입니다.
예를 들어, 8 비트 샘플을 사용하는 경우, nb = 8이며 SNRdB는 다음과 같이 계산될 수 있습니다.
SNRdB = 6.02 x 8 + 1.76 - 8 = 49.92 dB
즉, 양자화 이후 신호 전력이 잡음 전력보다 거의 50 dB 높은 것으로, 신호의 품질이 양호한 것을 나타냅니다.
Q)
A telephone subscriber line must have an SNRdBabove 40. What is the minimum number of bits per
sample?
The minimum number of bits per sample required for a telephone subscriber line with an SNRdB above 40 can be determined using the following formula:
SNRdB = 6.02nb + 1.76dB - nb
where nb is the number of bits per sample.
Rearranging the formula, we get:
nb = (SNRdB - 1.76dB) / 6.02
Substituting SNRdB = 40, we get:
nb = (40 - 1.76) / 6.02 = 6.49
Therefore, the minimum number of bits per sample required for a telephone subscriber line with an SNRdB above 40 is 7 (rounded up from 6.49).
Q)
We want to digitize the human voice. The frequency
of human voice is between 0 and 4000Hz. What is
the bit rate, assuming 8 bits per sample?
To calculate the bit rate for digitizing the human voice, we need to consider the sampling frequency and the number of bits per sample.
Assuming a sampling frequency of 8000 Hz, which is the minimum for voice applications according to the Nyquist theorem, and 8 bits per sample, we can calculate the bit rate as follows:
Bit rate = sampling frequency × bits per sample
= 8000 Hz × 8 bits
= 64,000 bits per second
Therefore, the bit rate for digitizing the human voice with a sampling frequency of 8000 Hz and 8 bits per sample is 64,000 bits per second.
인간의 대화를 디지털화할 때 일반적으로 사용되는 표준 샘플링 주파수는 8000Hz입니다. 이는 나이키스트-섀넌 샘플링 이론에 따라 결정됩니다. 이 이론은 샘플링 주파수를 원래 신호의 최대 주파수의 두 배 이상으로 설정하면 해당 신호를 완벽하게 복원할 수 있다는 것을 보여줍니다. 대부분의 인간의 목소리 주파수 범위는 0~4000Hz 사이에 있으므로, 이를 고려하여 샘플링 주파수를 8000Hz로 선택합니다. 이렇게 함으로써 최대 주파수의 두 배 이상으로 샘플링 된 신호를 얻을 수 있으므로 인간의 목소리를 충분히 재현할 수 있습니다.
PCM decoder
PCM 디코더는 Pulse Code Modulation (PCM) 인코딩으로 압축된 디지털 오디오 신호를 원래의 아날로그 신호로 변환하는 장치입니다. PCM 인코딩은 아날로그 신호를 디지털 신호로 변환하기 위한 가장 일반적인 방법 중 하나입니다. PCM 인코딩은 아날로그 신호를 일정한 간격으로 샘플링하고, 각 샘플링된 값의 양자화 (Quantization)를 수행하며, 그 결과를 이진수로 변환하여 디지털 신호로 인코딩합니다.
PCM 디코더는 이진수 형태로 인코딩된 PCM 신호를 받아 각 샘플의 값에 해당하는 아날로그 신호를 생성합니다. 이를 위해, PCM 디코더는 인코딩 시 사용된 샘플링 주파수와 양자화 비트 수를 고려하여 샘플링 주기와 양자화 레벨 값을 계산합니다. 그런 다음, 이진수로 인코딩된 PCM 샘플 값을 다시 아날로그 신호로 복원하기 위해 D/A (Digital to Analog) 컨버터를 사용합니다. 이렇게 복원된 아날로그 신호는 소리로 들을 수 있습니다.
Delta Modulation은 이전 샘플과의 차이를 찾아 샘플링하는 방법으로, PCM과 달리 각 샘플의 신호 크기를 찾는 대신 각 샘플과 직전 샘플과의 차이를 찾습니다. Delta Modulation은 PCM보다 간단한 방법으로, 샘플링 주파수가 낮은 음성 신호를 디지털 신호로 변환할 때 유용하게 사용됩니다.
계산문제
💡 Baud rate(kbaud/sec) = signal element 수 × bit rate(kbps) 💡 Unipolar encoding (0,1) : Unipolar NRZ(non-return-to-zero)Bit 1 → high V
Bit 0 → 0 V
Bit 1→-V
Bit 0 → +V
Bit 1→ 유지
Bit 0 → 반전
⇒ Self synchronization으로 해결 가능!
💡 NRZ-I, NRZ-L → **self synchronization X, DC component O, baseline wandering O, clock drift O → transmission rate는 좋음** → NRZ-I가 DC component 생성할 가능성이 적으므로 NRZ-L보다 baseline wandering과 clock drift면에서 더 좋음 → NRZ-I is better 💡 Polar encoding : RZ(Return-to-Zero)first element → LOW / HIGH
second element → 0
→ self synchronization O
→ baseline wandering O
→ DC component O
→ 데이터 요소당 2개의 신호 필요 → lower bit rate
→ 신호 레벨이 3개(LOW,0,HIGH) → lower accuracy
→ signal이 많음 ⇒ bit rate, accuracy 모두 low
→ self synchronization O
→ base wandering X
→ clock drift X
→ DC component X
→ 데이터 인코딩 위한 신호 레벨 변화가 많으므로 bandwidth 많음 → low accuracy
💡 Bipolar encoding → 0과 1 중 하나의 이진 데이터를 0으로 인코딩 → 나머지 하나는 LOW/HIGH 💡 Bipolar Encoding : AMI (Alternate Mark Inversion) → DC component 제거하기 위해Bit 1 → LOW와 HIGH를 번갈아가며 ⇒ 한 번 1이 LOW였으면 그 다음 1은 HIGH
Bit 0 → 0V
문제 : Bit 0 → 0V로 인코딩되면 0이 지속돼서 self synchronization 안될 수 있음
→ 그래서 Scrambling을 사용해서 overhead없이 연속된 0 제거!
- 8개의 연속된 0 찾기
- 홀수번째 0 다음에 나오는 신호의 극성을 V로 변경
- 짝수번째 0 다음에 나오는 신호의 극성을 B로 변경
00000000 → 000VB0VB
Scrambling : HDB3(High-Density Bipolar 3-Zero)
→ 양의 신호, 음의 신호수가 균형을 이루도록
→ DC component 제거
→ 동기화문제 방지
→ non-zero가 홀수개 → 000V
→ non-zero가 짝수개 → B00V
→ non-zero에 B, V, 1 포함
11 0000 1 0000 00000 → 11(짝수개) B00V 1(홀수개) 000V(짝수개) B00V
💡 Bipolar Encoding : Pseudo-ternary encodingBit 1 → 0V
Bit 0 → LOW와 HIGH를 번갈아가며 ⇒ 한 번 0이 LOW였으면 그 다음 0은 HIGH
-
2B1Q (2개의 Bit가 하나의 signal 요소로 인코딩)
→ 2bits, 4 signal levles(Q)
→ 더 낮은 bandwidth 요구
→ DSL 에서 사용 -
8B6T (8개의 Bit를 6개의 3단계 signal 요소로 인코딩)
→ 8 Bits, 6 three-level signal element
→ +의 개수 = -의 개수(근데, +가 하나 많아도됨)
→ +가 하나 더 있는 신호 요소가 2개 이어지면, 두 번째 신호 요소는 반전됨
- 4B/5B : 4 bit data → 5 bit data
→ 0000이 나타나지 않도록
→ first 2 bits는 1을 적어도 하나 포함(11,10,01)
→ last 3 bits는 1을 적어도 하나 포함(000제외)
→ 몇 개의 5bit code 가능 ? 총 가능 개수 (2^5) - 앞에 00인거 제외(2^3) - 뒤에 000인거 제외(2^2) + 앞에 00이고 뒤에 000인거(00000) 하나 더해줌
= 2^5 - 2^3 - 2^2 + 1 = 32-8-4+1 = 21개
→ block coding가능함! 왜냐하면 4B일 때는 총 16개인데, 5B일 때는 총 21개 이고, 4<5이므로 가능함!
PCM
→ 각 샘플의 신호 크기를 찾아 샘플링
Delta Modulation
→ 이전 샘플과의 차이를 찾아 샘플링
→ 더 단순!
1 : increased from last sample
0 : decreased from last sample
