CPU 가산기
- 가산기(adder)
- 덧셈 연산을 수행하는 논리회로. 디지털 회로, 조합회로의 하나
- 산술논리장치뿐만 아니라 주소값, 테이블 색인 등을 더하는 프로세서의 한 부분으로 사용된다.
- 대부분의 가산기는 2진수의 합을 계산한다.
- 2의 보수나 1의 보수를 이용하여 음수를 표현하는 경우 가산기를 가감산기로 사용한다.
반가산기
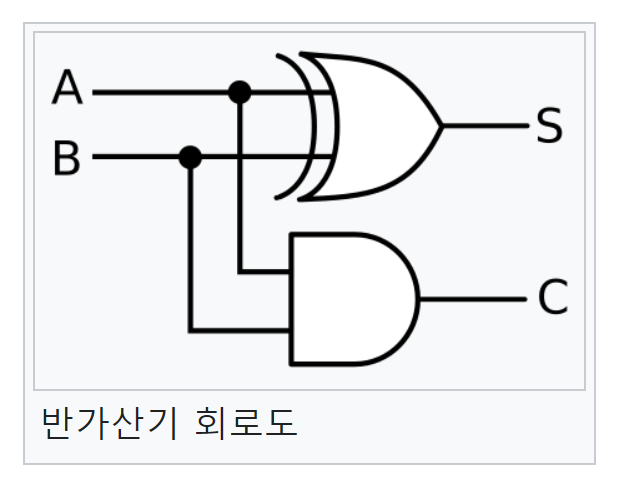
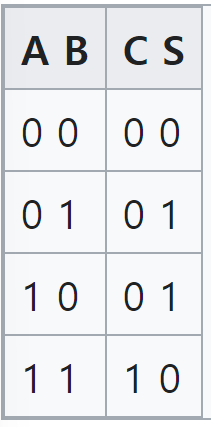
- 반가산기(half adder)
- 이진수의 한 자리수를 연산하고, 자리올림수는 자리올림수 출력(carry out)에 출력한다.
- AND, OR, NOT의 세 종류의 논리회로만으로 구성할 수 있다.
- 입력A, 입력B, 출력S, 자리올림수 출력C의 진리표
전가산기
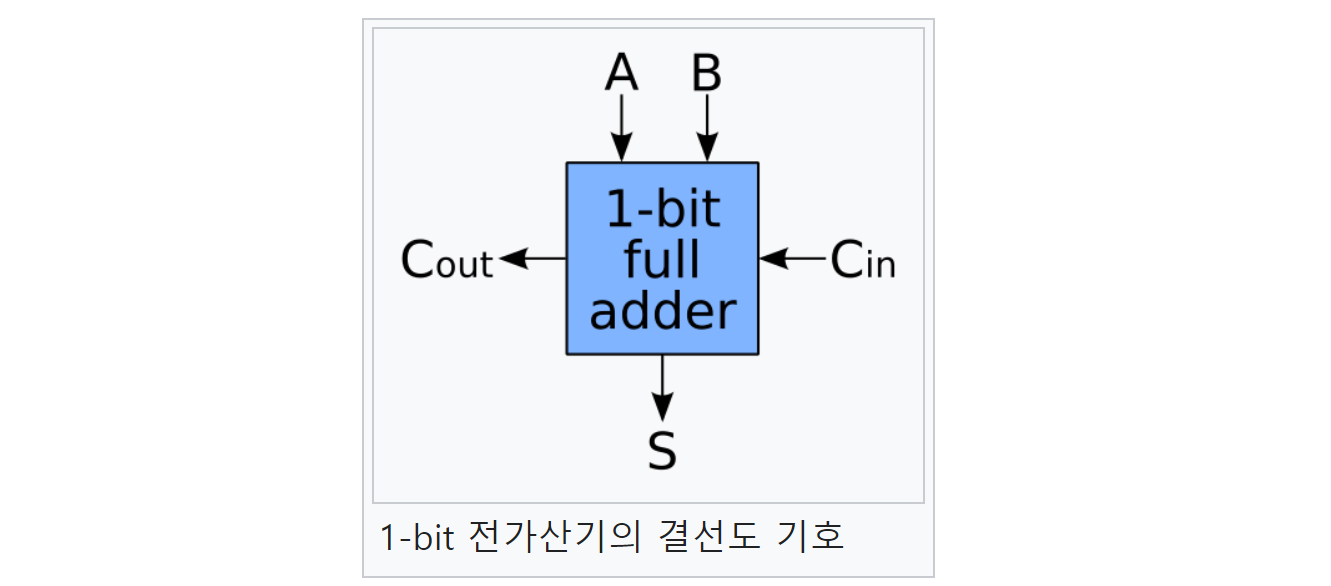
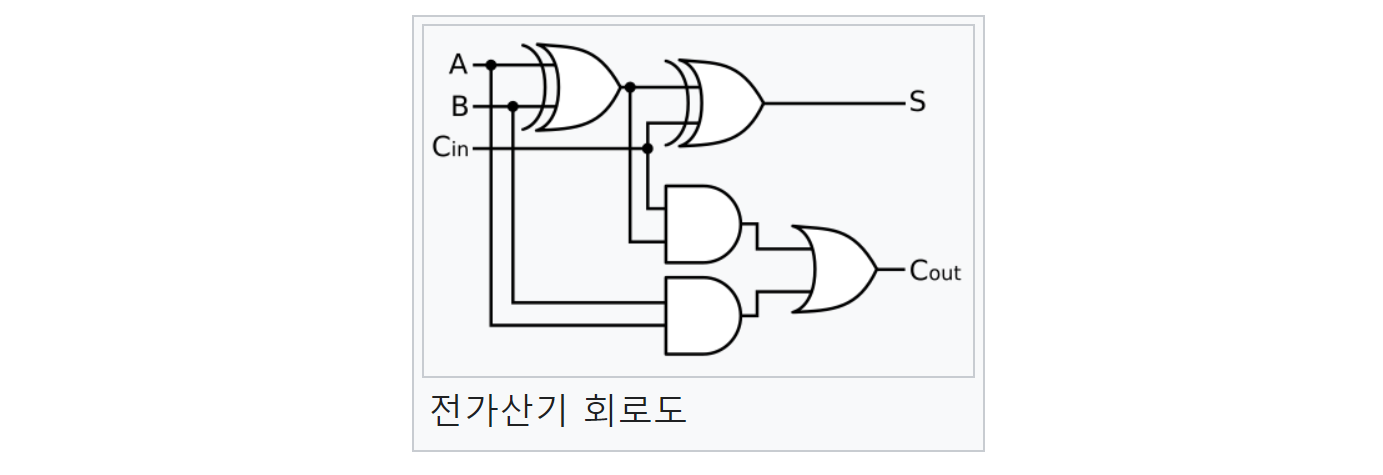
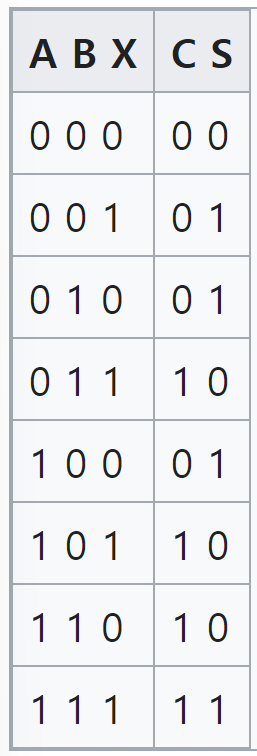
- 전가산기(full adder)
- 이진수의 한 자릿수를 연산하고, 하위의 자리올림수 입력을 포함하여 출력한다
- 하위의 자리올림수 출력을 상위의 자리올림수 입력에 연결함으로써 임의의 자리수의 이진수 덧셈이 가능해진다.
- 하나의 전가산기는 두개의 반가산기와 하나의 OR로 구성된다.
- 입력A, 입력B, 자리올림수 입력 (X=Cin), 출력 (S), 자리올림수 출력 (C=Cout)의 진리표
2진수의 사칙연산
- 정수 산술 연산 (integer arithmetic operation)
- 정수 연산 = 음수 변호나 그리고 사칙연산, 5종 세트
- 음수화 (negation)
- 양의 2진수를 2의 보수로 변환
- 덧셈
- A와 B 2개의 2진수를 더해 C 값을 출력
- 뺄셈
- A에서 B(2의 보수)를 더한 값 C를 출력
- 컴퓨터는 2의 보수를 활용해 뺄셈도 덧셈으로 한다.
- 곱셈
- A와 B 2개의 2진수를 곱해 C 값을 출력
- 나눗셈
- A를 B로 나누고 몫(quotient)과 나머지(remainder)를 출력
보수 (Complementary Number)
- 2의 보수 표기법 (2's complement representation)
- 컴퓨터에서 음수(minus number)를 표현하는 방법은 '부호의 절대값', '1의 보수', '2의 보수' 등이 있다.
- 2의 보수를 사용하면, 계산이 편리하기 때문에 일반적으로 '2의 보수'를 이용해 음수(minus number)를 표현한다.
- '1의 보수'와 '2의 보수' 생성
- '1의 보수'는 2진수로 표현된 양수의 0은 1로, 1은 0으로 치환해 생성한다.
- '2의 보수'는 1의 보수에 1을 더해 생성한다.
- '1의 보수'는 2진수로 표현된 양수의 0은 1로, 1은 0으로 치환해 생성한다.
2진수의 음수화
양수 값을 2의 보수로 변환

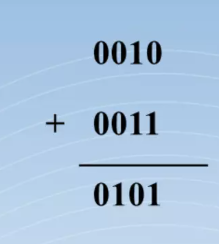
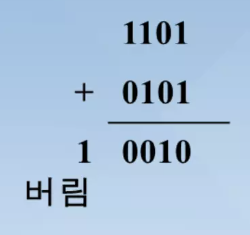
2진수의 덧셈
- 양수와 양수의 덧셈: 2 + 3 = 5
- 음수와 양수의 덧셈: (-3) + 5 = 2
- 자리 올림수가 발생
- 자리 올림수가 발생
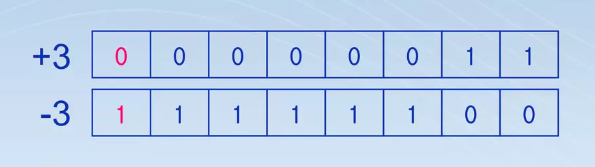
- 음수와 양수의 덧셈: (-6) + 3 = -3
- 자리 올림수가 발생하지 않음
- 자리 올림수가 발생하지 않음
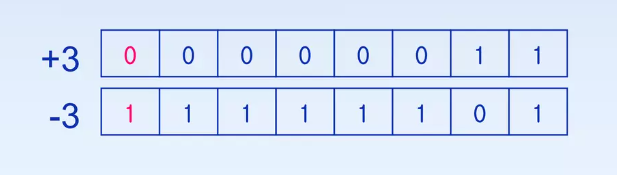
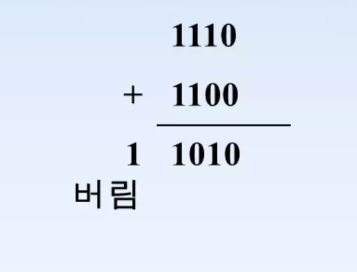
- 음수와 음수의 덧셈: -2 + (-4) = -6
- 자리 올림수가 발생
- 자리 올림수가 발생
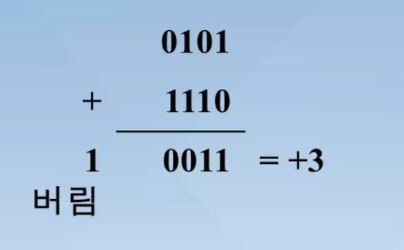
2진수의 뺄셈
- 자리 올림수가 발생하지 않는 경우
- 2 - 5 = +2 + (-5) = -3
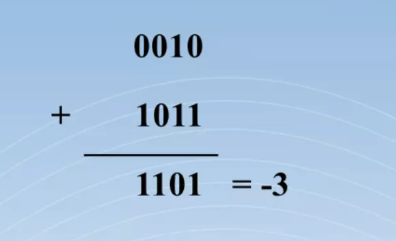
- 자리 올림수가 발생하는 경우
- 5 - 2 = 5 + (-2) = 3
- 5 - 2 = 5 + (-2) = 3
2진수 곱셈
- A * B = C
- 곱하는 수(B)를 승수(multiplier), 곱하여지는 수(A)를 피승수(multiplicand)라고 함
- 4비트의 두 수를 곱하면, 2배인 8비트 길이의 결과를 출력한다.

2진수 나눗셈
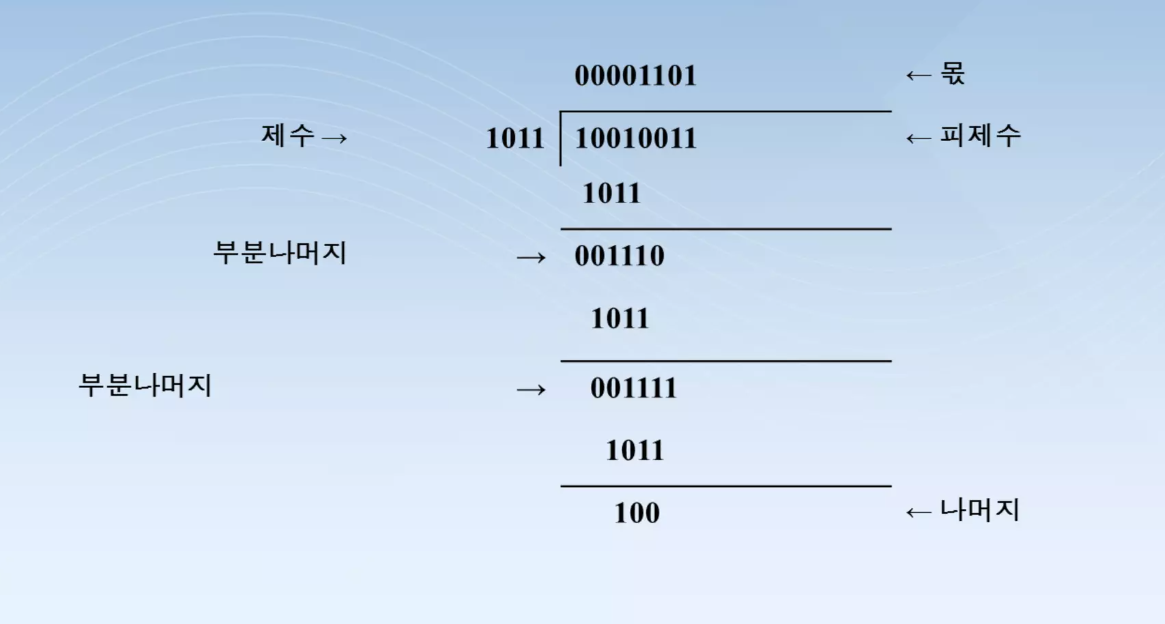
- D / V = Q ... R
- 나누어지는 수 D를 피제수(dividend), 나누는 수 V를 제수(divisor)
- 나눗셈의 결과 몫(quotient) Q와, 나머지 수(remainder) R
2진수와 10진수 변환
- 십진법 (decimal system)
- 0 ~ 9의 10가지의 기호를 이용하여 수를 표현
- 10의 제곱(10^n)으로 자릿수(n)의 값을 계산
- (724)10 = 7 10^2 + 2 10^2 + 4 * 10^0
- 이진법 (binary system)
- 0과 1만을 가지고 수를 표현
- 2의 제곱(2^n)으로 자릿수(n)의 값을 계산
- (101101)2 = 1 2^5 + 0 2^4 + 1 2^3 + 1 2^2 + 0 2^1 + 1 2^0 = (45)10
- 십진수를 이진수로의 변환
- 연속적으로 2로 나눗셈을 수행하면서 얻어지는 나머지에 의해서 만들어진다.
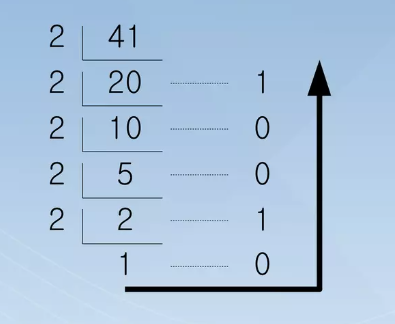
- (41)10을 이진수로 변환
- 41을 2로 연속해서 나눗셈
- 생성된 나머지를 역순으로 정렬
- (41)10 = (101001)2
- 이진수를 십진수로의 변환
- 이진수의 '각 자릿수(n) + 2^n'의 계산 결과를 합산
- (101001)2 = 1 2^5 + 1 2^3 + 1 * 2^0 = 32 + 8 + 1 = (41)10
2진수와 16진수 변환
이진법을 이용해 0과 1만으로 모든 숫자를 표현할 수 있다. 하지만 이진법은 0과 1만으로 모든 숫자를 표현하다보니 숫자의 길이가 너무 길어진다는 단점이 있다. 그래서 데이터를 표현할 때 이진법 이외에 십육진법도 자주 사용한다.
십육진법이 사용되는 주된 이유중 하나는, 이진수로의 변환이 쉽기 때문이다.
- 16진수 기수법
- 디지트(digit)가 0,1,2,3,4,5,6,7,8,9,a,b,c,d,e,f로 구성, 총 16개의 숫자와 알파벳으로 표기한다.
- 디지트(digit)가 0,1,2,3,4,5,6,7,8,9,a,b,c,d,e,f로 구성, 총 16개의 숫자와 알파벳으로 표기한다.
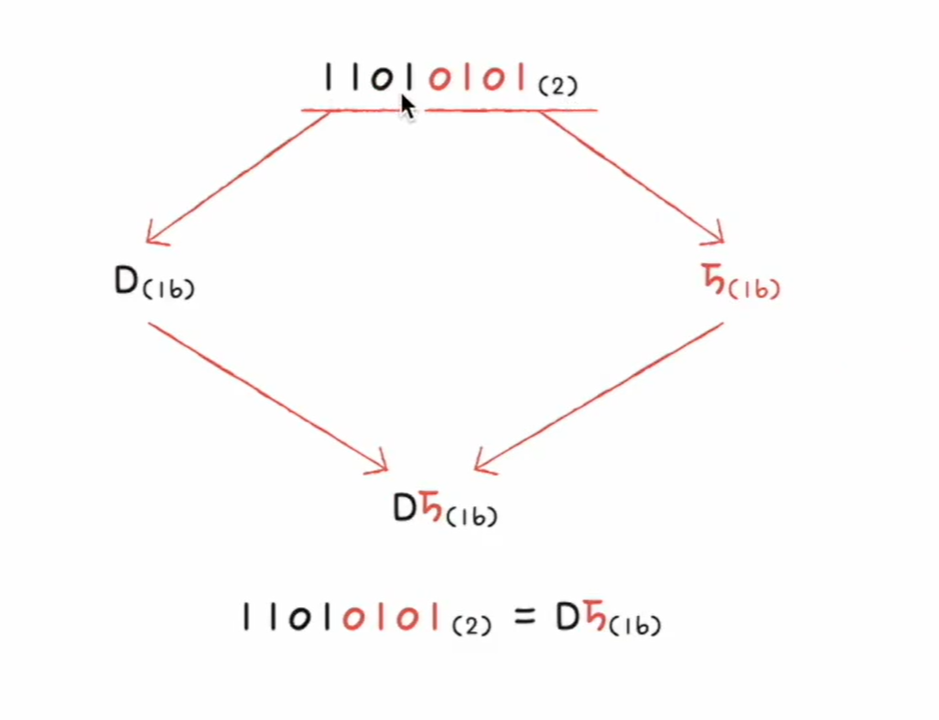
- 십육진수 -> 이진수
- 십육진수 한 글자를 4비트의 이진수로 간수한다.
- 즉, 십육진수를 이루고 있는 각 글자를 따로따로 (4개의 숫자로 구성된) 이진수로 변환하고, 그것들을 그대로 이어붙이면 이진수로 변환된다.
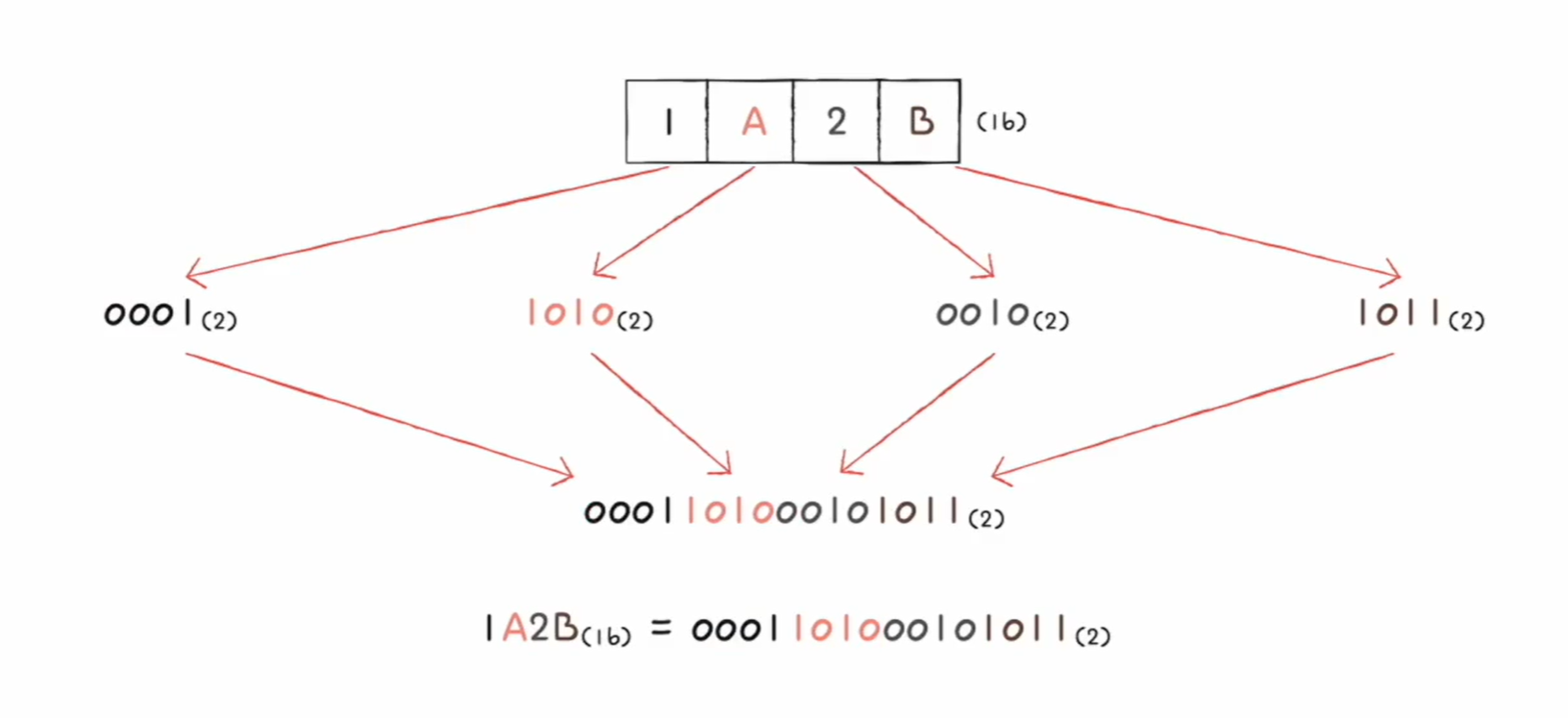
- 십육진수 한 글자를 4비트의 이진수로 간수한다.
- 이진수 -> 십육진수
- 이진수 숫자를 네 개씩 끊고, 끊어 준 네 개의 숫자를 하나의 십육진수로 변환한 뒤, 그대로 이어붙인다.
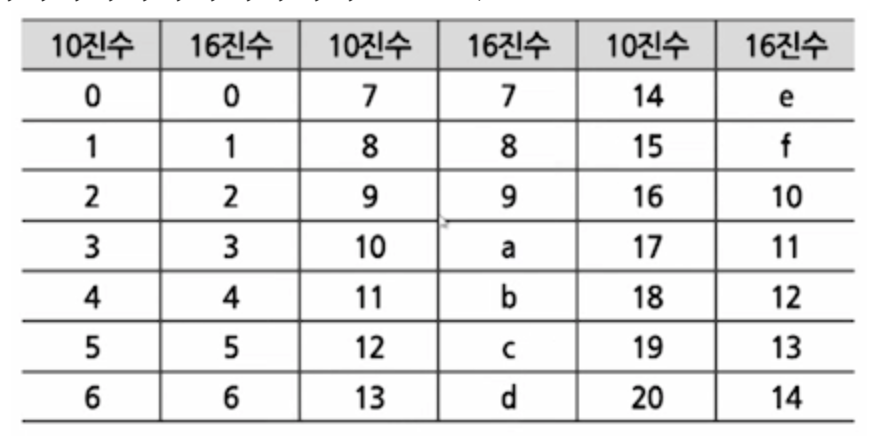
10진수와 16진수 변환
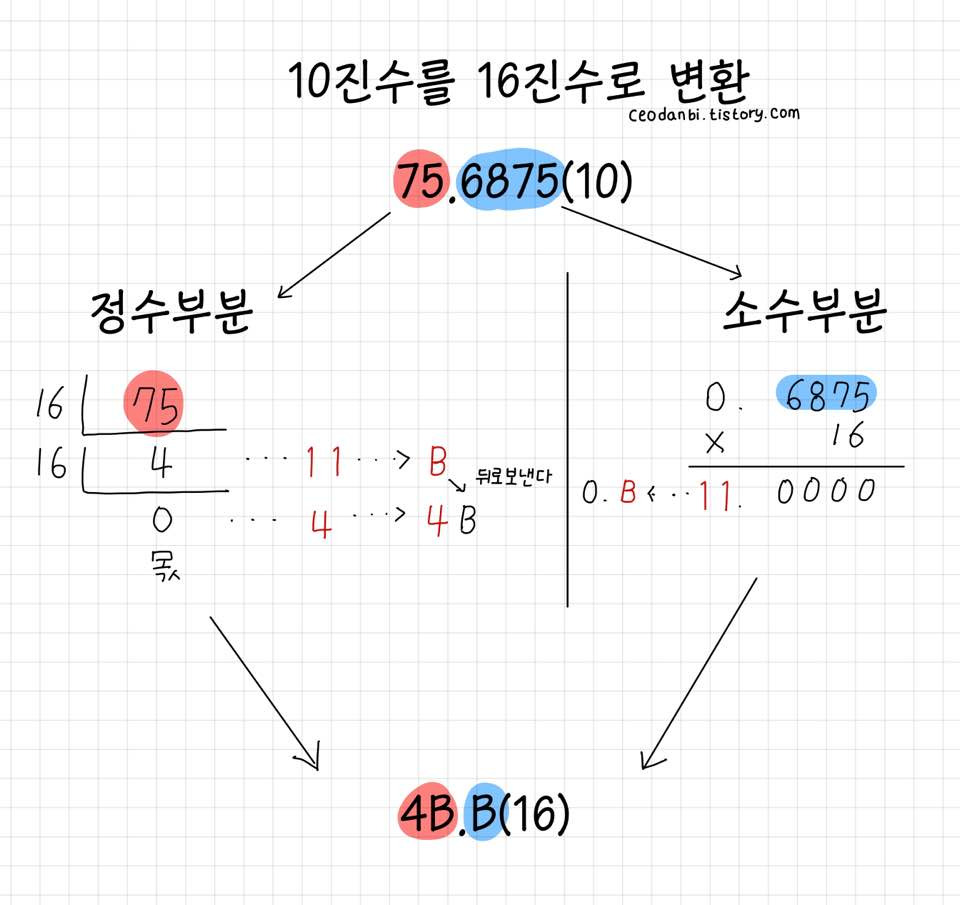
- 10진수를 16진수로 변환
- 정수부분은 16으로 나누고, 소수부분은 16으로 곱한다.
- 그 후 10~15사이의 숫자를 표를 참고하여 알파벳으로 치환해준다.
- ex) 75.6875(10) = 4B.B(16)
- 16진수를 10진수로 변환
- 각 자리 숫자에 16의 거듭제곱을 곱한다.
- 곱한 값들을 모두 더해준다.
- ex) ABC(16)을 10진수로 변환
- C * 16^0 = 12 * 1 = 12
- B * 16^1 = 11 * 16 = 176
- A * 16^2 = 10 * 256 = 2560
- 12 + 176 + 2560 = 2748(10)
- 위키백과: 가산기
- [디지털공학개론] 10진수를 16진수로 변환 - 개발 일지 - 티스토리
- 개발자를 위한 컴퓨터공학 1: 혼자 공부하는 컴퓨터구조 + 운영체제
- 혼자 공부하는 컴퓨터구조 + 운영체제: 한빛미디어 강민철 지음
- 프로그래머가 알아야 하는 2진수 기반의 컴퓨터 동작 원리