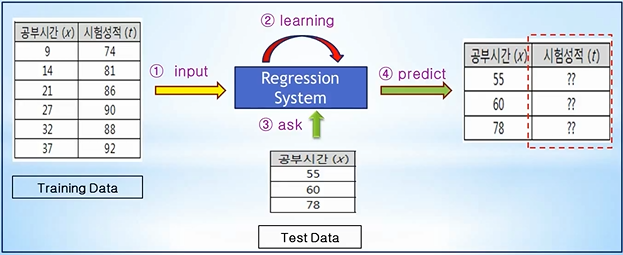
회귀 (Regression)
Training Data를 이용하여 데이터의 특성과 상관관계 등을 파악하고, 그 결과를 바탕으로 Training Data에 없는 미지의 데이터가 주어졌을 경우에, 그 결과를 연속적인 (숫자) 값으로 예측하는 것
ex) 공부시간과 시험성적 관계, 집 평수와 집 가격 관계 등
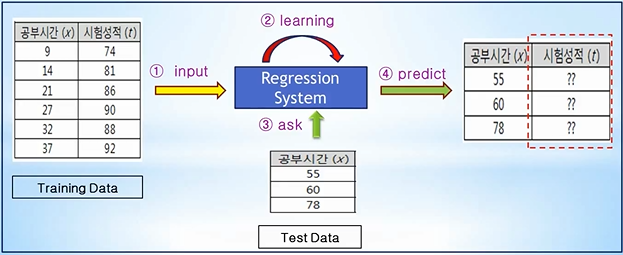
아직 고려할 수준이 아닐지 모르겠지만, 인풋에 대한 결과 값으로 Training을 시키는 만큼 인풋과 결과 값의 상관 관계가 있는 데이터를 사용하는 것도 중요할 것이라고 예측됩니다.
학습 개념
[Step 1] Analyze Training Data

- 학습 데이터(Training Data)는 입력(x)인 공부시간에 비례해서 출력(y)인 시험성적도 증가하는 경향이 있음
- 즉, 입력(x)과 출력(y)은 y = Wx + b 형태로 나타낼 수 있음
[Step 2] Find W and b
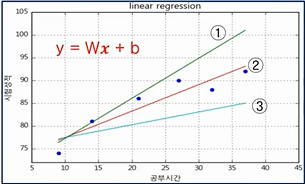
- [Step 1]에서 y =Wx + b 라고 나타낼 수 있기 때문에 해당 하는 여러 직선 中
- Training Data의 특성을 가장 잘 나타내는 가중치 W(기울기), 바이어스 b(y 절편)를 찾는 것이 학습 개념
Training Data의 입력과 출력 간의 상관 관계를 이해하여 어떤 그래프를 나타낼지 예측하는 과정이 꽤나 중요한 과정이라고 생각됩니다.

Training Data의 정답(t) 값과 직선 y = Wx + b 값의 차이인 오차(error) 값을 통하여 가중치와 바이어스를 설정합니다.
오차 (error) = t - y = t - (Wx + b)
오차가 크다면 가중치와 바이어스 값이 잘못된 것이고, 오차가 작다면 가중치와 바이어스 값이 잘 설정된 것이기 때문에 미래 값 예측도 정확할 수 있다고 예상이 가능합니다.
- > 모든 데이터의 오차의 합이 최소가 되는, 미래 값을 잘 예측 가능한 기울기 W와 바이어스 b 를 찾아야 합니다.
손실함수 (Loss Function)
손실함수는 Trainnig Data의 정답(t)과 입력(x)에 대한 대한 계산 값 y의 차이를 모두 더해 수식으로 나타낸 것 입니다.
※ 각각의 오차는 (+), (-) 값이 존재하므로 오차 제곱의 합을 통해 계산합니다.
(제곱을 하기 때문에 정답과 계산값의 차이가 크다면 오차는 더 크기 때문에 학습에 있어 장점을 가집니다.)
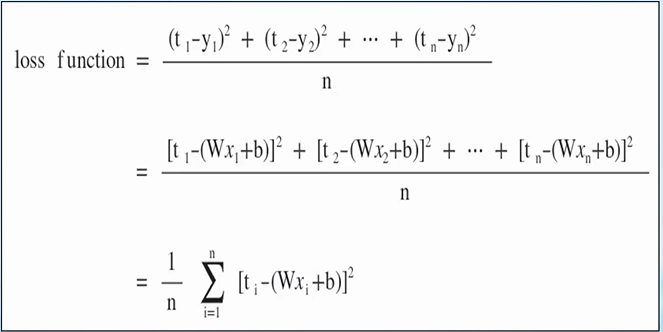
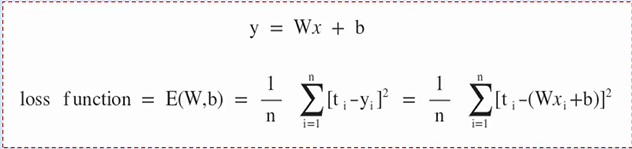
x와 t는 Training에서 주어지는 값이므로 손실함수 E(W,b)는 W와 b에 영향을 받는 함수이며, E(W, b)가 작다는 것은 평균 오차가 작다는 의미입니다.
=> 손실 함수 E(W, b)가 최소값을 갖도록 가중치와 바이어스를 구하는 것이 Regression model의 최종 목적
위 수식에서 손실 함수가 MSE^2 형태인 2차 함수 형태를 띄고 있기 때문에 포물선의 형태를 띄고 있을 겁니다.
(실제로 완전한 포물선 형태를 띄고있을거라 생각되지 않아 설명드릴 경사하강법은 아주 간단한 예측법이라고 생각됩니다.)
- 경사하강법 (Gradient Decent Algorithm)

- 임의의 가중치 W 선택합니다.
- 해당 W에서의 dE(W)/dW 편미분 값을 구합니다.
- if) dE(W)/dW > 0 : W를 왼쪽으로 이동시켜(감소), 손실함수 E(W) 최소값을 찾습니다. elif) dE(W)/dW < 0 : W를 오른쪽으로 이동시켜(증가) 손실함수 E(W) 최소값을 찾습니다.
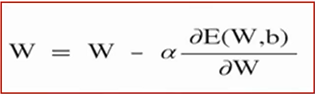
α는 학습율이라고 부르며, W 값의 감소 또는 증가 비율을 나타냅니다.

이처럼 가중치 W와 바이어스 b를 편미분을 이용하여 손실함수의 최소값을 찾는 방법을 경사하강법이라고 합니다.
출처 : 유튜브 NeoWizard 채널 머신러닝/딥러닝 강의
