torch.autograd를 사용한 자동 미분

• 신경망을 학습할 때 가장 자주 사용되는 알고리즘은 역전파 입니다.

• 이 알고리즘에서, 매개변수 (모델가중치)는 주어진 매개변수에 대한 손실 함수의 변화도(gradient)에 따라 조정됩니다.
  -역전파: 먼저 계산 결과와 정답의 오차를 구해 이 오차에 관여하는 값들의 가중치를 수정하여 오차가 적어지는 방향으로 일정 횟수를 반복해 수정하는 방법
  -가중치: 처음 들어오는 데이터에서 다음 노드로 넘어갈 때 모두 같은 값이면 계속 같은 값이 나올 수 밖에 없다. 각기 다르게 곱해야 한다는 것이 바로 가중치 입니다. 값을 변화시켜주는 것 입니다.

• 이러한 변화도를 계산하기위해 Pytorch는 torch.autograd라고 불리는 자동 미분 엔진이 내장되어 있습니다
  - 이는 모든 계산 그래프에 대한 변화도의 자동 계산을 지원합니다.

• 입력 x, 매개변수 w 와 b, 그리고 일부 손실 함수가 있는 가장 간단한 단일 계층 신경망을 가정하겠습니다.

• 코드

import torch

x = torch.ones(5)  # input tensor
y = torch.zeros(3)  # expected output
w = torch.randn(5, 3, requires_grad=True)

b = torch.randn(3, requires_grad=True)
z = torch.matmul(x, w)+b
loss = torch.nn.functional.binary_cross_entropy_with_logits(z, y)

• x는 1로 가득찬 size=5의 텐서
• y는 0으로 가득찬 size=3
• w는 가중치로 requires_grad = True 는 자동미분 여부입니다. True면 자동미분을 하는 것을 의미합니다.
• b는 bias 편향입니다
• z에서 matmul의 경우 행렬 곱을 의미합니다.
• loss 변수가 손실함수 값을 도출해냅니다. binary_cross_entropy_with_logits 여기서 binary_cross_entropy가 손실 함수
  -손실 함수 결과 값은 값이 작을 수록 좋습니다.

Tensor,Function과 연산 그래프(Computational graph)

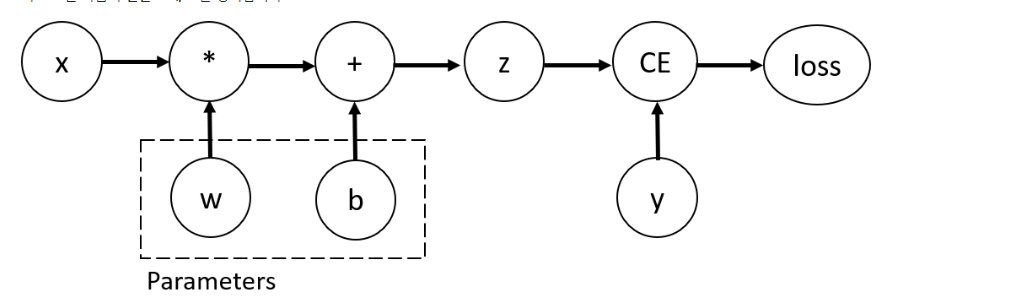
• 이번에 볼 코드는 연산 그래프를 정의합니다.

• 정의되는 연산 그래프
  

• 이 신경망에서 w와 b는 최적화를 해야하는 매개변수 입니다. 따라서 이러한 변수들에 대한 손실 함수의 변화도를 계산할 수 있어야 합니다.
  -이를 위해 해당 텐서에 requires_grad 속성을 설정합니다.
  -그림의 z는 타겟값, CE는 손실 값으로 보면됨

• requires_grad의 값은 텐서를 생성할 때 설정하거나, 나중에 x.requiresgrad(True) 메서드를 사용하여 나중에 설정핧 수도 있음

• 연산 그래프를 구성하기 위해 텐서에 적용하는 함수는 사실 Fuction 클래스의 객체입니다.
  -이 객체는 순전파 방향으로 함수를 계산하는 방법과, 역전파 단께에서 도함수(derivative)를 계산하는 방법을 알고 있습니다.
  -역방향 전파 함수에 대한 참조는 텐서의 grad_fn속성에 저장됩니다.

  • Function에 대한 자세한 정보는 Function 이 문서에서 확인 가능합니다.
  • 도함수는 미분계수를 일반화한 개념으로, 함수의 접선의 기울기를 보여주는 함수이다.

-코드

print(f"Gradient function for z = {z.grad_fn}")
print(f"Gradient function for loss = {loss.grad_fn}")

-결과

변화도(Gradient) 계산하기

• 신경망에서 매개변수의 가중치를 최적화하려면 매개변수에 대한 손실함수의 도함수를 계싼해야 합니다.
  -즉, x 와 y의 일부 고정값에서 가 필요합니다.
• 이러한 도함수를 계산하기 위해 loss.backward를 호출한 다음 w.grad와 b.grad에서 값을 가져옵니다.

-코드

loss.backward()
print(w.grad)
print(b.grad)

-결과

• 연산 그래프의 잎(leaf) 노드들 중 requires_grad 속성이 True로 설정된 노드들의 grad 속성만 구할 수 있습니다.
• 그래프의 다른 모든 노드에서는 변화도가 유요하지 않습니다.
  -성능상의 이유로 주어진 그래프에서의 backward를 사용한 변화도 계산은 한 번만 수행할 수 있습니다.
  -동일한 그래프에 여러번 backward 호출이 필요하면 backward 호출시에 retrain_graph=True를 전달해야 합니다.
  

변화도 추적 멈추기

• requires_grad=True인 모든 텐서들은 연산 기록을 추적하고 변화도 계산을 지원합니다.
• 그러나 모델을 학습한 뒤 입력 데이터를 단순히 적용하기만 하는 경우와 같이 수전파 연산만 필요한 경우에는, 이러한 추적이나 지원이 필요없을 수 있습니다.
  -이러한 경우 연산 코드를 torch.no_grad()로 둘러싸 더이상 연산 추적을 불가능하게 만들어서 False가 나옵니다. 블록으로 둘러싸서 연산 추적을 멈출 수 있습니다.
  

-코드

z = torch.matmul(x, w)+b
print(z.requires_grad)

with torch.no_grad():
 
 - z = torch.matmul(x, w)+b
print(z.requires_grad)

• 첫 번째 줄은 위에서 이미 requires_grad=True로 정의 했기에 True로 나오고
• 두 번째 줄은 torch.no_grad()로 둘러싸 더이상 연산 추적을 불가능하게 만들어서 False가 나옵니다.

-결과

• 동일한 결과를 얻는 다른 방법은 텐서에 detach() 메소드를 사용하는 것 입니다.

-코드

z = torch.matmul(x, w)+b
z_det = z.detach()
print(z_det.requires_grad)

-결과

• 변화도 추적을 멈춰야 하는 이유
  -신경망의 일부 매개변수를 고정된 매개변수로 표시합니다.
  -변화도를 추적하지 않는 텐서의 연산이 더 효율적이기 떄문에, 순전파 단계만 수행할 때 연산 속도가 향상됩니다.

연산 그래프에 대한 추가 정보

• 개념적으로 autograd는 데이터(텐서) 및 실행된 모든 연산들(연산 결과가 새로운 텐서인 경우도 포함하여) 기록을 Function_ 객체로 구성된 DAG(Directed Acyclic Graph:방향성 비순환 그래프)에 저장합니다.
• 이 DAG의 잎(leave)은 입력 텐서이고, root는 결과 텐서입니다. 그래프를 뿌리에서부터 잎까지 추적하면 연쇄 법칙(chain rule)에 따라 변화도를 자동으로 계산할 수 있습니다.

-순전파 단계에서 autograd는 다음 두 가지 작업을 동시에 수행합니다.

• 요청된 연산을 수행하여 결과 텐서를 계산하고
• DAG에 연산의 변화도 기능을 유지합니다.

-역전파 단계는 DAG의 root에서 .backward()가 호출될 때 시작됩니다. autograd는 이때

• 각 .grad_fn 으로부터 변화도를 계산하고
• 각 텐서의 .grad 속성에 계산 결과를 쌓고
• 연쇄 법칙을 사용하여, 모든 잎 텐서들까지 전파합니다.

** Pytorch에서 DAG들은 동적입니다.

• 여기서 주목할 중요한 점은 그래프가 처음부터 다시 생성된다는 것입니다. 매번 backward() 가 호출되고 나면, autograd는 새로운 그래프를 채우기 시작합니다.
• 이러한 점 덕분에 모델에서 흐름제어 구문들을 사용할 수 있게 되는 것 입니다.
• 매번 반복할 때마다 필요하면 모양이나 크기, 연산을 바꿀 수 있습니다.