문제

문제

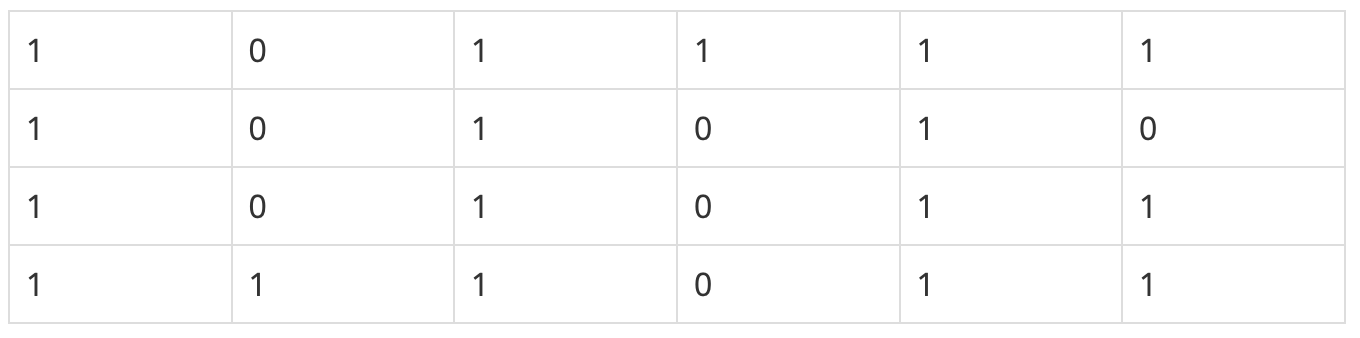
N×M크기의 배열로 표현되는 미로가 있다.

미로에서 1은 이동할 수 있는 칸을 나타내고, 0은 이동할 수 없는 칸을 나타낸다. 이러한 미로가 주어졌을 때, (1, 1)에서 출발하여 (N, M)의 위치로 이동할 때 지나야 하는 최소의 칸 수를 구하는 프로그램을 작성하시오. 한 칸에서 다른 칸으로 이동할 때, 서로 인접한 칸으로만 이동할 수 있다.
위의 예에서는 15칸을 지나야 (N, M)의 위치로 이동할 수 있다. 칸을 셀 때에는 시작 위치와 도착 위치도 포함한다.

입력

첫째 줄에 두 정수 N, M(2 ≤ N, M ≤ 100)이 주어진다. 다음 N개의 줄에는 M개의 정수로 미로가 주어진다. 각각의 수들은 붙어서 입력으로 주어진다.

출력

첫째 줄에 지나야 하는 최소의 칸 수를 출력한다. 항상 도착위치로 이동할 수 있는 경우만 입력으로 주어진다.

풀이

최단 경로를 찾는 문제기 때문에 BFS/DFS를 사용할 수 있다고 판단했다.

이 문제와 같이 2D배열에서 연결된 노드를 찾기 위해서는 상하좌우에 1이 있는 칸이 있는지 확인해야 되니까

dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]

을 사용해서 for i in range(4)로 인접한 칸을 모두 확인하면 된다

그리구 최단경로의 길이를 찾는 문제기 때문에, 2D visited 배열을 0과 1로 단순히 방문여부만 구분하는 것이 아닌, 이 좌표까지 오는데 걸린 경로 길이를 저장하는데 사용한다. 현재 좌표가 (x, y)일 때 for loop에서 인접한 4개의 좌표를 확인하는데, 인접 좌표가 2D배열 내에 유효한 좌표이고, 아직 방문하지 않았으며, 이동할 수 있는 칸 (1)인 경우에 visited 배열에서 그 인접좌표에 현재 좌표의 값 + 1을 저장한다.

현재 좌표가 도착 위치(N-1, M-1)와 일치하면 visited에서 (N-1, M-1)의 값을 반환한다.

코드

def bfs(x, y):
    visited[x][y] = 1
    queue = [(x, y)]
    
    while queue:
        node = queue.pop(0)
        if node[0] == n - 1 and node[1] == m - 1:
            return visited[node[0]][node[1]]  
        for i in range(4):
            nx = node[0] + dx[i]
            ny = node[1] + dy[i]
            
            if 0 <= nx < n and 0 <= ny < m and matrix[nx][ny] == "1" and visited[nx][ny] == 0:
                visited[nx][ny] = visited[node[0]][node[1]] + 1 
                queue.append((nx, ny))

n, m = map(int, input().split())
matrix = [input() for _ in range(n)]
visited = [[0] * m for _ in range(n)]
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]

print(bfs(0, 0))