원본 논문

Introduction

• DB는 query 처리를 가속화하기 위해 정렬된 index에 많이 의지함.
• query의 실행 시간 중 최대 94%가 indexing에 소요되고, DB 메모리 중 최대 55%가 indexing structure을 저장하는데 소요됨 → 빠르고 메모리 사용량이 적은 indexing structure이 중요.
• B-tree, trie, skip list 등의 고전 index structure들은 tree와 같은 계층 형태의 그래프를 이룸 → 기존 구조들은 탐색 과정에서 node를 순차적으로 접근해야 해서 Memory Level Parallelism을 구조적으로 활용하기 힘듦 → Cuckoo Trie에서는 MLP를 활용.
• 기존에 MLP를 활용하는 index가 존재는 하지만 메모리 효율이 좋지 않고 범용성도 별로다. (range scan, concurrency 지원 X, 8byte key만 허용) → Cuckoo Tire는 저 index 대비 메모리 소모량이 3배나 나아짐.
• Cuckoo Trie는 메모리 사용량은 기존 index와 비슷하거나 더 적으면서, query 성능은 벤치마크에 따라 25~360퍼나 나아짐. (osm dataset YCSB-C 경우)

2. Background And Terminology

• Ordered Index point/range query를 빠르게 하는데 도움을 주는 data structure. comparison-based인 B-tree/skip list랑 trie, 혹은 저 둘의 짬뽕이 있다고 한다. 짬뽕은 자세히 안나옴. 전자는 보통 복잡도가 O(logB(N)), 여기서 B는 branch factor 혹은 fanout, N은 data 개수.
  
• Trie 복잡도가 O(L). 여기서 L은 key의 길이. 이 둘 중 누굴 쓰냐는 사실 저 복잡도를 비교해서 정하는 편이다. path compression이라는 최적화가 있다. 하나의 child만을 가지는 node들을 합쳐서 긴 sequence의 node 하나로 취급하는 것.
  
• Bucketized Cuckoo hashing 기본 원리는 cuckoo hashing을 따르는데, 각 hash table에서 최대 보유할 수 있는 개수를 1개가 아니라 여러개로 늘리는 형태의 hashing이다. 기본 cuckoo hashing은 50%정도 차고 난 후에 어느 hash table에도 투입을 못해서 computation이 오래 걸리는 상황이 발생한다. 하지만 위와 같이 바꿀 경우 order을 4로만 해도 삽입시 90%정도까지 찰 때까지 괜찮다는 연구 결과가 있다. 탐색도 order이 4이면 그렇게 안 오래 걸린다. 즉 상수 탐색/삽입이 잘 보장되는 편.
  

3. The need for MLP in index design

3.1 Memory-Level Parllelism

• 현대 processor은 out-of-order execution을 기반으로 의존관계가 없는, 혹은 해결된 instruction 여러개를 동시에 실행하는 것이 가능하다.
• 이를 기반으로 cache miss로 인해 발생하는 latency를 숨기는 것이 가능하다. 진행 중인 memory read들이랑 관련 없는 memory read를 동시에 실행하는 형태로 말이다.
• 이 때 적어도 하나의 resolve중인 cache miss가 있을 때 resolve 중인 평균 cache miss들의 수를 MLP라고 한다.
• MLP 수치는 클수록 좋다. → since more memory access latency is overlapped, thereby shadowing penalty from memory access.

3.2 Index bottlenecks are cause by lack of MLP

• state-of-the-art index design inherently lacks MLP (구조적인 이유) → Can’t access next node before accessing parent node because of hierarchical design.
• Though Cuckoo Trie do MORE memory access, TOTAL cycle spent by lookup is even smaller than state-of-the-art index cycles spent on stalling. (밑의 그림 참고)

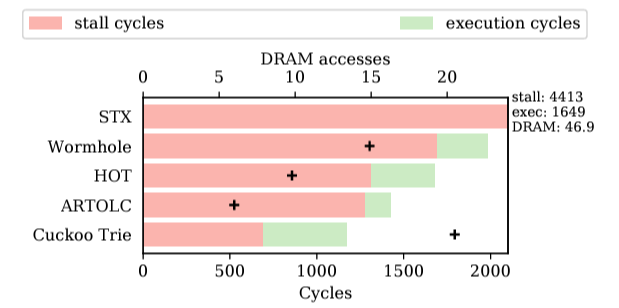
• optimizations trial for state-ofthe-art index structures (SIMD instructions or efficient hash functions) only save execution cycles, while the bottleneck is actually stall cycles.

4. The Cuckoo Trie

• 기존의 path-compressed trie에 bucketized cuckoo hashing을 접목한 index structure.

4.1 Obtaining MLP via a hashed trie representation

• 앞서 말했듯 path-compressed trie의 형태를 기본적으로 가지지만, node들이 explicit하게, pointer을 기반으로 trie를 구성하지 않고 대신 implicit하게, pointer 없이 trie를 구성한다. 이를 이루는데 Bucketized Cuckoo Hash Table이 이용된다.
• 이 자료구조에서의 탐색은 prefetch depth(D)만큼의 prefix에 대응되는 node가 존재할 bucket을 prefetching을 한 다음에 하나가 완료될 때마다 그 다음 prefix에 대응되는 node에 대해서 prefetching을 계속 한다. 최종 leaf를 찾았거나, 존재하지 않는 것을 확인할때까지
  • ‘각’ hash table에서 해당 prefix에 대응되는 node가 존재할 bucket을 prefetching한다. 즉 2개의 bucket을 prefetching한다. 각각은 서로 다른 hasthable을 위한 bucket.
  • 각 bucket은 cacheline 하나에 정확히 대응되도록 설계 (64byte) → prefix당 메모리 접근 2번만 필요.
• 위 방식은 다음의 이유로 MLP를 높이는데 기여한다.
  • 각 prefix에 대응되는 node를 찾는 행위가 서로 의존관계가 없다. 왜냐하면 무슨 prefix에 대해 대응되는 node를 찾아야하는지는 key가 주어지는 시점에서 전부 알 수 있기 때문에 서로의 결과에 의존하지는 않음.
  • 또 BCHT를 사용하기 때문에 hash table을 lookup하는 과정 자체도 서로 다른 key 기반 searching이랑 의존관계가 없음.
  • 이 두가지 이유로 각 prefix에 대응되는 node를 찾는 것에 의존관계가 없어서, parllel하게 진행이 가능.
• 다만 reorder buffer과 miss status holding register(MSHR)에 의해 최대 MLP 수치에 한계가 존재하긴 함.
• D는 MSHR의 개수로 정해짐. (2*D = MSHR 개수. key 하나당 cacheline(bucket) 2개를 접근하기 때문.)

4.2 Hash table with key elimination

• Motive
  • hash table도 결국 key-value structure을 가지고, key에 해당하는 node name은 길이가 길 수 있다.
  • 따라서 direct key storage는 메모리 효율이 별로다. 가변 key도 지원을 효율적으로 못함.
  • 그런데 indirect key는 MLP를 헤친다. 그 key를 읽기 위해 메모리 접근을 한 번 더 해야 하기 때문. 그래서 key를 아예 보관할 필요가 없는 구조를 만든다.
• Method
  • node에서 담당하는 prefix의 마지막 글자와 일부 메타데이터를 통해 구현.
  • 이 metadata랑 prefix의 마지막 글자가 key의 역할을 어떻게 하는지 알려면 먼저 key의 주요 용도가 무엇인지를 이해해야 한다. 이는 다음과 같음
    • node를 다른 table의 bucket으로의 relocate 할 때
    • 특정 node가 우리가 탐색하는 key랑 관련된 node인지 판별할 때

  Relocation

  • metadata 중에는 tag라는 정수가 있다. 이를 기반으로 다른 table에서 특정 key k가 저장되는 bucket을 파악한다.

  • 방식을 알기 전에 먼저 h라고, [0, S*t)의 범위를 가지는 함수가 있다. input은 key. S는 각 table의 bucket 개수, t는 tag 범위를 결정하는 숫자로 논문에서는 16을 사용.

  • h(k)의 결과물을 B(k)랑 T(k)로 나누는데, B(k)는 h(k)/t에 floor 적용 값으로 범위는 [0,S). T(k)는 h(k) mod t로 범위는 [0, t). 여기서 T(k)값을 tag라고 하며, t가 tag 범위를 결정하는 숫자인 이유도 이걸로 알 수 있다.

  • 이후 k라는 key가 두 table에서 어느 bucket에 대응되는지는 다음 공식을 통해 결정된다.

    

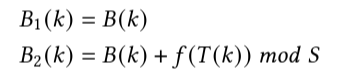
  • 여기서 f는 [0,t)→[0,S)의 범위를 가지는 랜덤 함수이며, mod S는 B(k) + f(T(k))에 대해서 적용한다는 점 참고.

  • 모든 entry는 tag랑 B1(k)인지 B2(k)인지를 표기하는 bit, 이렇게 2가지를 보관을 한다. 그러면 만일 relocation이 필요할 경우, 일단 현재 bucket 값이 어디에 해당되는지 bit로 확인을 한 다음 f(T(k))를 각 경우에 대해 적절히 연산을 해서 다른 위치를 구하면 된다.

  • 그런데 그냥 hash function을 2개 쓰면 되지 않나… 라는 생각이 들었다. 이러면 tag 보관도 필요 없고 그냥 어떤 hash function을 썼는지에 대한 bit만 표기하면 되지 않나…? → jump node 관리가 복잡해짐, 충돌 너무 많이 발생, 탐색에서 full key를 활용하지 않는 구조를 만들려고 함의 복합적 결과.

  Verification of entries

  • prefix에 대한 bucket을 찾은 다음, 그 안의 특정 entry가 실제 그 prefix에 대한 entry인지 확인할 때 활용할 수 있는 특징이 있다. 바로 그 entry의 parent가, 우리가 미리 찾은 parent랑 동일할 것이라는 점.

  • 이를 활용해 다음을 통해 특정 entry와 관련된 key인 k가 prefix p에 대한 entry인지 확인이 가능.

    • k의 마지막 symbol과 p의 마지막 symbol이 동일 → 동일한 parent를 가지는 child가 여러개일 수 있는데, 이 child를 구별하는게 맨 마지막 entry이기 때문에 이 과정이 필수.
    • 해당 entry의 parent가 p[:#p-1]을 통해 찾은 node와 동일 → 앞에 말한 논리 활용

  • 마지막 symbol은 metadata 형태로 저장을 한다. 문제는 동일 parent를 어떻게 판별하냐는 것이다. 여기서 peelable hash function의 특징을 활용한다.

    
    

  • 위는 peelable hash function의 정의 및 Cuckoo Trie에서 사용한 (peelable) hash function과 peeling에 이용되는 함수 Ph의 정의다. 여기서 x*c는 concatenation이며, c가 마지막 symbol,x는 원래 key의 마지막 symbol 제외 prefix 부분이라고 생각하면 된다.

  • 여기에 color이라는 것을 활용하는데 bucket 내의 entry들에 대한 구별에 사용이 된다. B개의 entry를 가지는 bucket에 대해 color의 개수는 2B개가 된다. 이때 사용되는 bit의 개수는 log2(2B)

  • 그러면 relocation 한정 활용되는 metadata는 last_symbol ,color , parent_color 과 앞의 Relocation부분에서 정의한 tag가 활용된다.

  • 이를 활용해서 특정 bucket의 k라는 key를 가지는 entry가 p라는 prefix와 동일한것을 k를 저장하지 않고 판별하는 방법은 다음과 같다.

    • 먼저 마지막 symbol이 같은지를 확인한다. 이는 last_symbol을 활용하면 trivial
    • 이후 동일한 parent를 가지는지 확인한다. 이는 entry의 tag랑 p에서 구한 tag가 동일한지, 그리고 p[:#p-1]에 대응되는 entry의 color이 k entry의 parent_color이랑 동일한지를 확인하면 된다.
    • tag가 동일해야 하는 이유는 현재 entry의 key k의 hash 값, 즉 h(k)가 h(p)랑 동일한지 확인하기 위해서다. 둘의 tag가 동일하다면 h(k)가 B(k)랑 T(k)로 쪼개지는 형, B(k)랑 T(k)를 기반으로 각 table의 bucket을 정하는 형식, 그리고 현재 둘이 같은 bucket에 있다는 점들 때문에 둘이 같은 h값을 가진다는 것이 보장되기 때문. 이 h값이 같아야만 peelable function을 적용한 값도 (앞에서 마지막 symbol이 같다는 것도 확인했으니) 같음, 즉 비교하고 있는 두 녀석의 parent에 대응되는 bucket이 같다는 것을 확인하기 위해 마지막 symbol 비교 및 tag 비교를 하는 것이다. 여기에 parent_color 과 미리 구했을 p[:#p-1]의 color을 비교해야 둘이 같은 entry를 가리킨다는 것을 확인할 수 있다.
      

  • 각 table에 대해 hash function을 2개 쓰지 않는 이유도 이거와 관련된 것으로 추정중. 2개의 독립적인 hash function을 사용하면 parent 확인을 제대로 하기 힘들어서. 왜냐하면 어찌저찌 peelable hash function 특징을 활용해 앞부분 hash value를 확인을 했어도, 이 hash value를 활용해 parent가 table에 저장되지 않았을 수 있기 때문이다. 다른 table에 저장된 경우에 말이다. 그래서 두 table에 대해 공통 hash function을 일단 활용한 다음에 모종의 조작을 통해 2개의 table에 적절히 분배하는 형식을 택한 것으로 보인다. 이 방식이 일으킬 side effect에 대해선 잘 모르겠음.

hash table entry structure

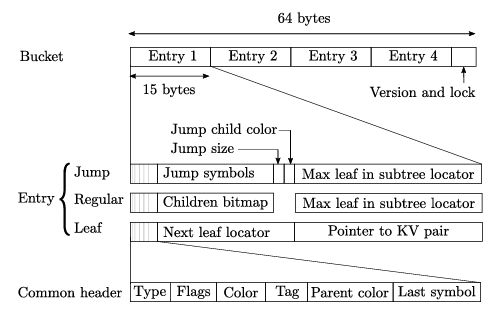
• cacheline이 64byte여서 bucket 하나가 저런 구조를 가진다고 한다.
• 모든 entry에는 common header이 있다.
  • Type : Jump/Regular/Leaf 구별용
  • Flags : Dirty flag.
  • Color : 앞에 말한 entry 구별용 color
  • Tag : T(k)
  • Parent color : parent_color
  • Last symbol : last_symbol
• version, lock은 multithreading 관련이라고 한다. 5에서 다룬다.
• Jump는 path compression과 관련된 내용이라고 한다. 4.3에서 자세히 내용이 나온다.
  • jump size는 현재 jump node가 보유하는 jump symbol들의 총 길이를 의미.
  • jump symbol은 이 node에서 보관하는 연속된 symbol들을 의미.
  • jump child color은
• Regular은 internal node. Children bitmap은 본인이 보유한 children. 또 (Jump랑 같이) 본인 하위 subtree의 max leaf의 locator을 가리킨다. 용도는 후술.
• Leaf는 leaf node. Next leaf locator은 range query에 활용될 다음 leaf 가리키는 locator.
• 위에 나온 locator은 pointer이랑 유사하게, hash table에서의 node 위치를 파악하는데 사용되는 메타데이터로 node의 이름이 x라면 x의 hash value와 node에 대응되는 color의 쌍으로 이루어져있다. 이렇게 locator을 정한 이유는 relocation이 이루어져도 race 문제 없이 찾을 수 있도록 하기 위해서라고…

4.3 Path Compression

• 연속해서 하나의 child만 가지는 node들은 jump node로 압축이 된다.
• 최대 jump node 크기가 정해져있고, 이를 넘어서는 chain이 형성되는 경우 쪼개가지고 각각에 대해 jump node를 만듦.
• jump node에서의 탐색은 depth라는 변수를 활용한다. 이 값은 평소엔 0인데, jump node를 탐색하는 경우에는 추후 설명할 Algorithm2의 FindChild에서 이 값을 기준으로 jump node에서 보관하는 symbol들 sequence를 어디까지 탐색하는데 추적하는데 이용된다.
• jump node의 symbol들을 탐색하는 과정에서 mismatch가 확인되면 대응되는 key가 발견되지 않았음을 의미. 반면 jump node의 symbol들에 대해서 다 통과가 되면 이후 SearchByColor이라는 알고리즘을 통해 다음 child를 구한다. 자세한 과정은 밑의 Algorithm 2 부분 설명 참고.

4.4 Lookups and range iterations

• Lookups

  • Algorithm 1을 기반으로 찾음. 해당 내용 참고.
  • leaf를 찾으면, 일단 그게 진짜 leaf인지 부터 확인하고 맞으면 leaf entry의 KV pair 가리키는 pointer을 기반으로 key가 실제로 대응되는 key인지를 확인. 맞으면 value return. 틀리면 fail.
  • hash table 기반이어도 이런 trie 기반 탐색을 굳이 선택한 이유는 각 hash table의 entry가 전체 key를 저장하지 않도록 하기 위해서다. 메모리 소모량과 indexing speed 사이의 균형을 찾기 위해서. 메모리 소모량을 극단적으로 줄인 경우가 traditional indexing 기반 자료 구조고, indexing speed를 극단적으로 줄인 경우가 통상적인 hash table 구조들…로 추정됨.

• Range (사실 file indexing과 관련이 없…나요? batch I/O에서는 활용할 수도 있지 않을…까요?)

  • k1과 k2사이의 key들에 대한 value 구하기.

  • 그럴려면 먼저 자료 구조 상에 ‘실제로’ 존재하는 시작 key를 알아야 한다. 위의 k1은 그냥 기준용 key이기 때문

    • 먼저 k1이 존재하는지를 trie상에서 찾는다. Algorithm1 활용. 만약 없을 경우, predecessor search 알고리즘을 활용, 이전 node가 right sibling인 predecessor을 찾을 때까지 올라간 다음, 거기의 left sibling으로 이동, 이후 해당 sibling기반 subtree의 maximal leaf로 이동한다.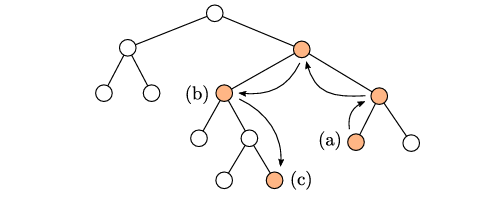

      

      이걸 하는 이유는, 일단 start key가 k1보다 크거나 같은걸 만족하는 애들 중 가장 작은 trie 내 key라는 점에 유의하자. k1이 존재하지 않으면 탐색 ‘도중’에 멈추게 될 확률이 높다. 일단 이 점 때문에 next locator 기반의 linked list로 start key를 찾는것은 안된다.

      그러면 일단 현재 node 기준으로 위에 말한 predecessor search 알고리즘을 기반으로 leaf를 찾아야 한다. 그 다음에 거기서 next leaf locator을 통해 start key를 구해야 한다.

      이 때 위로 올라가는 메모리 접근은 이미 접근한 node들이기 때문에 cache에 관련 정보가 있을거라 탐색이 상대적으로 빠르지만, 이후 left sibling 이동 후 거기 subtree의 maximal leaf로 이동하는 것은 접근한 적이 없기 때문에 메모리 접근이 많을 수록 느리다. 그래서 Jump랑 Regular node는 max leaf in subtree locator을 기반으로 빠르게 탐색할 수 있도록 유도한다.
      

  • 이후 효율적으로 key-value pair을 구할 수 있어야 한다.

    • 이는 leaf node의 next leaf locator을 활용하면 된다.

  • 위의 구조에선 다음 key의 value를 미리 구하는 것이 불가능하다. 현재 node의 내용물을 읽어야 다음 읽어야 할 내용물이 있는 node 파악이 가능하기 때문. 그러면 MLP를 활용하지 못한다고 볼 수 있다.

    흔히 이를 해결하기 위해 각 leaf가 여러개의 key를 가질 수 있도록 유도하도록 prefix를 truncate하는 것이라고 하나, 이러면 insertion이 복잡해진다고 한다. 왜냐하면 leaf가 여러개의 key를 가지는 것이 range query에서 실제로 의미가 있도록 key들을 이동시켜가지고 leaf당 key 개수가 균형이 잘 맞춰지도록 유도해야 해서 그렇다고…

    그래서 여기서는 이를 구현 안함. 대신, leaf node를 구하면 그것에 대해 작업을 하고 그 다음 leaf에 대한 내용물을 또 찾는 것이 일반적으로 흔하다는 것에 착안해서 leaf를 반환할 때마다 그 leaf에 있는 next locator과 대응되는 leaf를 prefetching한다고 한다. DB에서의 작업이 memory latency보다 보통 길기 때문에 효과적이라고 한다.
    

4.5 Insertion and deletions

• Insertions
  • 일단 들어갈 후보 node를 찾아가는 것은 Algorithm 1과 동일하다. 해당 key가 존재를 안하니 결국 언젠가는 막힐텐데, 여기서 3가지 경우로 나뉜다.
    • 멈춘 곳이 regular node이면 그냥 새로운 leaf가 추가된다. children bitmap만 갱신
    • 멈춘 곳이 leaf node인 경우 해당 node가 가리키는 key와 삽입하는 key와 비교후, 공통 prefix가 결정이 된다. 이 공통 prefix를 기반으로 하는 regular/jump node가 기존 leaf node를 대체한다. 그 node에는 두개의 leaf가 추가되는데, 하나는 기존에 있던 key에 대응되는 leaf, 다른 하나는 새로 삽입하는 key에 대응되는 leaf.
      
    • 멈춘 곳이 jump node인 경우, 일단 거기랑 겹치는 부분은 또 얼마나 되는지를 확인한 다음에 그 부분을 기반으로 regular/jump node를 만든다. 이후 regular node 삽입처럼 새로 만들어진 node의 children bitmap만 갱신.
  • 정확히 어떤 bucket의 어떤 entry에 들어가는지는 앞에서 소개한 hashing function 기반으로 cuckoo hashing처럼 정해지니 생략.
  • 이렇게 node가 만들어지고 hash table에도 저장이 되면 trie상에서도 몇가지 갱신이 필요하다.
    • 먼저 leaf들 간의 linked list를 갱신할 필요가 있다. 이 때 현재 leaf의 predecessor을 찾는 과정이 필요한데 앞에서 소개한 predecessor search랑 똑같이 해서 찾는다.
    • 그리고 현재 leaf가 하나 이상의 subtree에 대해 maximal이라면 대응되는 subtree root의 subtree-max locator도 업데이트가 되어야 한다. 이는 위로 올라가면서 갱신이 안될때까지 갱신하면 되지 않나 싶다. (코드를 봐야 할듯)
• Deletions
  • 먼저 삭제할 key가 있는 leaf를 Algorithm 1을 기반으로 찾는다.
  • 이후 bitmap에서 해당 leaf가 삭제되었다고 갱신, linked list에서도 제거. (predecessor을 찾아야한다.)
  • 만약 이 제거로 특정 subtree가 하나의 leaf만을 가지게 되었다면 그 subtree 전체가 하나 남은 leaf로 대체가 된다.
  • 또 subtree-max pointer들도 적절히 갱신, 그리고 해당 leaf를 hash table에서도 삭제를 해야 함.

4.6 Design rationale

• 이 자료구조의 디자인 목표는 index speed와 메모리 효율의 균형
• Unique key prefixes
  • point operation 속도를 hash table 기반 자료구조에서 높이는 방법은 full key를 storing하는 것이지만, index structure이 그만큼 비대해져 메모리 효율이 좋지 않기 때문에 그러지 않고, prefix를 저장하는 형태를 택함
• Symbol Size
  • key의 한 character, 그러니까 symbol의 크기도 이 논의와 관련이 있다.
  • 4.1에 나온 내용에 따르면 parallel memory access는 최대 D까지만 가능. 그러면 trie의 level이 L인 경우, L/D만큼의 DRAM round trip이 불가피.
  • 즉 L을 최대한 줄여야 이득이다. 이는 symbol size를 늘리면 해결이 된다. symbol의 ‘길이’를 줄이는데 도움이 되기 때문. 문제는 그러면 internal node의 child bitmap의 크기가 늘어나게 된다. child bitmap의 크기가 symbol size랑 동일해야 하기 때문. 그러면 cache line bucket당 들어갈 수 있는 entry가 줄어들 수 있고, 결국 bucketing이 효율적이지 못하게 되는 문제가 생길 수 있다.
  • 논문서 사용한 symbol size가 얼마인진 모르겠다. 코드 확인이 필요할듯.

4.7 Limitations

• Path Compression only saves space, not DRAM acceses
  • jump node에 포함되는 prefix도 미리 prefetching을 시도하기에 jump node가 있어도 실질적으로 DRAM 접근 횟수가 줄어들지 않는다.
  • 기존 index structure은 jump node가 있으면 실제로 DRAM 접근 횟수가 줄어든다는 점과 차이를 가짐.
  • 그럼 jump node, 즉 path compression이 cuckoo trie에서 가지는 의의는? index structure이 차지하는 메모리 양이 많이 줄어듦.
• Keys with long common prefixes
  • 위의 이유와 연계된 부분. jump node가 기존 index structure과 다르게 DRAM 접근 횟수를 줄이는 것이 아니다보니, 아주 긴 공통 prefix를 가지는 경우에 대해서는 비효율적일 수 있다. 관련 내용은 6.2에 있다고 함.
• Superfluous memory acceses
  • 의미없는 memory access가 발생할 수도 있다.
    • 특정 prefix에서 이미 leaf를 찾았는데 그 이후의 prefix에 대해 이미 메모리 접근을 시도하고 있는 경우.
    • 매 접근마다 양측 table에 해당 node가 있을 bucket을 fetch하지만 실제로는 둘 중 하나의 bucket에만 존재하니 매번 한번의 memory access를 과하게 한다고 볼 수 있다. (Cuckoo hashing의 근본적 한계)
    • jump node로 compress된 영역에 대응되는 prefix에 대한 memory access 예약도 의미없는 예약이다. 다 통합해서 한번만 접근해도 괜찮기 때문.
  • 다만 하드웨어가 이미 저 정도의 superfluous memory access 감당이 가능해서 괜찮다고 한다. 6.6에서 다룬다고 함.

5. Concurrency support

• linearizable insert, delete, lookup, predecessor/successor search를 지원. 이 때문에 range는 atomic하지 않는데, predecessor/successor만 linearizable하고 range는 이를 여러개 포함하기 때문…이지만 file indexing에서는 별 상관없어 보인다.
• optimistic lock 기반.
  • search는 변조를 안하기에 lock을 아예 acquire 안함
  • write는 영향받는 bucket 관련 lock만 취득. (Bucket cacheline에 있는 lock) 이 bucket을 찾는 과정은 변조가 없기에 lock acquire을 안함.
  • search는 bucket별로 있는 version을 기반으로 race condition 판별. Writer은 write 후 이 version을 매번 update.
  • update마다 version은 2회 increment. update 전에 한번, 그리고 업데이트 후에 한번.
  • read는 version이 홀수거나, 본인의 값이랑 다르면 문제가 있다고 판별이 가능. bucket내의 entry를 읽을 때 확인하며 정확히는 Algorithm 2의 EntriesFor에서 이루어지나 pseudocode에서는 생략했따고 한다.
• Updates
  • 본인이 insert/delete과정에서 update해야 하는 모든 내용물과 관련된 bucket들을 먼저 4에서 설명한 알고리즘들을 기반으로 찾는다.
  • 이후 이 bucket들의 lock을 취득. 과정에서 동시에 atomic하게 얻는건 불가능하기에 취득 후 version이 초기랑 같은지를 compare-and-swap atomic operation을 통해 확인한다.
    • insertion의 경우 parent, insert 되는 node의 predecessor, subtree-max 영향 node 관련 bucket들을 lock
    • deletion의 경우 parent, delete 되는 node의 predecessor, subtree-max 영향 node, delete되는 node 관련 bucket들을 lock
  • lock 취득이 완료되면 write, 이후 전부 free.
  • 새로운 leaf는 생성시 lock된 상태, 작업 완료 후에 free.
  • update 순서는 4.5의 순서랑 동일.
    • 이 순서를 따르면 대부분 consistent한 value를 가지지만 subtree-max나 next 관련 locator의 경우에는 inconsistent한 value를 가질 수 있다. node가 삭제/추가 되었는데 아직 저 locator을 업데이트 하지 않은 경우가 해당. → lock을 한번에 취득하긴 하나, write를 본격적으로 하기 전의 version update를 하지 않았을 때 해당 bucket을 scan할 경우 이 상황이 발생할 수 있다. 이를 해결하기 위해 insert의 경우 stale subtree-max나 next를 가리키는 leaf에는 dirty flag를 표기. 그리고 scan이 dirty leaf를 읽은 경우 operation을 다시 시작한다. locator update가 완료되면 dirty를 해제한다. deletion의 경우 저 flag를 삭제됨 표기를 하는데 사용된다. 이러면 삭제된 leaf는 아예 탐색을 하지 않도록 유도하는 것이 가능하고 이를 가리키는 subtree-max pointer도 한번에 무효화하는 것이 가능.
      
• Key Searches
  • 현재 읽고 있는 node의 relocation 여부만 잘 판단할 수 있으면 문제가 없다.
  • 이 문제가 없도록, 두 가능한 bucket을 읽은 다음에 그것의 parent의 version number을 확인, 달라졌을 경우 다시 시도하는 형태를 가진다. Algorithm2의 FindChild부분이 이 부분을 나타냄.
    • 만일 version이 달라진 후 relocate가 된거면 그냥 재시작을 통해 다시 찾을 수 있다.
    • 삭제의 경우도 version을 바꾸는게 가능하다. bitmap을 조작하기 때문. 이것도 재시작을 한 다음에 없다라는 결론을 내리게 될거다.
• Predecessor searches
  • update랑 range scan이 수행하는 search. 이것도 concurrency에 영향을 받는다.
  • node의 predecessor을 찾은 후에 탐색했떤 모든 bucket들의 version number이 달라지지 않았음을 확인해야 한다.
• Range iteration
  • range에서 predecessor search가 문제없이 완료된 후 k1이라는 key 내용물도 읽고 다음 key를 next locator로 파악하려고 한다 해보자. 이 때 locator이 갑자기 internal node가 되었거나 삭제되었을 수 있다.
  • 그래서 읽기 전에 k1을 다시 읽어서 같은 version인지 확인하는 형태로 검증을 한다.
  • 달라졌을 경우, 해당 k1에 대한 search를 root부터 다시 시작하고 거기서의 next locator을 참고하는 형태로 진행.
• Resizing
  • table의 resize가 필요한 경우, 일단 해당 table이 갱신이 되지 않도록 marking을 한다.
  • 이후 read 관련만 old table에 대해서 작업이 이루어질 수 있도록 하고, 그 사이에 새로운 hash table을 만들어서 내용물 복사를 완료한 다음에 그걸 작업에 활용할 수 있도록 pointer?을 바꾸면 된다.

번외 : 알고리즘 설명

Algorithm 1

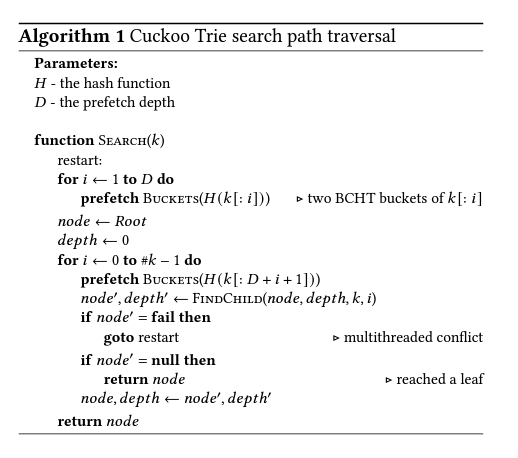
• Search는 특정 key에 대응되는 leaf node를 찾는다.
• 각 prefix 후보 Bucket들을 prefetch후 entry를 탐색, child가 있는지를 확인한다. 없으면 해당 node가 leaf.
• depth는 jump node 탐색 중에 활용이 된다. 자세한건 4.3 및 Algorithm 2 설명 참고.
• 굳이 이렇게 각 prefix에 대해서 prefetching을 한 다음에 일일이 trie 형태로 탐색하는 구조를 가진 이유는…
  • 4.4에서도 얘기했듯 index speed와 메모리 소모량 사이의 균형을 찾기 위해서고,
  • path compression 때문에 온전한 key에 대한 hash entry를 가진다는 것을 보장하지 못해서인 것으로 보임. (추정)

Algorithm 2

• Findchild가 핵심. i번째 (i=0~#k-1) 까지 포함한 prefix 관련 node에서 i+1번째까지 포함한 prefix 관련 node로 넘어가려고 할 때 활용.
• 일단 현 node가 leaf인지 확인. 본인이 leaf면 이를 알리도록 null을 반환.
• child가 존재가 가능한 경우, 일단 i+1번째까지 포함한 prefix에 대한 hash value를 구한다. 이때 prefix의 마지막 character을 논문에서는 ki로 표기했다… ki+1이 아니라. 헷갈리니 참고.
• child는 regular/jump node에 대해서 존재하는 것이 가능하다.

  • regular node의 경우 현 node에서 마지막이 ki인 leaf가 존재하는지를 children bitmap을 기반으로 판단한다. 없는 node에 대해서 탐색 과정이 이루어지지 않도록 방지하기 위함. 없으면 null을 반환. 이 node가 전체 key랑 관련된 leaf라 볼 수 있기 때문.

    만약 존재하는게 확인되었으면, 4.2 부문을 그대로 수행하는 SearchByParent를 수행, 다음 prefix랑 대응되는 node entry가 위치하는 bucket 및 위치를 구해서 반환한다.
    

  • jump node의 경우는 4.3에서 얘기한 것을 활용한다. else문에 해당. 먼저 depth가 jump node에서 보관하는 symbol의 size보다 아직 작으면 계속해서 이 FidnChild를 갱신된 depth에 대해 호출하도록 유도한다.

    매 호출마다 depth를 기반으로 jump node 보관 symbol sequence의 depth번째 symbol이, ki랑 같은지를 확인. 같지 않으면 바로 null과 초기화된 depth를 반환, 같은 경우라면 아직 탐색이 완료되지 않은 경우 depth를 계속 increment한다.
    

  • 그렇게 increment된 depth가 결국 연속된 호출을 통해 node에서 보관하는 key size와 같아지면 jump node에서의 탐색이 완료되었음을 의미한다. 그러면 SearchByColor이라는 함수를 수행하게 된다.

    사실 SearchByColor의 개념적 역할은 SearchByParent와 다를게 없다. 해당 jump node 하위의 child중 우리의 prefix랑 관련된 node를 찾는 역할이다.

    그럼 왜 별개의 함수를 만들었는가? child랑 현재 key의 parent가 같은지를 확인하려면 위에서 언급했듯 peelable hash function의 특징을 활용해 서로의 parent의 hash value가 같은지가 우선 확인이 필요하기 때문이다. 그 다음에 color 비교도 하고. 문제는 우리는 key를 아예 저장 안하고 마지막 symbol만 저장하며, jump node는 앞에 여러개의 symbol들을 포함하기 때문에 서로의 parent 간의 hash value 비교를 현재 가지고 있는 메타데이터만으로 판별하는 것이 불가능하다. 2개 이상의 끝부분 symbol들이 관여해서 그렇다.

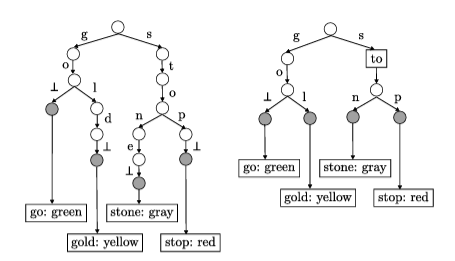
    그러면 어떻게 특정 entry가 우리가 탐색에 사용하는 prefix랑 대응되는 entry임을 파악하는가? 구조적으로 jump node는 child를 1개만 가질 수가 있기 때문에, jump node의 child에 대응되는 color을 jump node에서 보관한다. 이후 entry 비교시에 last_symbol을 비교하는것과 더불어 이 jump child color이 entry의 color과 같은지를 확인하면 판별이 가능하다.

    • Jump node가 child를 1개만 가질 수 있는 원리는 이 그림 참고. 좌측이 jump node 없는 경우, 우측이 jump node 있는 경우.
      

6. Evaluation

• 타 자료구조를 정확히 아는 것이 아니어서 설명이 부정확할 수 있을것 같습니다.

6.1 Expreimental setup

• Platform, setup은 논문 참고
  
• HOT, Wormhole, ARTOLC, STX, MlpIOndex index structure 활용.
  
• Datasets
  • rand-8 : random 8-byte keys
  • rand-16 : random 16-byte keys
  • osm : 64-bit encoding of random OpenStreetMap location
  • az : (item ID, user ID, time) 기반 tuple. Amazon product review
    • 긴 common prefix를 가지는 dataset이라 cuckoo-trie 한정 worst-case.
  • reddit : 2018년까지의 Reddit 사용자 이름 모음.
  • index structure과 key set은 전부 용량이 1GB 이상으로 시스템의 전체 LLC(Last-Level-Cache)보다 용량이 훨씬 크다고 함.
• Workloads (uniform query distribution)

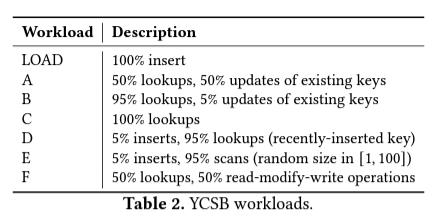
• 이후 그래프는 전부 논문 참고.

6.2 Point operation performance

• Multicore scalability (thread 개수 기반 speedup)
  • rand-8 dataset
  • lookup : YCSB-C, insert : LOAD
  • 두 경우 모두 linear 경향을 보임. Wormhole, ARTOLC는 insert의 경우 saturation을 보임.
• Throughput
  • scalable/unscalable 간의 간극을 줄이기 위해 single-thread execution만 고려해서 논문에서는 설명.
  • 대체로 성능이 더 좋음. 20~360% 성능 차이를 보이는 경우는 YCSB-C + osm 조합.
  • 더 느린 경우는 다음의 이유 때문이라고 한다.
    • long common prefix 때문에 az에서 느리다.
    • ARTOLC가 상대적으로 insertion throughput이 더 좋다. Range query 지원을 위해 trie 이상의 구조를 가지지 않기 때문이라고 한다. (cuckoo trie는 linked list 보유) 대신 메모리 효율이 상대적으로 별로.
    • YCSB-D의 lookup operation의 경우 최근에 삽입한 key들의 lookup을 보통 한다. 이러면 메모리 접근 횟수보다는 수행하는 instruction의 개수가 더 적은 쪽이 유리하다. cache 효과를 많이 볼 수 있기 때문. ARTOLC의 경우 상대적으로 index structure 구조가 덜 복잡해서 이 점에서 우위를 점한다고 한다.

6.3 Scalability to dataset size

• dataset 크기 증가 → tree의 depth 증가 → 느려짐
• 또 tree 크기가 증가 시 cache에 tree 전체가 들어가기 힘들어짐 → DRAM까지의 접근이 더 자주 발생 → 또 느려짐
• 다만 cuckoo trie는 상대적으로 이 느려지는 속도가 덜하다. 여러개의 메모리 위치 접근을 동시에 해 latency를 줄이는 MLP를 적극적으로 활용하기 때문.
• Wormhole의 경우에도 이 영향을 거의 받지 않지만, 기본 속도가 cuckoo trie보다 많이 느리다.
• (개인 의견) section 2에서 언급한 O(L)보다 O(logB(N))이 많이 더 큰 경우도 어느정도 영향을 주지 않을까 싶다. Wormhole도 key의 길이가 성능이랑 연관된 factor이기 때문에 그렇게 생각.

6.4 Range iteration performance

• dataset loading 후 YCSB-E operation을 50M 수행. 연산이 이렇게 많은 이유는 Wormhole의 throughput이 load 직후에 좀 느려서라고 함.
• throughput이 타 자료구조 대비 많이 안좋다. 이는 4.4에서 택한 전략이 잘 먹히지 않기 때문인데, key를 취득 한 후에 이에 대한 작업을 하는데 소요하는 시간이 거의 없기 때문. (value만 취득하고 끝)
  • 이 전략을 잘 활용하는 경우는 6.8에서 알아본다고 한다.

6.5 Memory usage

• 각 자료구조마다 사용하는 key-value pair 형식이 다르기 때문에, 메모리 사용량의 직접 비교보다는 memory overhead를 비교하기로 했다고 함.
• memory overhead는 key-value pair이 사용하는 메모리를 제외한 메모리 사용량이다. key-value pair을 가리키는 pointer도 overhead에 포함.
• 구현한 cuckoo trie는 automatic resizing을 지원안해서 load factor(M)을 85%로 설정했다고 한다. (이전의 실험들도 동일)
• 대신 automatic resizing 적용시 예측되는 메모리 사용량 계산은 했다. 그 값은 (1+K)*M/2라고 한다. K는 increase factor로 논문에서는 2를 사용.
• 그래프를 보면 일반 Cuckoo Trie는 ARTOLC, Wormhole보다 사용량이 최대 28% 낮고, HOT, STX보단 사용량이 최대 156%더 많다. automatic resizing 적용시 더 사용량이 늘어나지만, 그래도 ARTOLC랑 Wormhole과 비교할만하다고 한다.
• 이 결과는 cuckoo-trie가 MLP관련 성능과 memory 효율성 사이에서 균형을 찾는다는 점을 보여준다.

6.6 Memory bandwidth usage

• hardware limit으로 인해 Cuckoo Trie에 bottleneck이 생길지에 관한 내용.
• YCSB-C multithread, rand-8 dataset.
• Index size가 LLC 종합보다 100배정도 더 크기 때문에 대부분 DRAM에서 index 접근이 이루어질거고, 그래서 목표로 하는 측정이 가능.
• 결론은 NUMA interconnect 관련 UPI나 DRAM의 bandwidth 모두 hardware limit대비 많이 적게 활용.

6.7 Comparison with MlpIndex

• MLP를 적극 활용하는 index로 MlpIndex라는 것도 있다.
• hashed trie 기반, 8-byte key만 지원, range scan/multithreading 지원 X
• 그래서 8-byte key로 single thread 기준실험을 해보면 insert/lookup이 MlpIndex가 cuckoo trie보다 성능이 항상 더 좋게 나옴 (30~80%)
  • 8-byte key를 활용한다는 점을 활용해 leaf에 key를 직접 embedding, 이를 통해 memory access를 1회 더 줄이기 때문 (pointer dereference 관련 access를 줄임)
  • 하지만 node크기가 훨씬 크고, key elimination이 존재하지 않아 메모리 사용률도 거의 3배나 더 많다.

6.8 Full-system benchmark

• Redis의 sorted set이라는 ordered index 관련 API를 통해 cuckoo trie 및 benchmark용 index를 redis에서 사용할 수 있도록 설정. YCSB로 실험.
• network/storage delay를 없애기 위해 client/server이 같은 processor의 다른 core에 동작을 하고 DB를 disk에 backup하는 기능을 끔.
• thread 4개 사용. 실험해보니 가장 좋은 성능이 나온다고 해서.
• A~D의 workload에 대해서 az제외 가장 좋은 성능을 보인다. (az 성능이 안나오는 이유는 6.2 참고)
• C의 경우 lookup만 있는데, redis 성능과 비슷하게 나온다. redis의 skip list를 cuckoo trie로 대체해도 괜찮다, 즉 hash table을 필요로 하지 않게 되어 redis의 기존 성능은 유지하면서 메모리 효율성을 높이는게 가능하다고 주장.
• E의 경우 az 제외 타 최고 성능 index structure들과 견줄만한 성능을 보임. E는 scan heavy workload임에도 불구하고 비슷한 성능을 보이는데, 이는 4.4에서 택한 전략이 잘 먹힌다는 것을 의미.