경로 탐색 알고리즘

• 경로 탐색 알고리즘은 컴퓨팅 분야의 많은 응용 프로그램에서 발견할 수 있는 강력한 도구.
• 매커니즘을 짧게 알아 보고 어디에 사용되고 어떻게 동작되는지 이해하는 데 중점

너비 우선 탐색(breadth-first search, BFS)

• 그래프를 탐색하는 알고리즘

• 시작 노드에서 가장 가까운 노드부터 시작하여 모든 노드를 광범위하게 탐색

• 기본적으로 0층에서 시작하며 다음 층으로 이동. 한번 거친 노드 순서를 저장한 후 다시 꺼내는 선입선출 원칙으로 탐사한다. 'Queue' 데이터 구조로 구현하는 편이다

  

  숫자가 나오는 순서대로 탐색이 이루어짐. 각 노드의 층별로 탐색이 이루어 지는 것을 확인 할 수 있다

깊이 우선 탐색(depth-first search, DFS)

• 그래프 탐색 알고리즘

• 시작 노드와 직접 연관된 하위 노드의 끝까지 모두 탐색한 후 다음 하위 노드를 탐색

• 일단 경로 하나의 모든 층을 탐색한 후 그 다음 다른 경로의 모든 층을 탐색. 깊이 우선 탐색을 구현할 때는 보통 재귀 호출이나 스택을 명시하는 방법 사용.

  

  백트래킹
  백트래킹은 모든 경우를 다 탐색해 문제의 해답을 찾는 제어 알고리즘. 어떤 규칙으로 정해진 해답을 찾지 못하면 다시 처음으로 돌아와 다른 규칙으로 문제의 해답을 찾는다. 보통 트리 데이터 구조에서는 깊이 우선 탐색과 너비 우선 탐색을 이용해 백트래킹을 실행한다.

  데이크스트라 알고리즘(Dijkstra's Shortest Path)

• 그래프의 노드로 문제를 표현하면 노드 사이의 최단 경로를 찾음으로써 문제의 해결책을 얻을 수 있다.

• 데이크스트라 알고리즘은 가중 그래프에서 동작하고 그래프의 노드 하나에서 다른 노드까지의 최단 경로를 찾는다.

• 데이크스트라 알고리즘에서는 그래프의 가중치를 Cost라 하며, 알고리즘이 동작하기 위해서는 비용이 음수가 아니어야 한다.

한계점

• 알고리즘이 탐색하는 공간에 대한 정보가 없어서 블라인드 탐색(무정보 탐색)을 수행하는 데 많은 시간과 자원을 소비한다는 한계점이 있다

한계점을 개선한 알고리즘이 여럿 있는데 그 중 벨먼-포드 알고리즘은 그래프에서 최단 경로를 찾는데 사용되며 가중 그래프를 탐색한다는 점은 데이크스트라 알고리즘과 같다.

A*(A star) 알고리즘

• 로봇 공학과 인공지능에 대해 관심이 급증하면서 주목받고 있는 알고리즘
• 데이크스트라 알고리즘과 마찬가지로 노드 사이의 최단 경로를 찾는다
• A* 알고리즘은 휴리스틱 알고리즘의 범주에 속한다.
• 데이크스트라 알고리즘의 접근법과 탐색할 때마다 최선의 휴리스틱을 찾아서 그에 따라 노드를 탐색하는 최선 우선 탐색(best first search)라는 알고리즘의 요소를 결합

휴리스틱 알고리즘
확률론을 토대로 문제의 대략적인 해결책을 제공. 완벽한 논리가 아닌 사람의 직감으로 판단하는 영역을 그대로 구현하는 방법이므로 실전에서 문제없이 사용할 수 있을 정도로 안정성이 입증되어 있다.

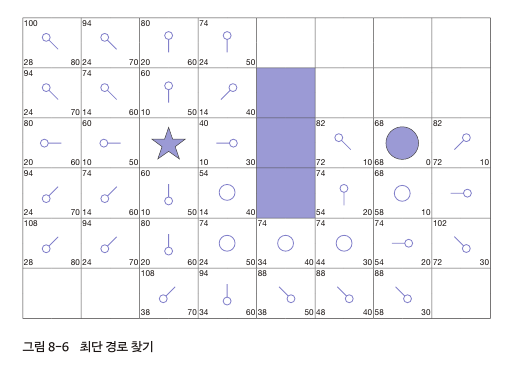
별에서 원으로 이동하려는 경우

• A*알고리즘을 사용하려면 먼저 문제를 그래프로 나태내야한다.
• A*알고리즘은 시작 노드에서 인접 노드로 이동하는 비용을 계산하고 목표 노드까지의 예상 비용을 계산
• 계산이 끝나면 인접 노드 중 비용이 가장 낮은 노드를 선택
• 선택된 노드를 '탐색이 완료된' 노드로 간주한다.
• 어림짐작한 최단 경로의 비용이 실제 최단 경로의 비용에 가까울 수 있어 더 효율적이다. 물론 비용 계산이 실패할 수도 있음. 다만 적어도 최단 경로를 찾는 것이 보장됨