[하버드 확률론 기초 : Statistics 110] 2강 - 해석을 통한 문제풀이 및 확률의 공리 (Story Proofs, Axioms of Probability)
0
[하버드 확률론 기초 : Statistics 110]
목록 보기
2/5

- 표본추출을 정리한 표(Sampling Table): n개 중에서 k개 뽑기

다른 경우들은 곱의 법칙으로 설명이 되지만, (복원, 순서 상관이 없는) 경우 그렇지 않음.
n개에서 k개를 순서 상관 없이, 복원하며 뽑는 경우의 수:
→ 숫자 대입해서 확인해보기
- (일반적인 경우) k=1 대입:
- (극단적인 경우) k=0 대입:
- (간단하지만 당연하지는 않은 값) n=2 대입:
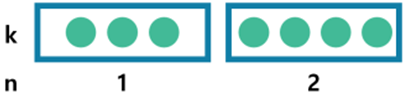
n=2, k=7이라고 했을 때, 첫 번째 상자에 들어갈 수 있는 경우의 수는 0,1,2,...,k개로 k+1가지이다.
→ 일반화: n개의 상자에 k개의 구별 불가능한 object들을 넣을 수 있는 경우의 수는 얼마인가?
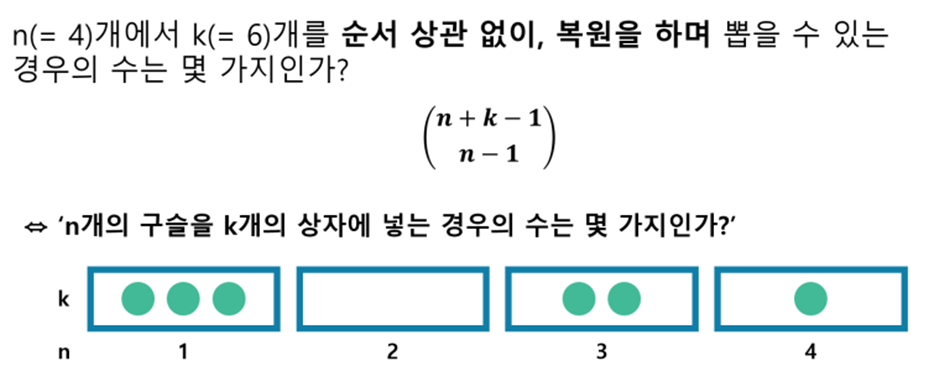
구슬과 같이 실물이 있는 물체는 labeling이 가능하며 서로 구별이 가능하다. 따라서 확률의 naive한 정의로 접근이 가능하다. 하지만 물리학, counting problem에서의 경우에는 object들이 항상 구별 가능한 것이 아니기 때문에 이와 같은 접근이 어렵다.

위 문제는 n+k-1개의 위치에 원과 구분선을 배열하는 것과 같다. 원의 위치를 먼저 정하면 구분선의 위치도 결정되고, 그 반대도 성립하기 때문에, 다음과 같은 등식이 성립함을 확인할 수 있다.
-
Story proof: 상황 해석을 통한 증명 (대수적 방법으로 접근하는 것보다 훨씬 쉬 울 때가 있음!)
- ex 1)
- ex 2)
명 중에서 명 뽑기, 명 중에서 한 명을 회장으로 뽑는 문제로 해
회장을 먼저 뽑고 나머지 명에 들어갈 사람 뽑기 명을 뽑고 그
중에서 회장 뽑기 - ex 3)
개에서 개 뽑기
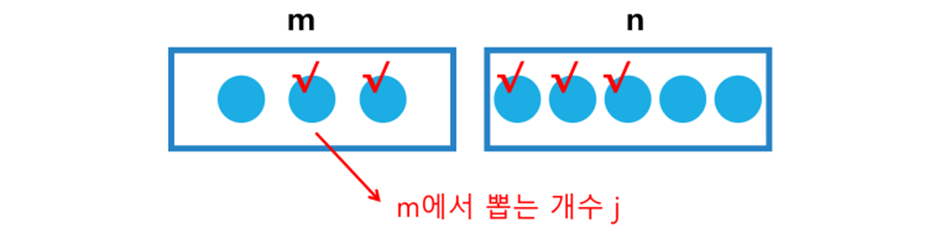
각각의 사건은 disjoint하기 때문에 모두 더하면 된다.
-
Non-naïve definition of probability
- 확률공간(Probability space) → S와 P로 구성됨
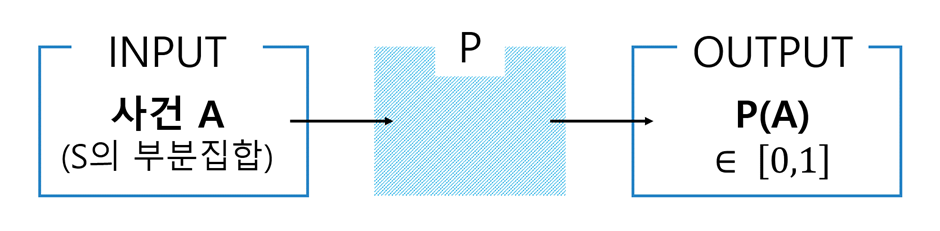
- 확률공간(Probability space) → S와 P로 구성됨
-
공리
- 는 서로소이다.)
두 가지 공리로부터 대부분의 식을 유도할 수 있음!
본 포스트의 학습 내용은 boostcourse 내의 [하버드] 확률론 기초: Statistics 110 (Prof. Joe Blitzstein) 강의 내용을 바탕으로 작성되었습니다.
(https://www.edwith.org/ai152)
