
📖 Convolution 연산 이해하기
- 지금까지 배운 다층신경망(MLP)은 각 뉴런들이 선형모델과 활성함수로 모두 연결된(fully connectec) 구조였습니다.
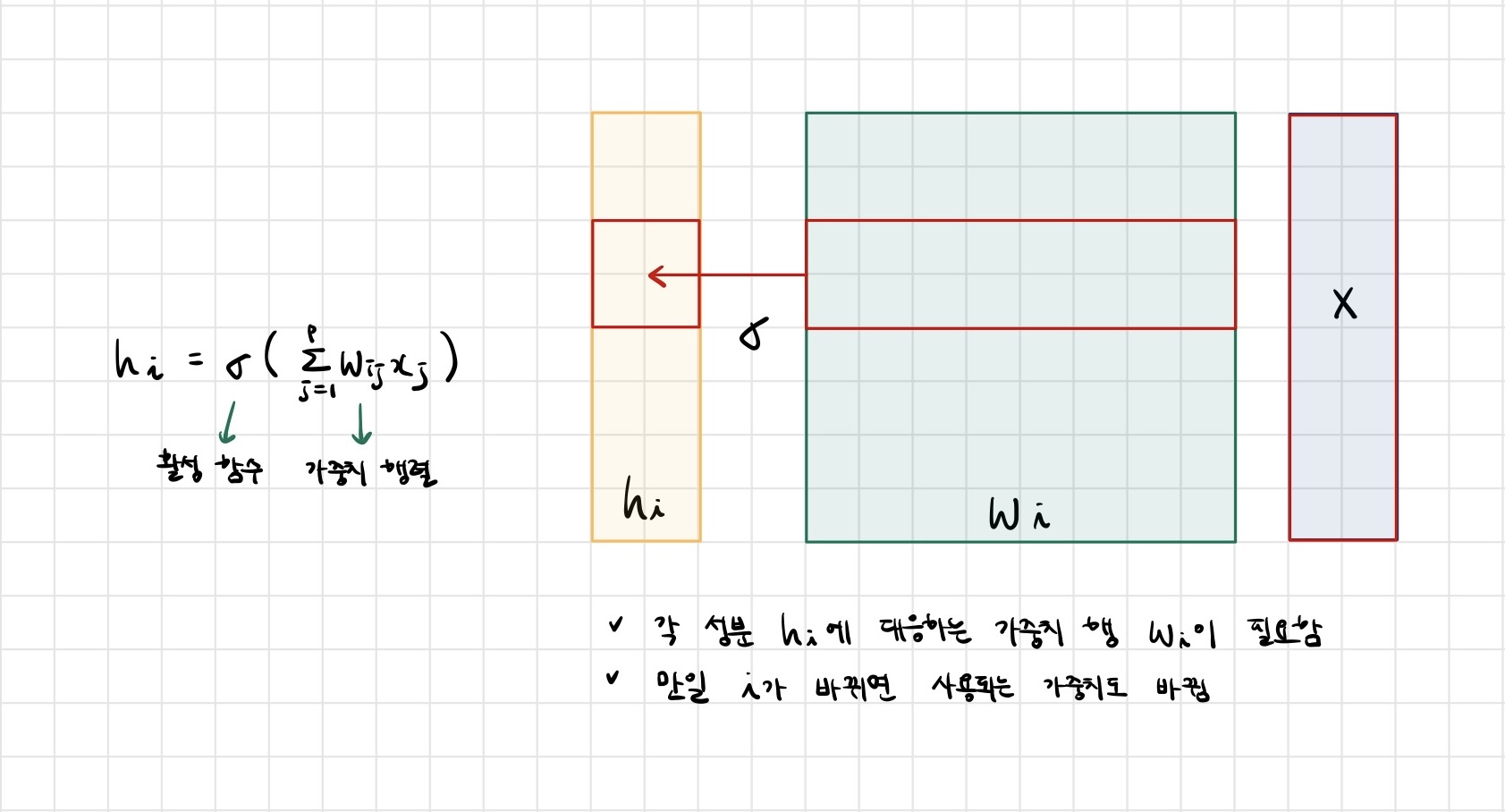
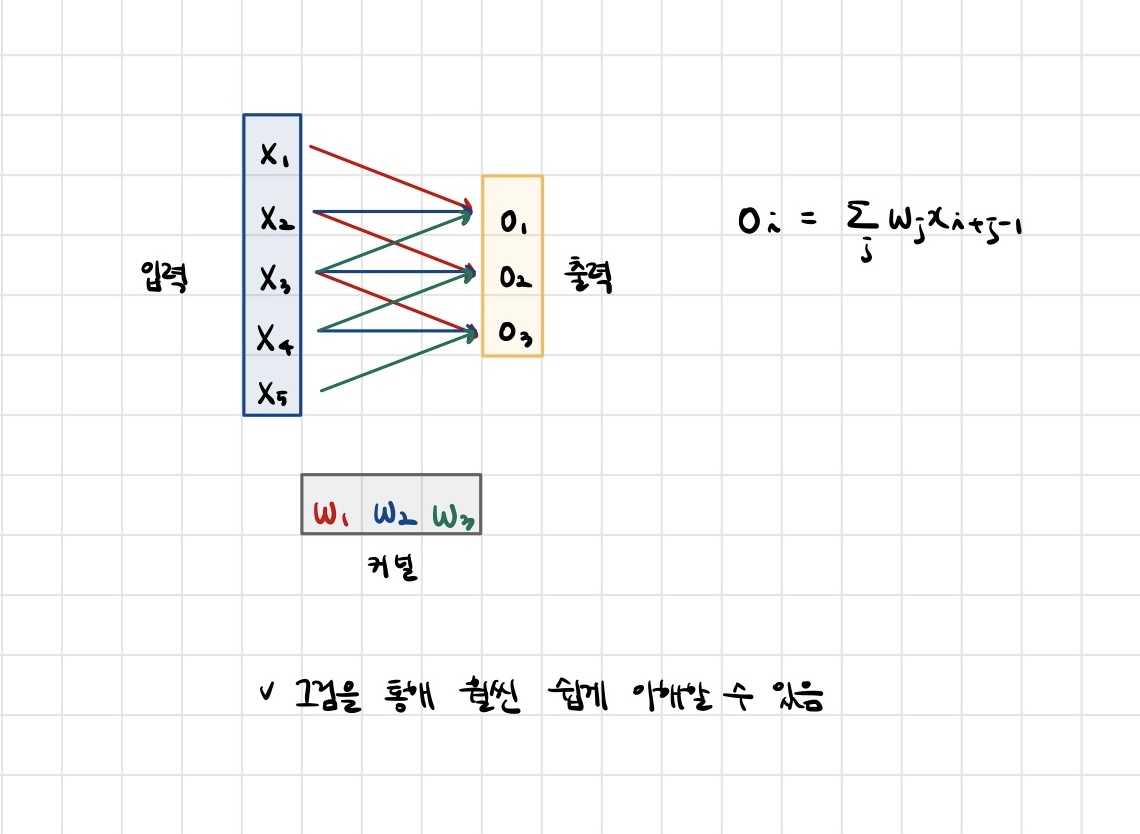
- Convolution 연산은 이와 달리 커널(kernel)을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조입니다.
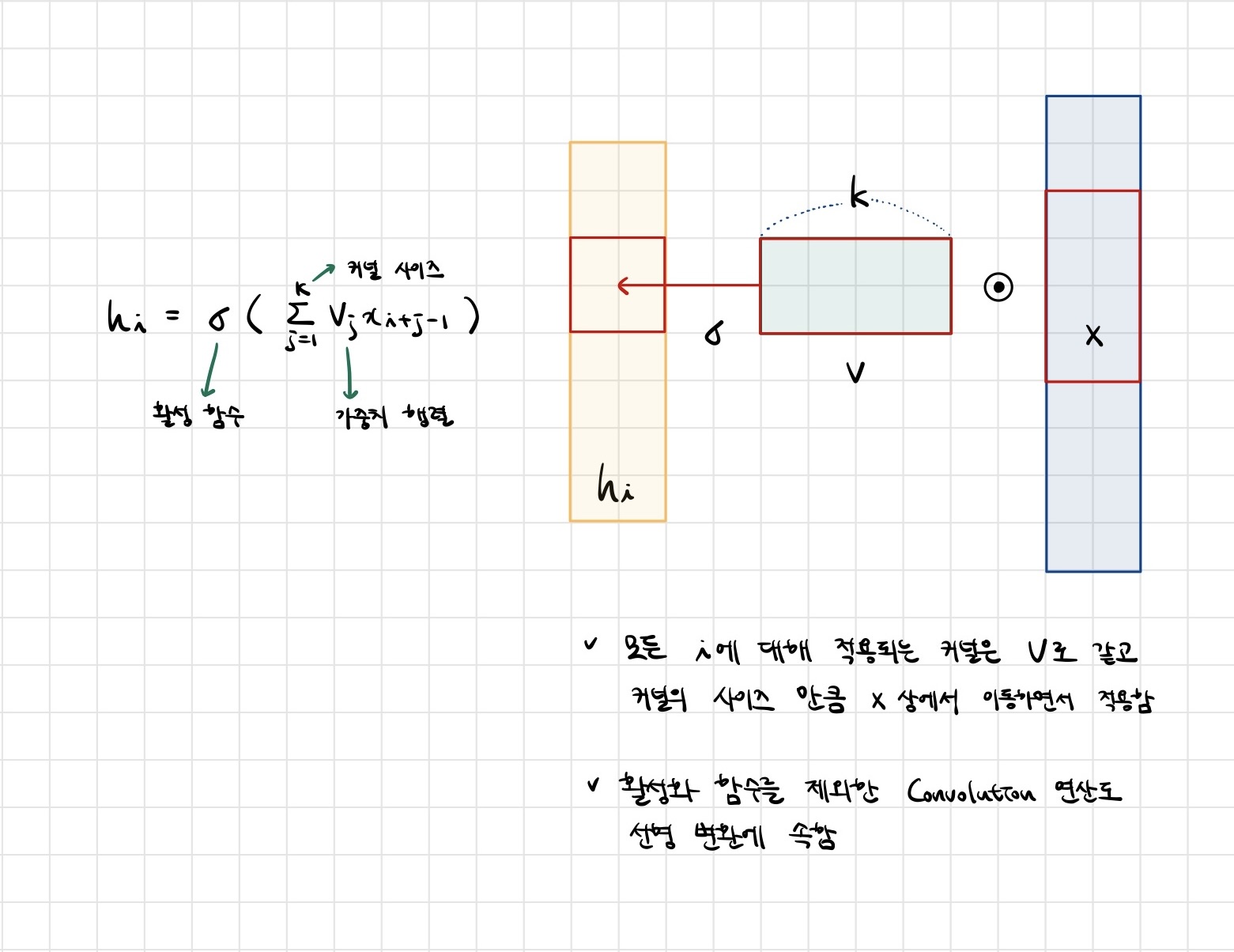
- Convolution 연산의 수학적인 의미는 신호(signal)를 커널을 이용해 국소적으로 증폭 또는 감소시켜서 정보를 추출 또는 필터링하는 것입니다.

- 커널은 정의역 내에서 움직여도 변하지 않고(translation invariant) 주어진 신호에 국소적(local)으로 적용합니다.
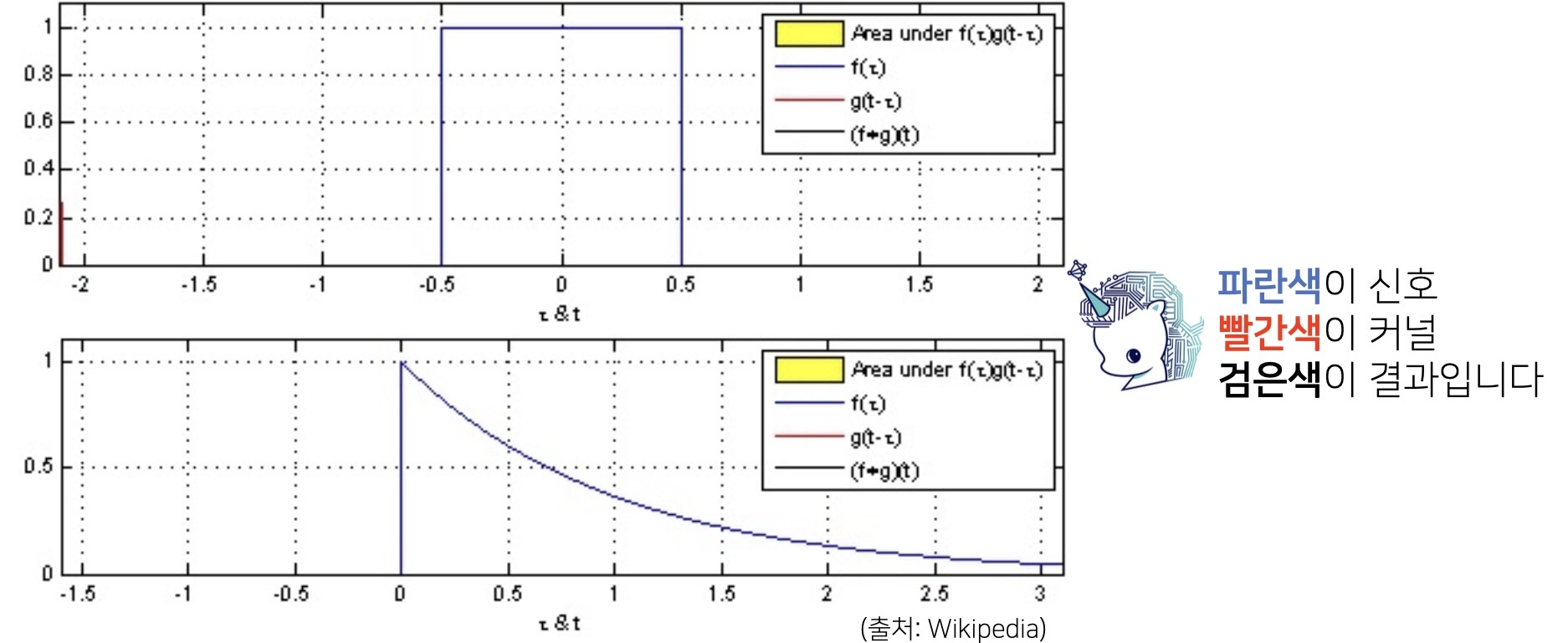
📖 영상처리에서 Convolution
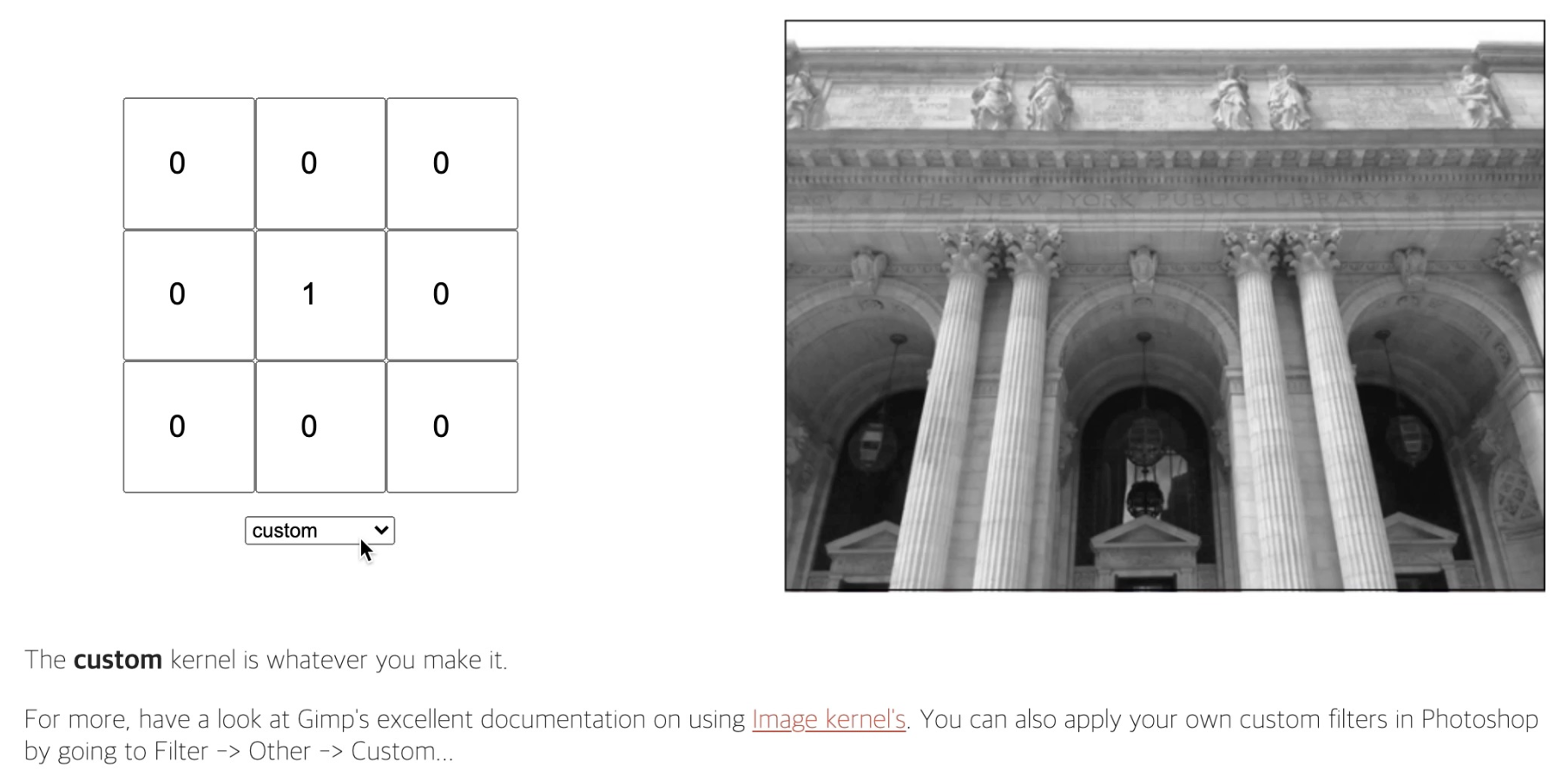
📖 다양한 차원에서의 Convolution
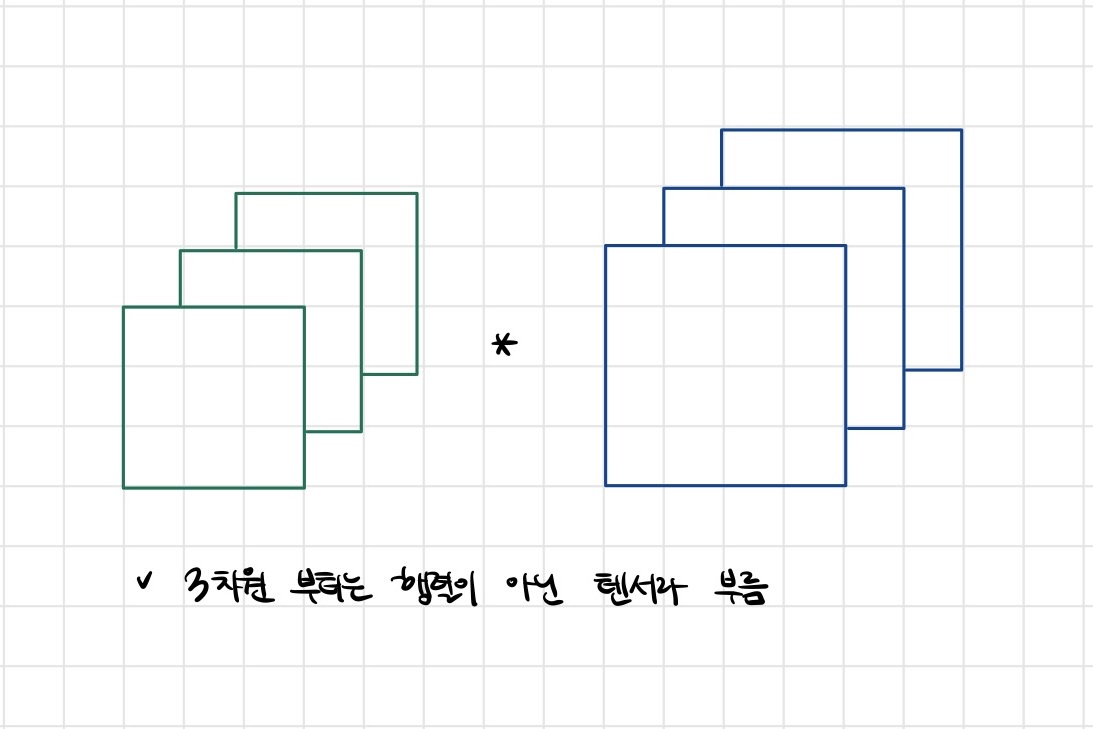
- Convolution 연산은 1차원뿐만 아니라 다양한 차원에서 계산 가능합니다.

📖 2차원 Convolution 연산 이해하기
- 2D-Conv 연산은 이와 달리 커널(kernel)을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조입니다.
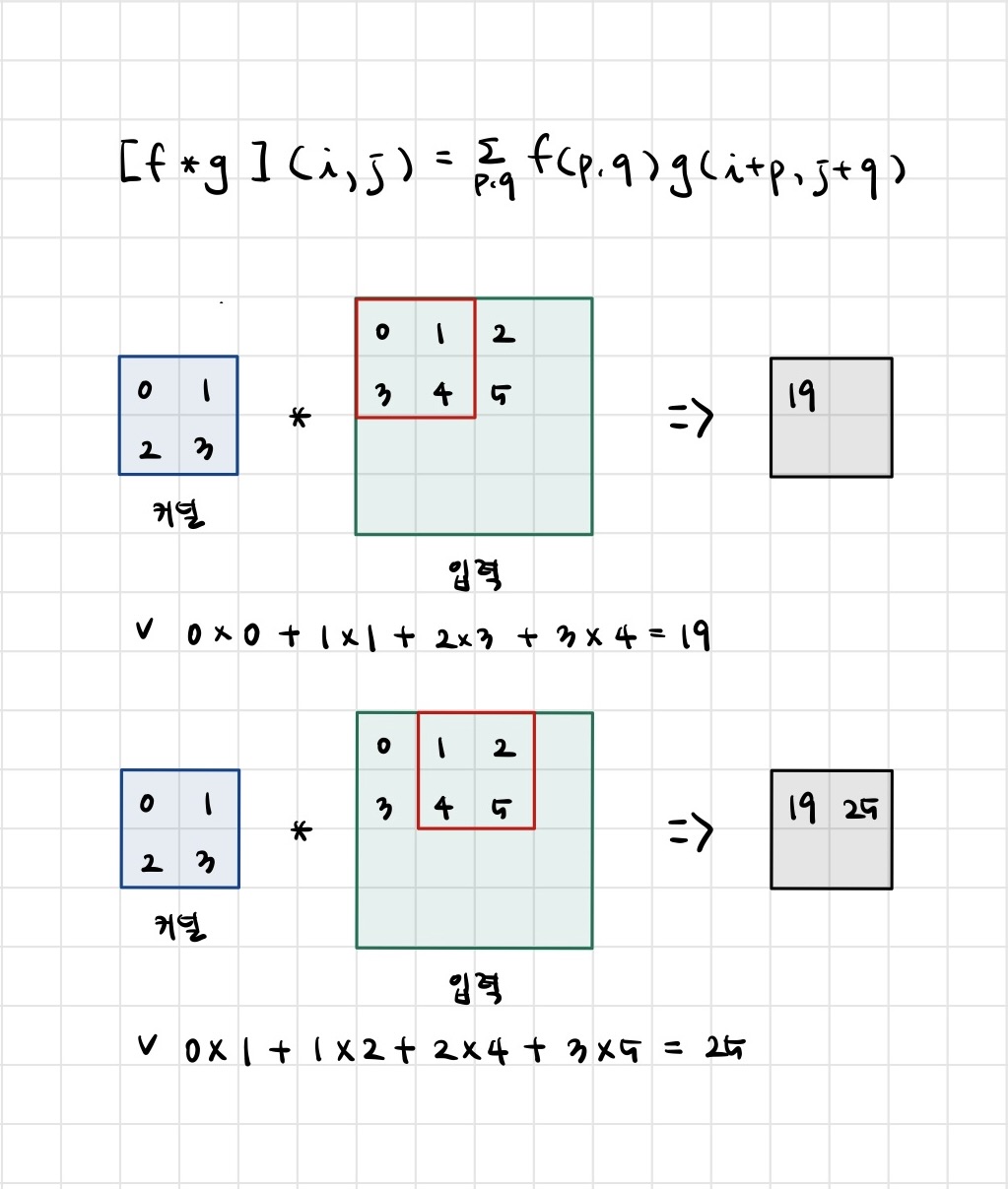
- 입력 크기를 , 커널 크기를, 출력 크기를 라 하면 출력 크기는 다음과 같이 계산합니다
- 가령 28 x 28 입력을 3 x 3 커널로 2D-Conv 연산을 하면 26 x 26 이 된다.
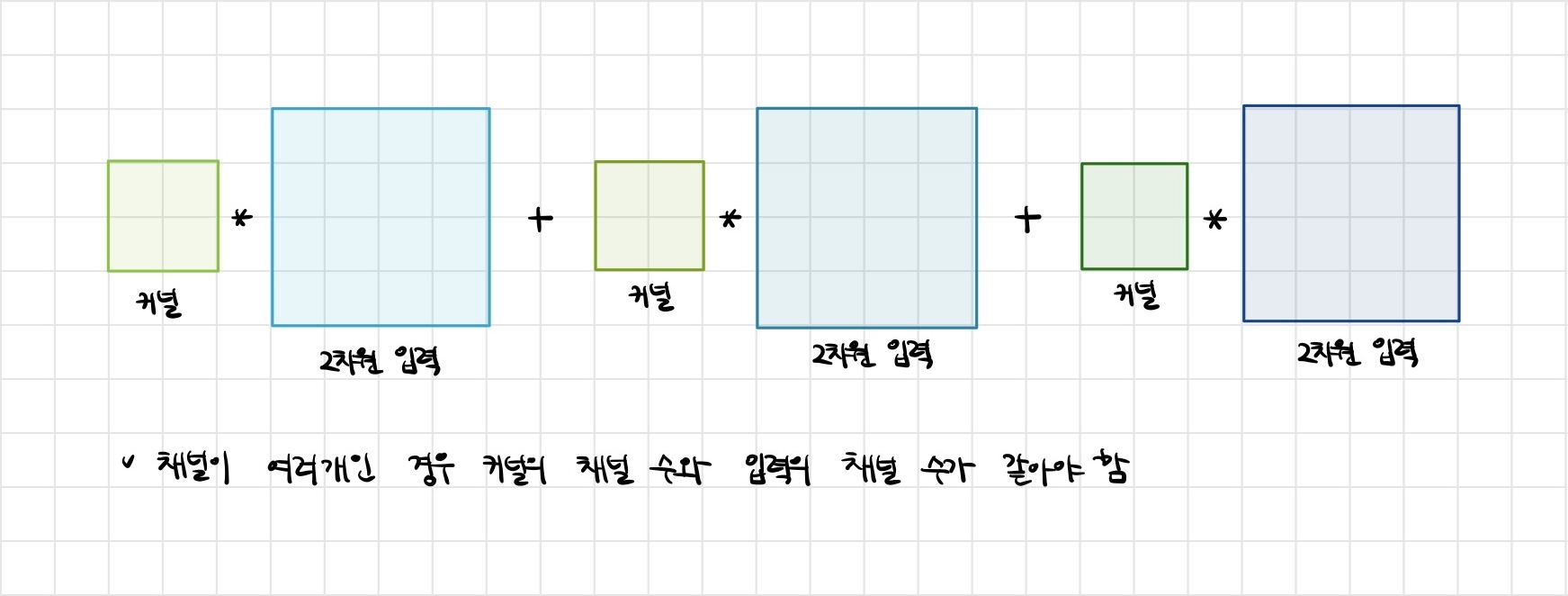
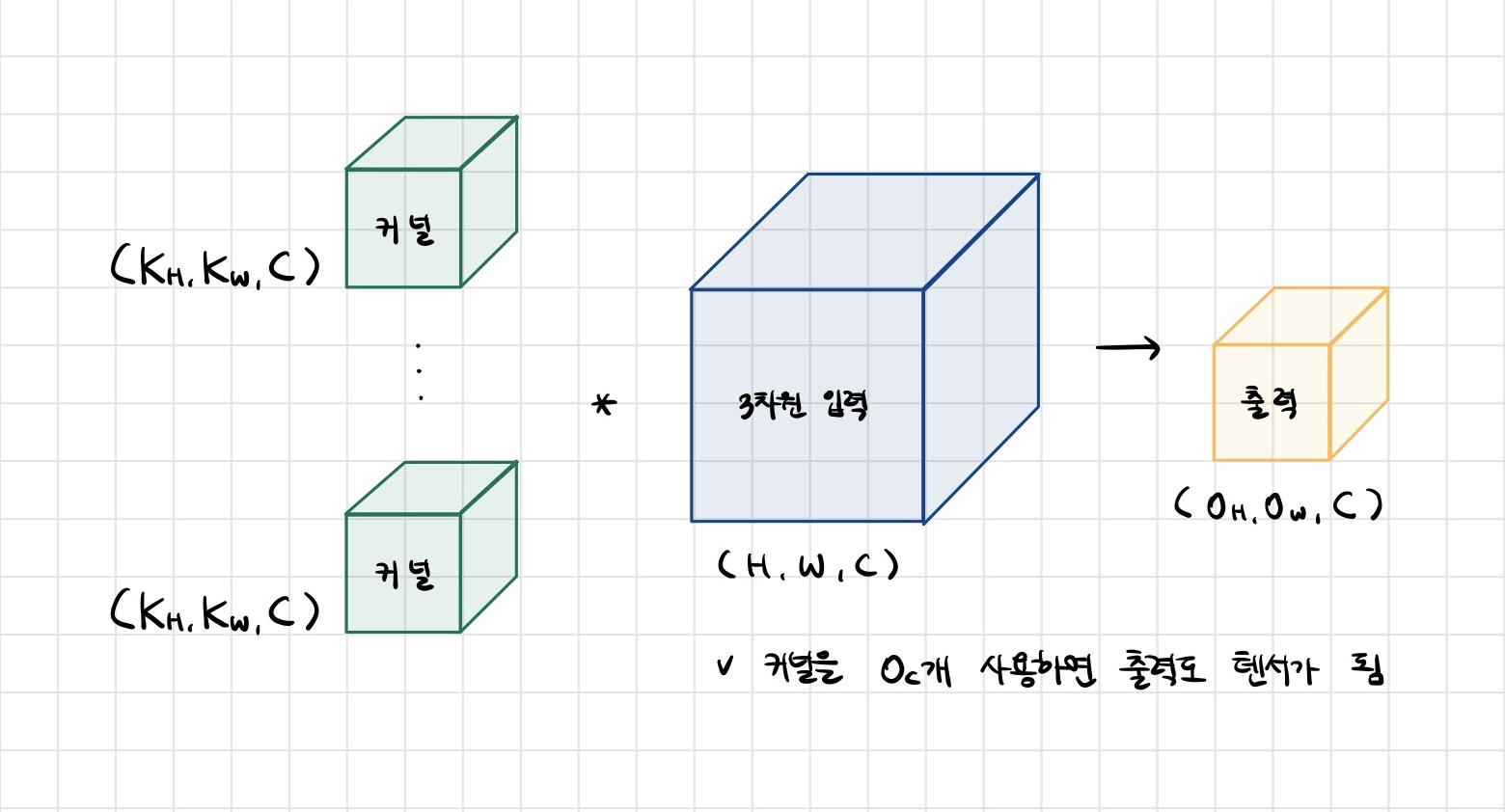
- 채널이 여러개인 2차원 입력의 경우 2차원 Convolution을 채널 개수만큼 적용한다고 생각하면 됩니다.
📖 Convolution 연산의 역전파 이해하기
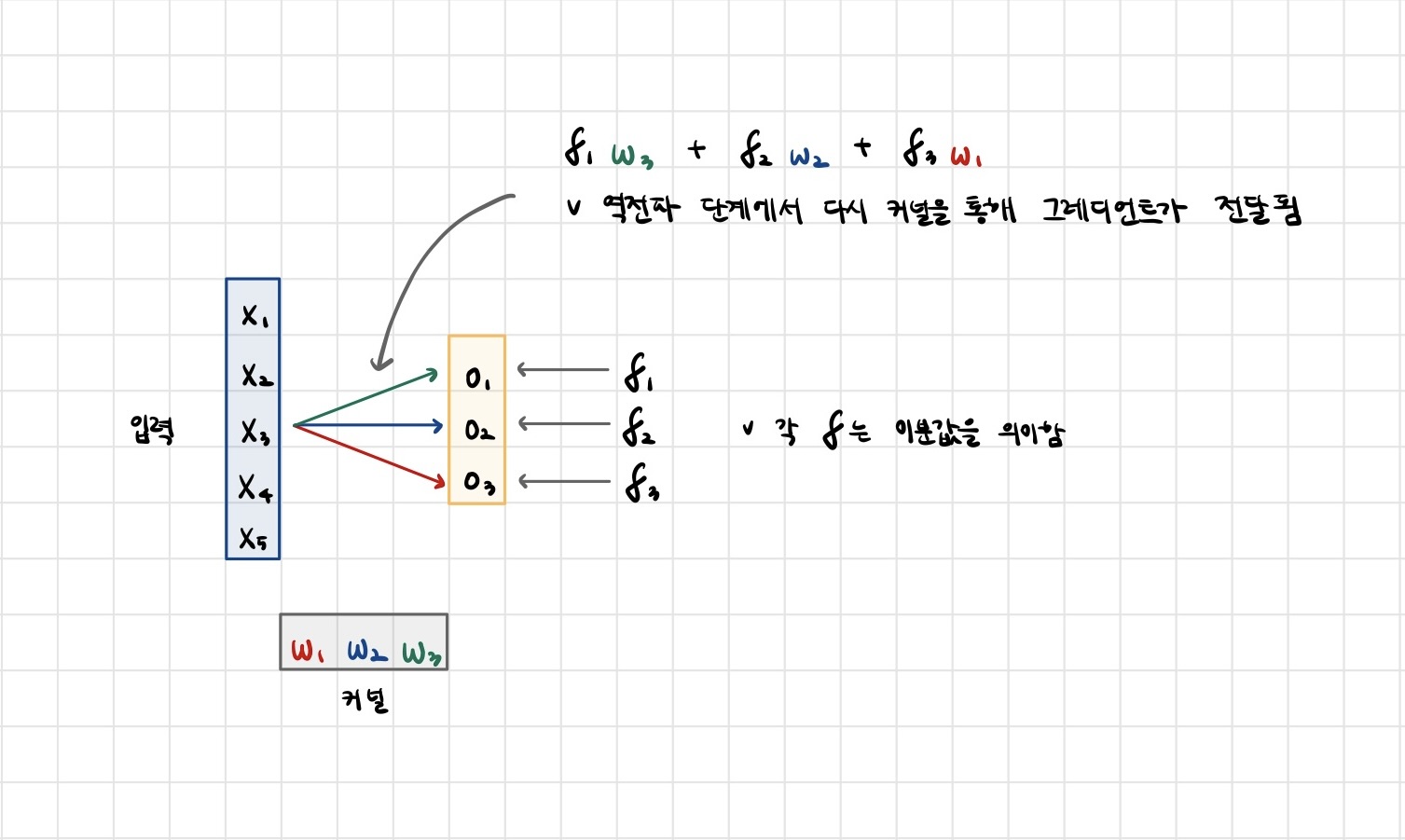
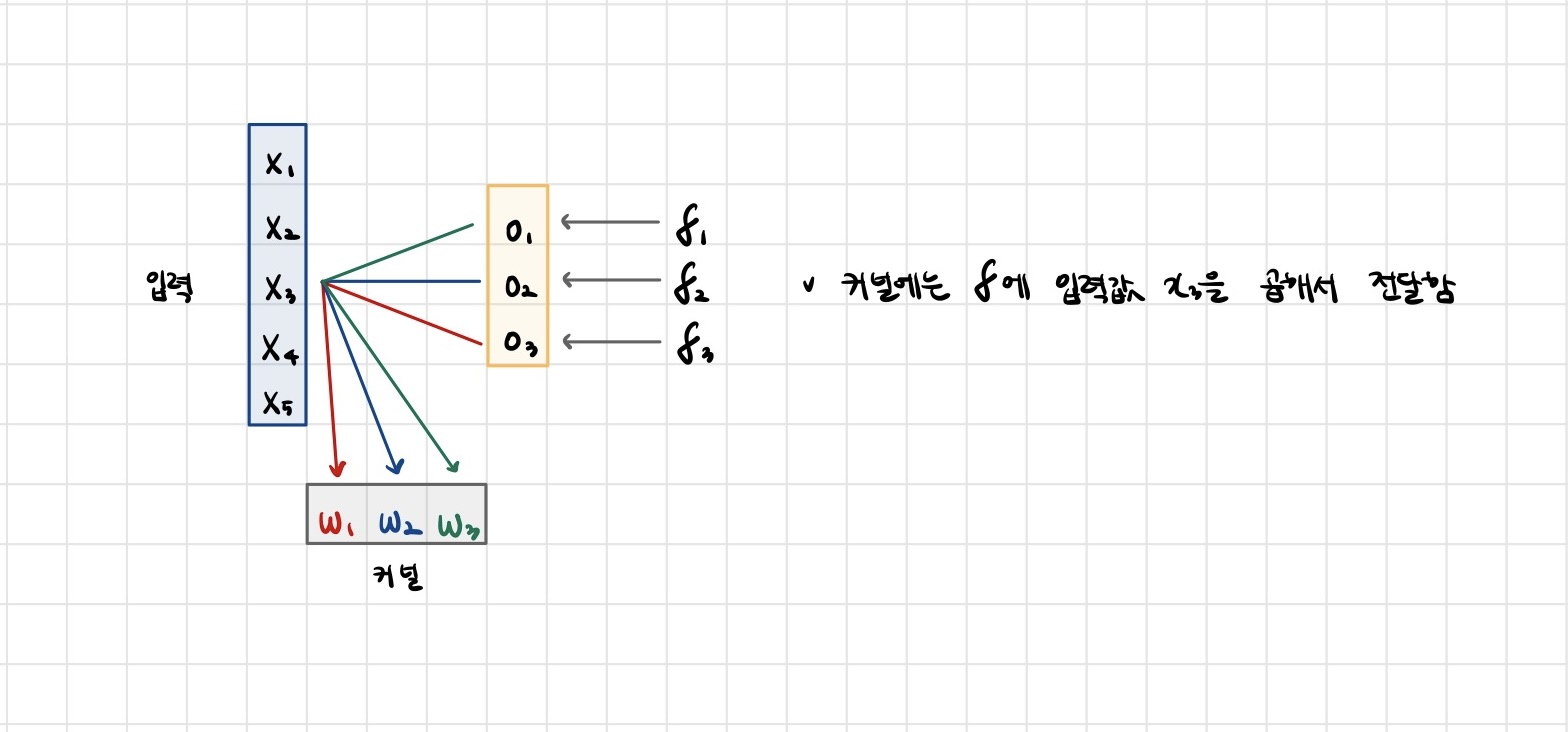
- Convolution 연산은 커널이 모든 입력데이터에 공통으로 적용되기 때문에 역전파를 계산할 때도 convolution 연산이 나오게 됩니다.
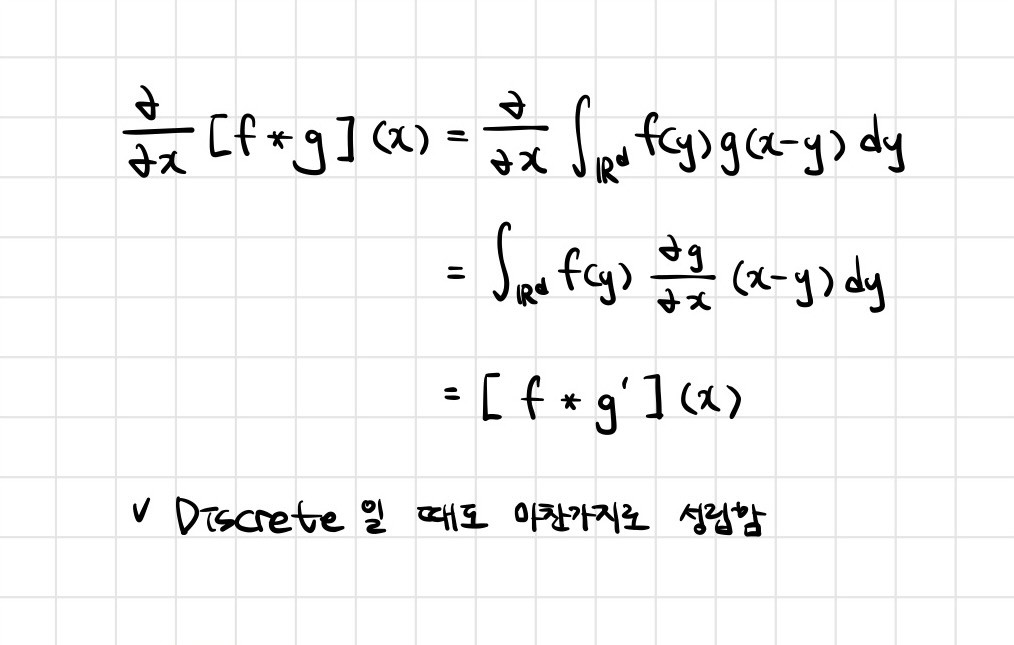

<이 게시물은 임성빈 교수님의 'CNN 첫걸음' 강의 자료를 참고하여 작성되었습니다.>
본 포스트의 학습 내용은 [부스트캠프 AI Tech 5기] Pre-Course 강의 내용을 바탕으로 작성되었습니다.
부스트캠프 AI Tech 5기 Pre-Course는 일정 기간 동안에만 운영되는 강의이며,
AI 관련 강의를 학습하고자 하시는 분들은 부스트코스 AI 강좌에서 기간 제한 없이 학습하실 수 있습니다.
(https://www.boostcourse.org/)
