학습 관련 기술들

매개변수 갱신

확률적 경사 하강법 (SGD)

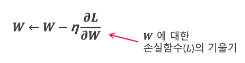
매개변수의 기울기를 구하고 기울어진 방향으로 매개변수 값을 갱신하는 일을 반복하여 최적의 값을 찾는 것

단순하고 구현하기 쉽지만 문제에 따라 비효율적일 수 있음

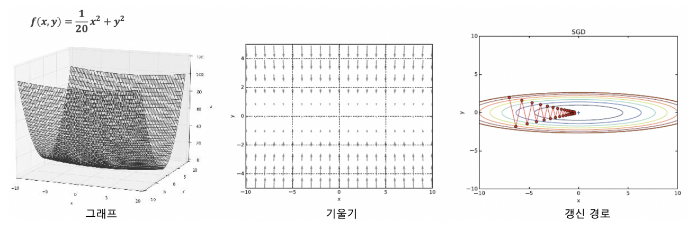
• 위 그림에서 y축 방향은 가파른데 x축 방향은 완만
• 최솟값이 되는 장소는 (0,0)이지만, 기울기 대부분은 그곳을 가리키지 않음
• 갱신 경로가 상당히 비효율적인 움직임

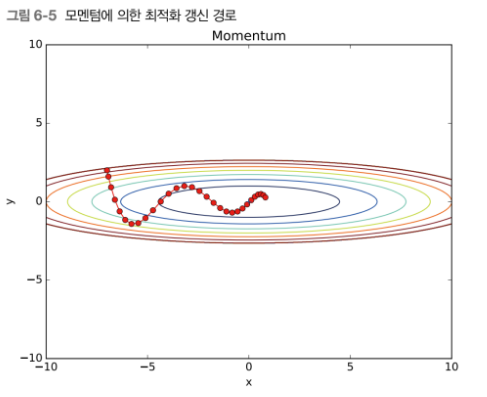
모멘텀

모멘텀은 운동량을 뜻하고 수식은 아래와 같음

v는 속도를 뜻함

AdaGrad

신경망에서는 학습률이 중요함

이 학습률을 정하는 효과적 기술로 학습률 감소가 있음 → 학습을 진행하면서 학습률을 조금씩 줄여감

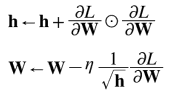
• h는 기존 기울기 값을 제곱하여 계속 더해줌
• 매개변수를 갱신할 때 1/sqrt(h)를 곱하여 학습률을 조정
• 과거의 기울기를 제곱하여 계속 더해가기 때문에 학습을 진행할수록 갱신 강도가 약해짐
  

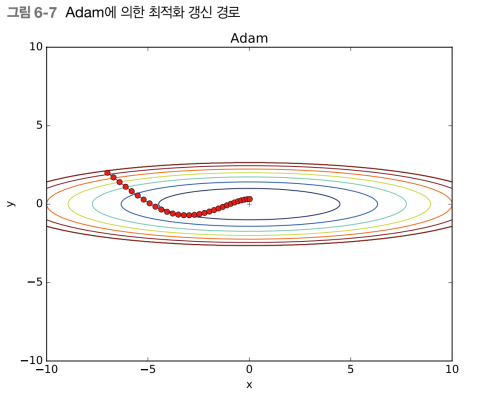
Adam

모멘텀 + Adagrad

매개변수 공간을 효율적으로 탐색하며 하이퍼파라미터 편향 보정이 진행됨

네가지 방법 비교

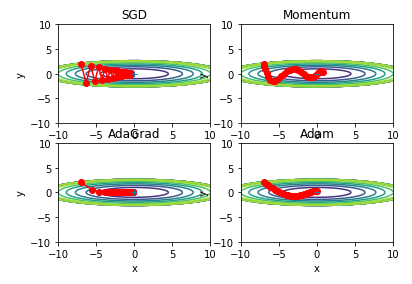
위 함수에서는 AdaGrad가 가장 좋아보임

위 네가지 갱신 방법 중 어떤것이 나은가에 대한 정답은 없음

각 상황에 따라 결과가 다르게 나타남

가중치의 초깃값

초깃값을 0으로 하면?

• 가중치 감소 기법 : 가중치 매개변수의 값이 작아지도록 하여 오버피팅이 일어나지 않도록 하는 기법
• 가중치를 작게 만들고 싶으면 초깃값도 작은 값에서 시작 --> 0으로 설정은 안됨
• 초깃값을 0으로 설정하게 되면 오차역전파에서 모든 가중치값이 독같이 갱신되기 때문
• 순전파 때 모든 뉴런에 같은 값이 입력되므로, 역전파 두번째 층의 가중치가 모두 똑같이 갱신된다는 뜻(학습이 안됨)
• (가중치를 균일한 값으로 설정X) 가중치 초깃값을 무작위로 설정해야함

가중치의 표준편차를 1로 잡았을 때

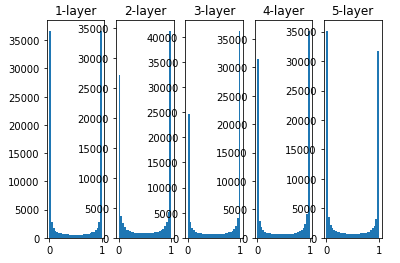
• 각 층의 활성화 값들이 0과 1에 치우쳐 있음
• 시그모이드 함수는 출력이 0 (또는 1)에 가까워지자 그 미분은 0에 다가감
• 기울기 소실 : 데이터가 0과 1에 치우쳐 분포하게 되면 역전파의 기울기 값이 점점 작아지다가 사라짐

가중치의 표준편차를 0.01로 잡았을 때

• 0.5 부근에서 값 집중
• 기울기 소실 문제는 없으나, 활성화 값이 치우친 것은 표현력 관점에서 큰 문제
• 노드 100개가 거의 같은 값을 출력한다면 노드가 많아도 노드 하나 모델과 다를게 없음

Xavier 초깃값

• 일반적인 딥러닝 프레임워크에서 표준적으로 이용하는 초깃값
• 앞 계층의 노드가 n개라면 표준편차가 1/sqrt(n) 분포를 사용하면 된다는 것을 이용
• 앞 층의 노드가 많을수록 대상 노드이 초깃값으로 설장하는 가중치가 좁게 퍼짐
  
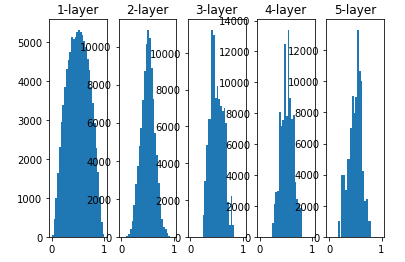
• 층이 깊어지며 형태는 일그러지지만 앞 방식보다 넓게 분포됨
• 각 층의 데이터가 적당히 퍼져있으므로 함수의 표현력 제한 받지 않고 효율적 학습 진행

Relu 사용 시 가중치 초깃값

• ReLU 이용 시에는 ReLU에 특화된 초깃값 이용 권장
• He 초깃값 : 앞 층의 노드가 n개 일 때, 표준편차가 sqrt(2/n)인 정규분포 사용
• ReLU는 음의 영역이 0이기 때문에 더 넓게 분포시키기 위해 2배의 계수가 필요
• ReLU를 이용한 경우 활성화 값 분포 (0.01std, Xavier, He)
  
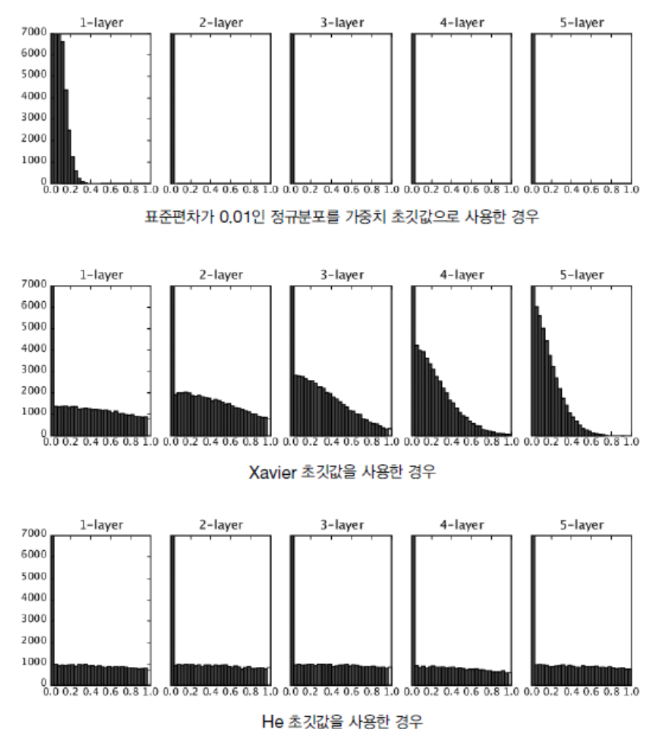
• std=0.01일 때의 각 층의 활성화 값들은 아주 작은 값
• 신경망에 아주 작은 데이터가 흐른다는 것은 가중치의 기울기 역시 작아져 학습이 제대로 이루어지지 않음
• Xavier는 층이 깊어지면서 치우침이 조금씩 커짐 = 기울기 소실문제 일으킴
• He초깃값은 모든 층에서 균일분포 = 역전파 때도 적절값 나올 가능성 높음
• ReLU 사용 시 He, sigmoid, tanh 등의 S자 모양 곡선에서는 Xavier초깃값 사용

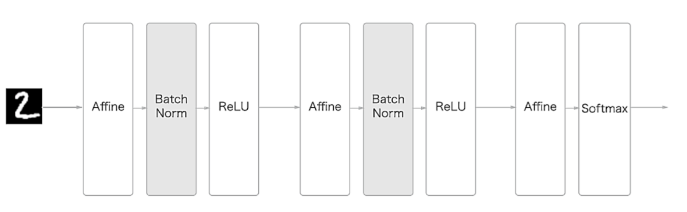
배치 정규화

• 각 층이 활성화를 적당히 퍼뜨리도록 하는 방법

• 배치 정규화가 주목받는 이유

  1. 학습 속도 개선
  2. 초깃값에 크게 의존하지 않음
  3. 오버피팅 억제 (드롭아웃 등 필요성 감소)

• 배치 정규화 과정

  1. 배치 정규화 계층 신경망에 삽입
  2. 학습 시 미니배치를 단위로 정규화 (데이터 분포 평균 0, 분산이 1이 되도록)

Overfitting

신경망이 훈련 데이터에만 지나치게 적응되어 그 외의 데이터에는 제대로 대응하지 못하는 상태

Overfitting은 주로 2가지 경우에 일어남

• 매개변수가 많고 표현력이 높은 모델
• 훈련 데이터가 적을 경우

가중치 감소

학습 과정에서 큰 가중치에 대해서는 큰 페널티를 부과하여 overfitting을 억제하는 방법

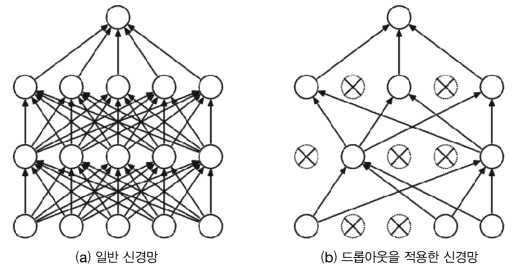
드롭 아웃

뉴런을 임의로 삭제하면서 학습하는 방법

적절한 하이퍼 파라미터 값 찾기

검증 데이터

• 하이퍼 파라미터 성능 평가시에는 test data 사용해서는 안됨
• 검증데이터(validation data) : 하이퍼 파라미터 검증용 데이터

하이퍼 파라미터 최적화

• 하이퍼파라미터 최적화의 핵심은 하이퍼파라미터의 '최적 값'이 존재하는 범위를 조금씩 줄여간다는 것
• 대략적인 범위 정하고 그 범위에서 무작위로 값을 골라낸 후, 정확도 평가

0. 하이퍼파라미터 값의 범위를 설정
1. 설정된 범위에서 하이퍼 파라미터의 값을 무작위로 추출
2. 1단계에서 샘플링한 하이퍼 파라미터 값을 사용하여 학습하고, 검증 데이터로 정확도를 평가.(단, epoch는 작게 설정)
3. 1단계와 2단계를 특정 횟수 반복하여 그 정확도를 보고 하이퍼 파라미터의 범위를 좁힘