그리디(Greedy) 알고리즘 = 탐욕법

Ch04. 그리디(Greedy) 알고리즘

현재 상황에서 당장 가장 좋아 보이는 상황만을 선택하는 알고리즘

• 최적의 해를 구하기 위한 근사적인 방법으로 사용될 때가 많음 ⇒ 최적의 해에 가까운 근사 해 구할 수 있음

ex) 루트에서 출발하여 단말 노드까지 가는 경우, 거쳐가는 노드의 합이 가장 큰 경우는?

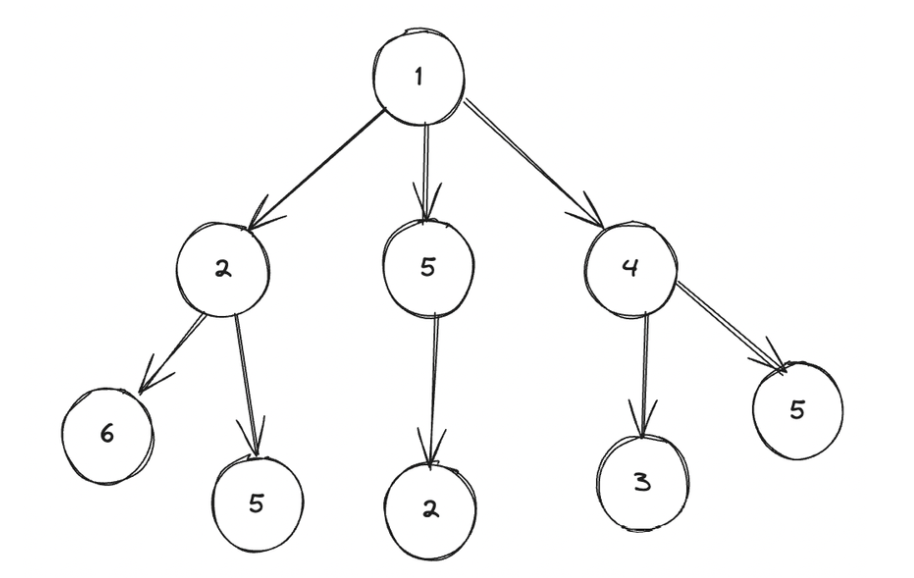
1) 완전탐색으로 풀이

• 최적의 해: 10 (1→4→5)
• 모든 상황을 고려해야 함

2) 탐욕 알고리즘으로 풀이

• 매 상황에서 단순히 가장 큰 노드 선택: 8 (1→5→2)
• 모든 경우의 수를 고려하지 않아도 됨
  • 하지만, 최적의 해는 아님!

탐욕 알고리즘 접근 방법

1. 방법 고안하기: 현재 상황에서 어떤 것을 선택할지 알고리즘을 고안
2. 정당성 확인하기: 자신이 고안한 알고리즘이 항상 최적의 해를 보장 하는지 확인 (증명 단계)

ex) 거스름 돈 문제

문제: 카운터에 500원, 100원, 50원, 10원짜리 동전이 무수히 많이 존재할 때, 손님에게 6,480원을 거슬러 주어야 할 때, 동전 개수의 최솟값은?

해결 방법: 가장 큰 화폐 단위부터 거슬러주는 것 → 500원, 100원, 50원, 10원 순으로 거슬러 줌

[1단계] 500원으로 거슬러 주기 → 6480/500 = 12…480 → 12개

[2단계] 100원으로 거슬러 주기 → 480/100 = 4…80 → 4개

[3단계] 50원으로 거슬러 주기 → 80/50 = 1…30 → 1개

[4단계] 10원으로 거슬러 주기 → 30/10 = 3 → 3개

따라서, 총 12+4+1+3 = 20개

⇒ 화폐 단위가 배수 관계에 속하기 떄문에 그리디 알고리즘을 사용하여 최적의 해 찾을 수 있음

만약, 120원을 거슬러 주어야 할 때, 80원, 60원, 10원 동전이 있다면?

• 최적의 해: 60원 X 2 = 120원으로, 2개의 동전 필요
• 그리디 알고리즘 풀이로 80원부터 거슬러 준다면, 총 5개의 동전 필요

→ 따라서, 위의 문제는 그리디 알고리즘으로 최적의 해 찾을 수 없음