크루스칼(Kruskal) 최소 신장 트리 알고리즘

최소 신장 트리

• 주어진 가중치 그래프에서 사이클 없이 모든 점을 연결 시킨 트리 중 간선들의 가중치 합이 최소인 트리

크루스칼 알고리즘

• 가중치가 가장 작은 간선이 사이클을 만들지 않을 때만 'Greedy' 하게 그 간선을 추가시키는 방법
• 간선 기준으로 최소 신장 트리를 만들어 낸다.

Pseudo Code

KruskalMST(G)
입력: 가중치 그래프 G=(V,E), |V|=n, |E|=m
출력: 최소 신장 트리 T

1. 가중치의 오름차순으로 간선들을 정렬: L = 정렬된 간선 리스트
2. T=NULL
3. while(T의 간선 수 < n-1)
4.	L에서 가장 작은 가중치를 가진 간선 e를 가져오고 e를 L에서 제거
![](https://velog.velcdn.com/images/alsrb5606/post/008e5baa-b368-443e-8703-0466b9fbaf57/image.png)
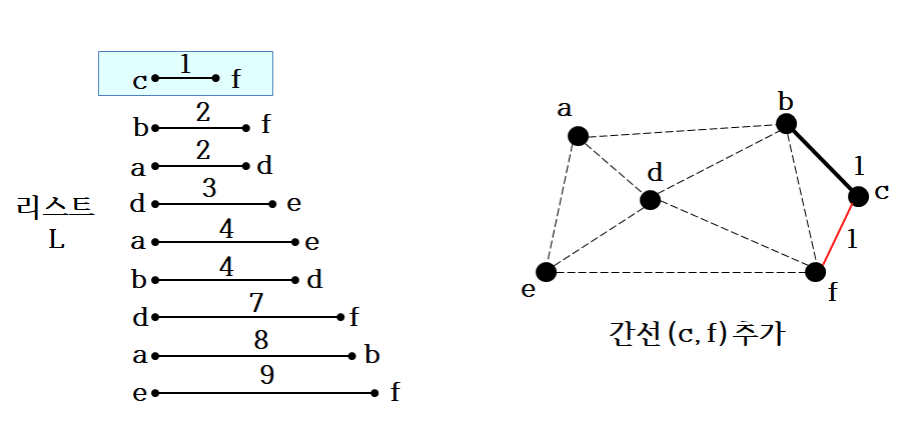
5.	if(간선 e가 T에 추가되어 사이클을 만들지 않으면)
6.		e를 T에 추가
7.	else
8.		e를 버린다.
9.	return 트리 T

KruskalMST 알고리즘 수행 과정

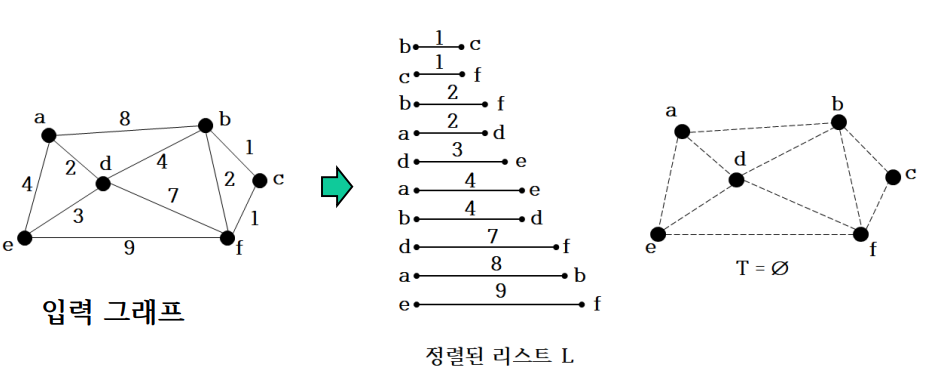
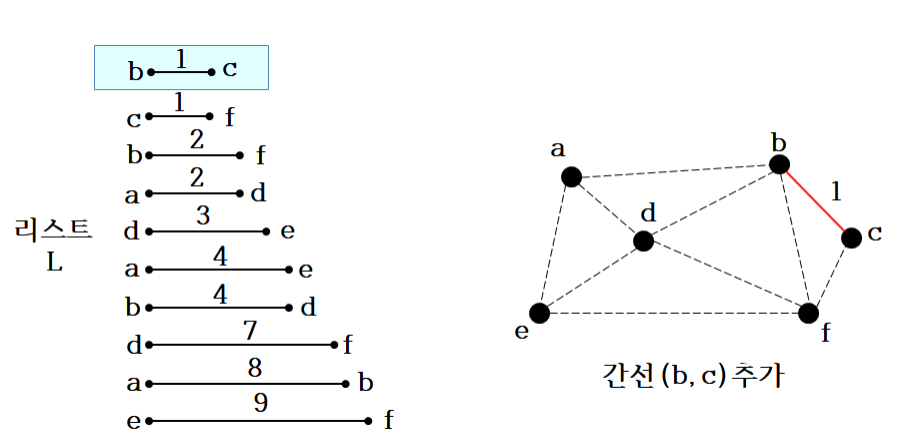
• 위와 같은 방법으로 최소 비용으로 정렬된 간선들을 선택하여 최소 신장 트리를 구성하는데 해당 간선으로 구성할 때 사이클이 만들어지는지 아닌지 확인하여 구성하면 된다.

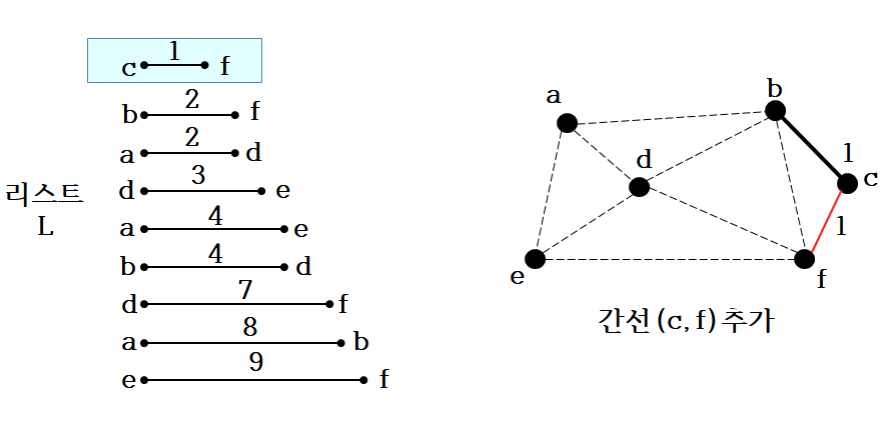
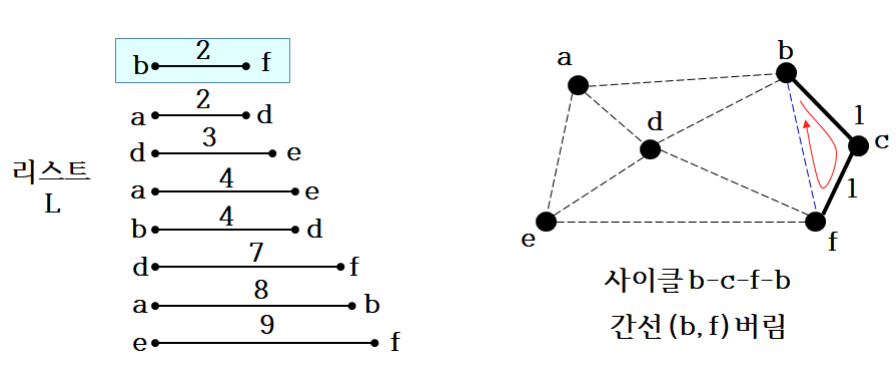
사이클 확인 방법

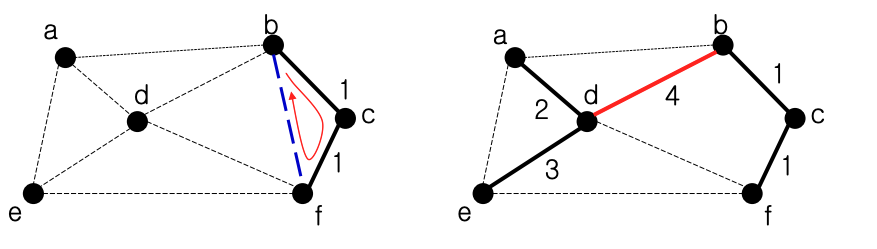
• 만약 (b,f)를 MST에 추가할 때:
  - b,c,f는 같은 그룹

  • 추가하려는 선분의 두 노드가 같은 그룹에 있으면 사이클을 생성하게된다.
    • find(b) == find(f)

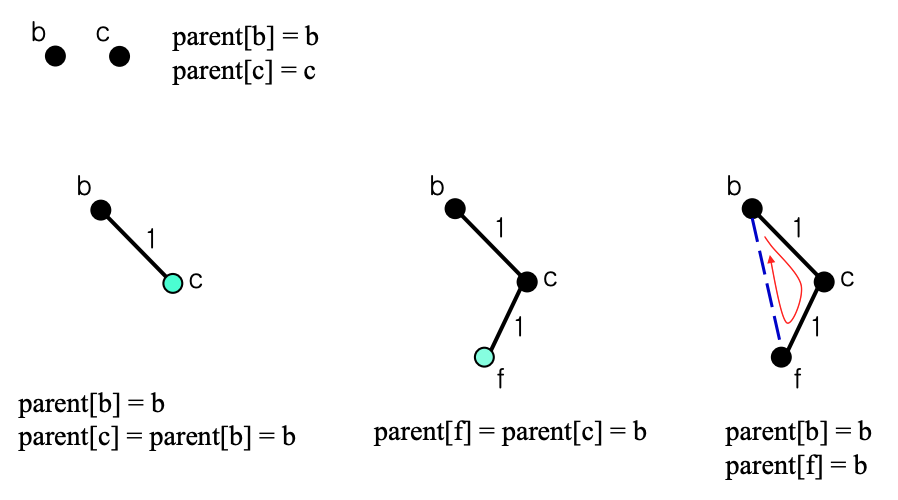
• 같은 그룹은 어떻게 판별해내는가?
  - 각 그룹마다 대표(parent)를 선정한다.

  • a,d,e의 대표는 a
  • b,c,f의 대표는 b
  • parent[d] = a != b = parent[b]
  • parent[b] = b = b = parent[f]

시간 복잡도

1. Line 1: 간선 정렬 => $O(nlogn)$
2. Line 2: 최소 신장 트리 T 초기화 => $O(1)$
3. Line 3~8: while 루프 수행, while 루프 내에 간선 e가 사이클을 만드는지 검사하는데 걸리는 시간 $O(loglogm)$ 시간

$O(mlogm)$ 소요