Prim MST Algorithm

Prim MST Algorithm

• 주어진 가중치 그래프에서 임의의 점 하나를 선택한 후, (n-1)개의 간선을 하나씩 추가시켜 트리를 생성
• Kruskal의 경우 간선의 비용을 항상 최소로 정했다면 Prim 알고리즘의 경우 정점을 기준으로 항상 최소의 가중치를 추가하여 트리를 증가하는 'Greedy'한 방법

Peseudo Code

PrimMST(G)
입력: 가중치 그래프 G=(V,E), |V|=n, |E|=m
출력: 최소 신장 트리 T

1. G에서 임의의 점 p를 시작점으로 선택 D[p] = 0
	//여기서 D는 T에 있는 u와 v를 연결하는 간선의 최소 가중치를 저장하기 위한 원소
2. for(점 p가 아닌 각 점 v에 대하여) {
3.	if (간선 (p,v)가 그래프에 있으면
4.    	D[v] = 간선 (p,v)의 가중치
5.    else
6.    	D[v] = inf
	}
7.    T = {p}
8.    while (T에 있는 점의 수 < n) {
9.    	T에 속하지 않은 각 점 v에 대하여 D[v]가 최소인 점 
		Vmin과 연결된 간선 (u,Vmin)을 T에 추가, 
        여기서 U는 T에 속한 점이고, 점 Vmin도 T에 추가
10.		for (T에 속하지 않은 각 점 w에 대해서) {
11.			if(간선 (Vmin,w)의 가중치 < D[w])
12.				D[w] = 간선 (Vmin,w)의 가중치 --> D[w]를 갱신
			}
        }
13.	return T

D[v] 추가 내용

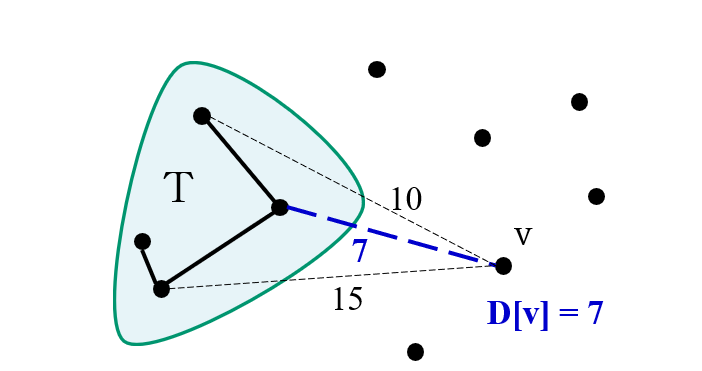
• D[v]는 점 v와 T에 속한 점들을 연결하는 간선들 중에서 최소 가중치를 가진 간선의 가중치를 저장함
• 아래의 예제에서는 최소 가중치인 7이 저장된다.
  

알고리즘 수행 과정

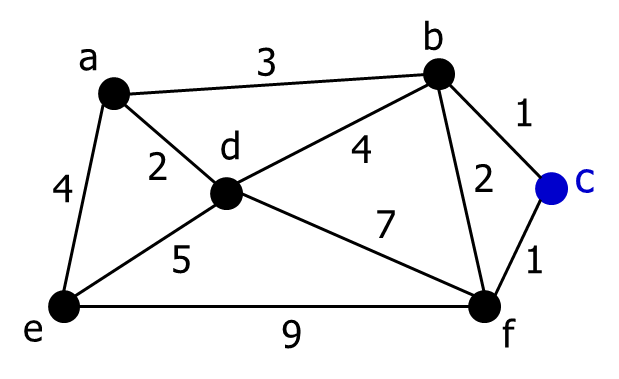
• 가장 먼저 임의의 점 C를 선택하고, D[c]=0으로 초기화한다.

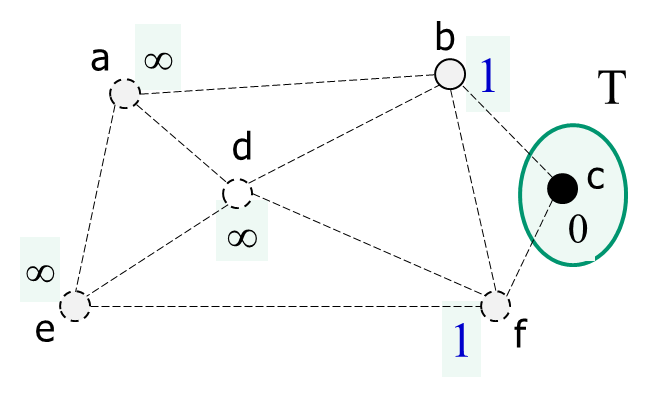
• 그리고 연결된 점 b,f를 각 간선의 가중치인 1로 초기화한다.
• 비인접 점들은 전부 inf로 초기화한다.

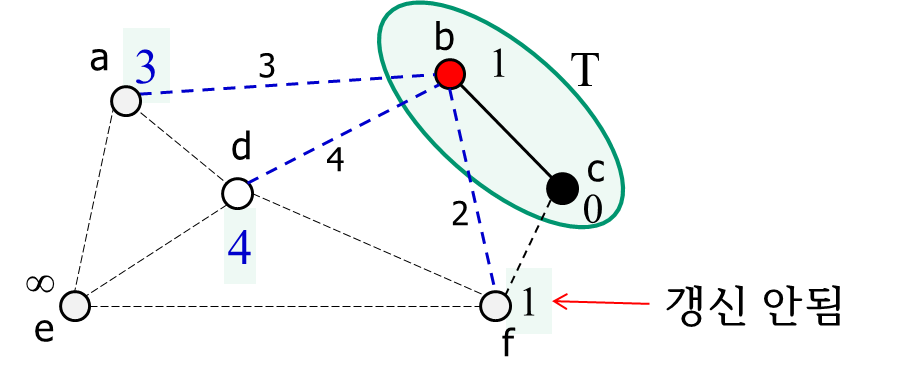
• 위와 같이 최단 가중치로 지속적으로 갱신해준다.

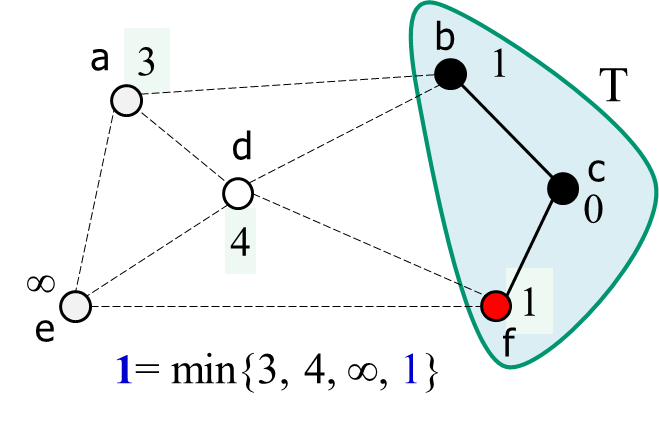
• 그리고 가장 낮은 가중치인 f와 인접한 정점의 가중치를 갱신한다.
• 그리고 가장 낮은 비용의 간선을 연결한다.
• 이 과정을 최소신장트리가 완성될 때 까지 반복

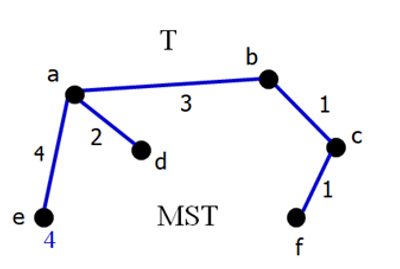
사이클이 만들어지지 않는 이유?

• 프림 알고리즘은 항상 mst를 만들고 거기에 점을 추가하는 작업을 실행하기 때문에 사이클이 만들어지지 않는다.

시간 복잡도

• while-루프가 $(n-1)$회 반복되고,
• 1회 반복될 때 line 9에서 T에 속하지 않은 각 점 $V$에 대하여, $D[V]$가 최소인 점 $V_{min}$을 찾는데 $O(n)$ 시간 소요
• 배열 D에서 최솟값을 찾고 배열의 크기는 $n$이기 때문
• 따라서 $O(n^2)$이 걸리나, 최소 힙을 사용하면 $O(mlogn)$ 간선 수가 $O(n)$이면 $O(nlogn)$이다.