0. 들어가며
지난 포스팅에서는 Logistic Regression Model에 대해서 알아보았다.
이번 포스팅에서는 Artificial Neural Network 즉, Neural Network Model에 대해서 알아볼 예정이다.
1. 뉴럴네트워크 모델 배경
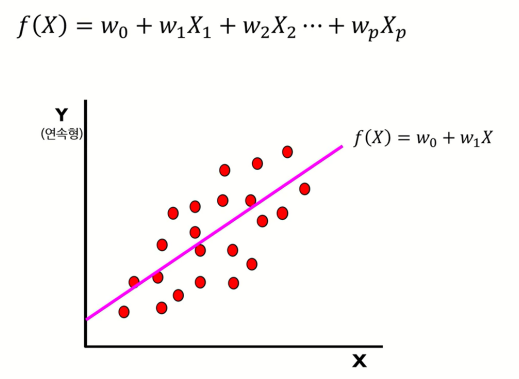
Linear Regression Model에서는 출력변수 Y가 연속형인 경우, 입력변수 X의 선형결합으로 출력변수 Y를 표현하였다.
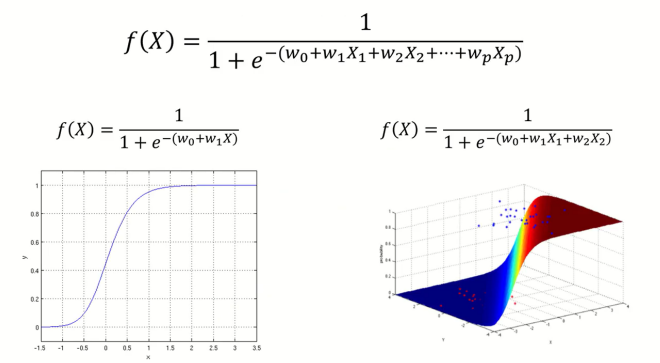
Logistic Regression Model에서는 출력변수 Y가 범주형인 경우, 입력변수 X의 비선형결합(Logistic function)으로 출력변수 Y를 표현하였다.
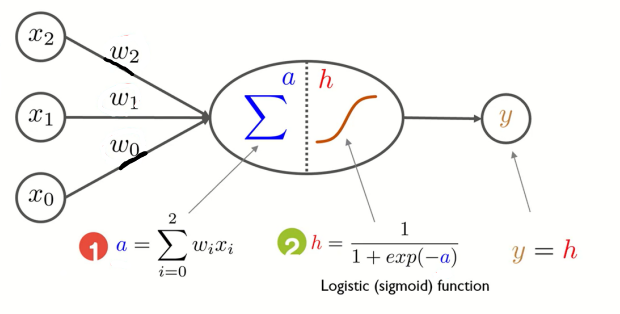
오늘 배울 Neural Network Model에서는 위처럼 일종의 신경망 구조로 출력변수 Y를 표현한다.
각 단계에서의 과정은 다음과 같다.
- 각각의 입력과 가중치를 선형결합한 값을 a에 저장한다
- 1번 과정에서 얻은 a를 Sigmoid function의 입력값으로 넣고, 그 값을 h에 저장한다
- 2번 과정에서 얻은 h를 출력 y로 내보낸다
1. 퍼셉트론(Perceptron)
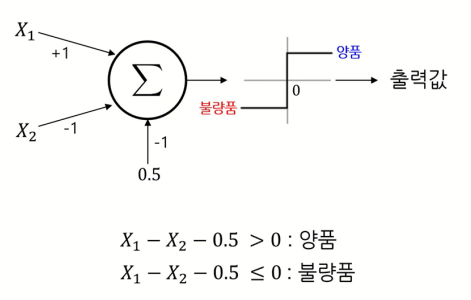
초기의 Neural Network는 퍼셉트론(Perceptron)이라고 불리우고 위와 같다.
보이는 바와 같이 하나의 신경망으로 이루어진 단층 퍼셉트론이고, 입력값의 선형결합 값을 구하고 그 값이 0보다 큰지를 여부로 분류하는 모델이었다.
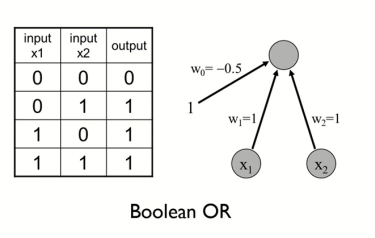
이러한 단층 퍼셉트론으로 위와 같은 OR gate나
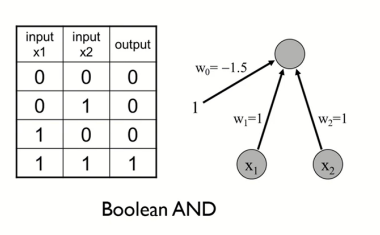
위와 같은 AND gate를 표현할 수 있었다.
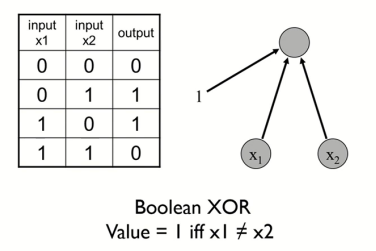
그러나, XOR gate와 같은 모델은 단층 퍼셉트론만으로 표현할 수는 없다는 단점이 존재했다.
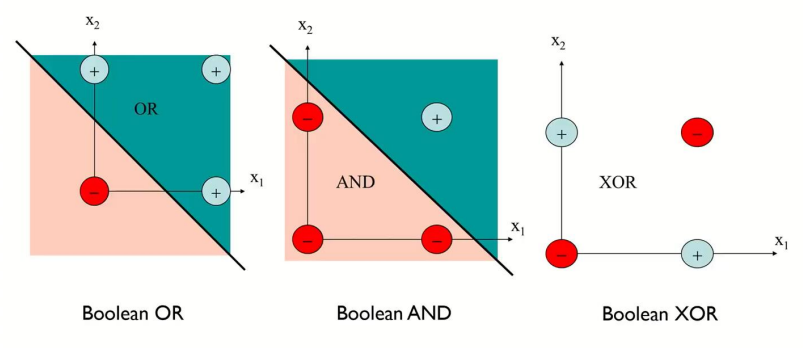
그 이유는, 단층 퍼셉트론은 하나의 선형결합으로 표현된 직선이기에 위처럼 XOR gate를 하나의 직선으로 구분할 순 없기 때문이다.
2. 2중 퍼셉트론(2-layer Perceptron)
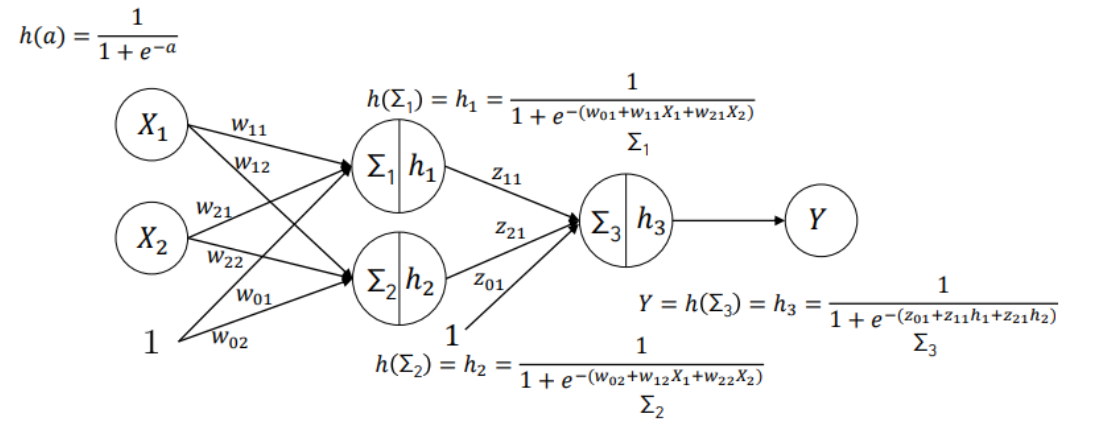
그래서 새로 고안된 모델이 위와 같은 2중 퍼셉트론(2-layer perceptron)이다.
2중 퍼셉트론은 입력변수와 출력변수 사이의 layer를 단층 퍼셉트론에서 하나 더 추가한 모델이다.
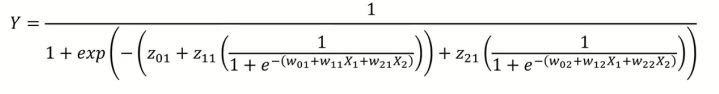
위 모델의 식을 정리하면 출력변수 Y는 위처럼 나타낼 수 있다.
3. 다층 퍼셉트론(Multilayer Perceptron)
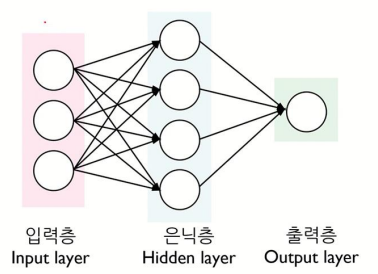
여러개의 층을 가지는 퍼셉트론을 다층 퍼셉트론이라고 부르는데, 다층퍼셉트론은 입력층, 은닉층, 출력층으로 구성된다.
- 입력층 (Input layer)
- 입력 변수의 값이 들어오는 곳
- 입력 변수의 수 = 입력 노드의 수
- 은닉층 (Hidden layer)
- 은닉층에는 다수의 노드 포함 가능
- 다수의 은닉층 형성 가능
- 출력층 (Output layer)
- 범주형 출력 노드의 수 = 출력 변수의 범주 개수
- 연속형 출력 노드의 수 = 출력 변수의 개수

지금까지 배웠던 모든 모델의 식을 모두 정리하면 위와 같다.
2. 뉴럴네트워크 파라미터
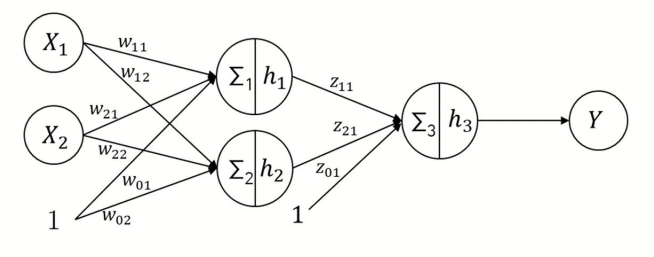
Neural Network Model에서는 parameter와 hyper-paramter가 각각 존재한다.
-
parameter
가중치 w11, w12, ... , z11
-> 알고리즘으로 결정 -
hyper-parameter
은닉층 개수, 은닉노드 개수, activation function 종류
-> 사용자가 임의로 결정
3. Activation Function (활성화 함수)
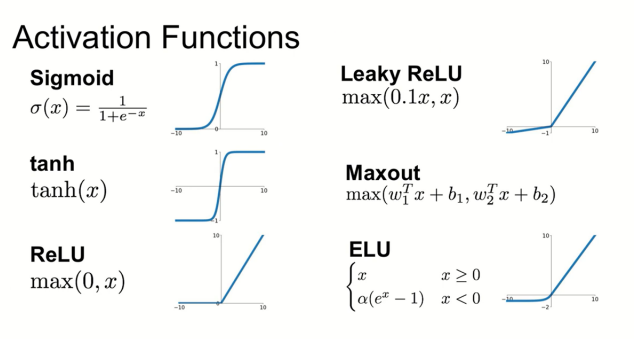
Activation function으로는 일반적으로 위에 나와있는 함수를 주로 사용한다.
이때, activation function 중 sigmoid function이 있는 것을 확인할 수 있다.
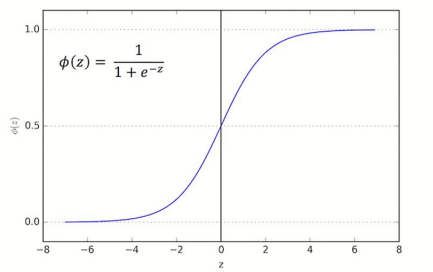
sigmoid function은 Logistic Regression Model에서도 말했듯이 위와 같은 개형을 가지고, 여러 가지 주요 특징이 있다. 자세한 내용은 이전 내용을 다시 보고 오기를 바란다.
4. 비용함수
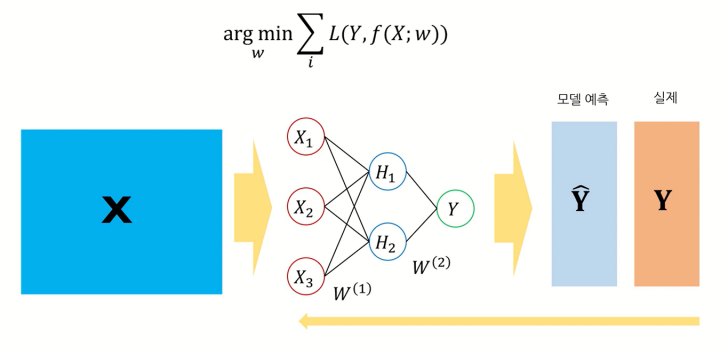
Neural Network Model도 Linear Regression Model이나 Logistic Regression Model처럼 예측값과 실제값의 차이를 최소로 하는 가중치 w를 찾는 과정을 거치면 된다.
또한 Linear Regression Model은 출력변수 Y가 연속형인 경우에만, Logistic Regression Model은 출력변수 Y가 범주형인 경우에만 사용할 수 있었던 반면, Neural Network Model은 모두 사용할 수 있다.
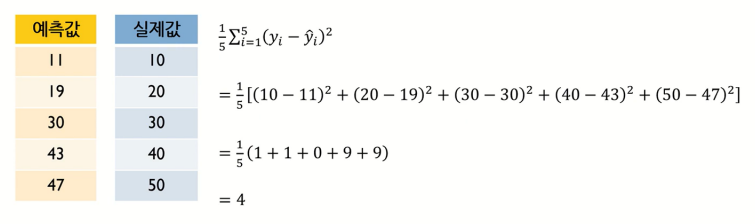
만약 출력변수 Y가 연속형인 경우에는 Linear Regression Model에서 그랬듯이 cost function을 MSE로 하여 사용하면 된다.
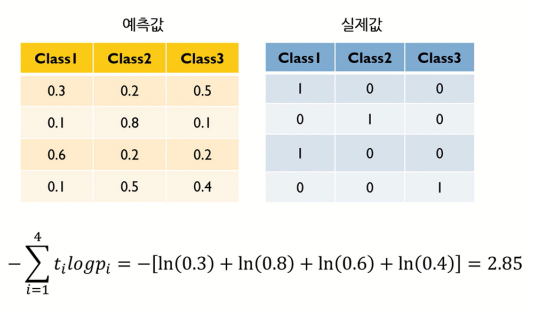
출력변수 Y가 범주형인 경우에는 Logistic Regression Model에서 그랬듯이 cost function을 MLE 혹은 cross entropy를 사용하면 된다.
5. 뉴럴네트워크 학습 - 경사하강법
비용함수를 정의했다면 이제 어떤 방식으로 비용함수가 최소가 되는 가중치 w를 찾을 것인지 알아야 한다.
Neural Network Model에서는 경사하강법(Gradient Descent Method)이라는 방법을 사용하여 최적의 가중치 w값을 찾아낸다.
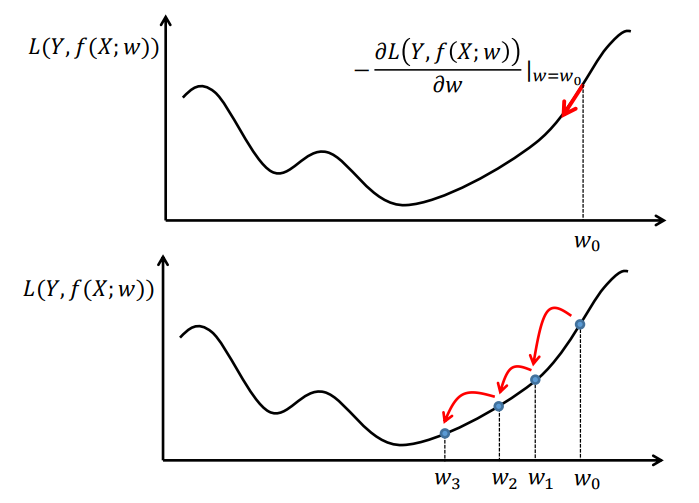
경사하강법(Gradient Descent Method)은 비용함수(Loss function)를 미분하여 0이 되는 w값을 찾아내는 과정이다.
Loss function이 최소가 되는 지점은 미분했을 때의 기울기가 0인 지점과 일치할 가능성이 높을 것이다.
따라서 Loss function을 미분하고, 미분하여 0이 되는 w값을 계속해서 update하면서 최소가 되는 지점을 찾아야 한다.
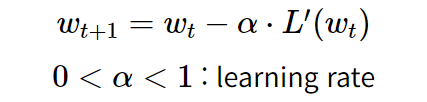
w를 update하는 식은 위와 같다. 여기서 α는 learning rate로 학습률을 의미하고, 0과 1사이의 값이다.
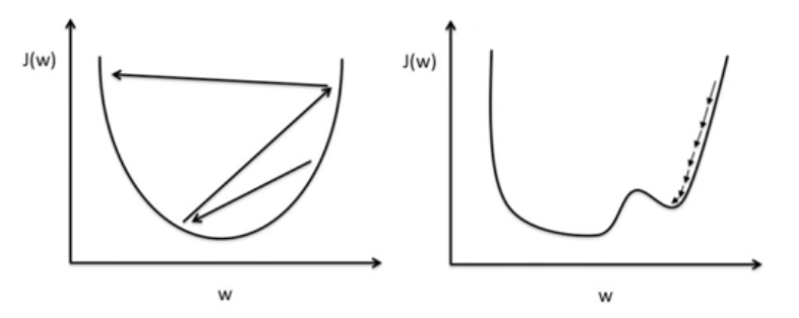
(왼쪽 그림)
만약 α값을 크게 설정한다면 step size가 크기 때문에 최적화된 w값을 지나쳐 학습이 이루어지지 않고, 오버슈팅이 일어날 수도 있다.
(오른쪽 그림)
반대로 α값을 작게 설정한다면 step size가 작기 때문에 훈련 시간이 길어져서 학습의 성능이 떨어지거나, local minima에 빠져 최적화된 w값을 찾기 전에 학습이 끝날 수도 있다.
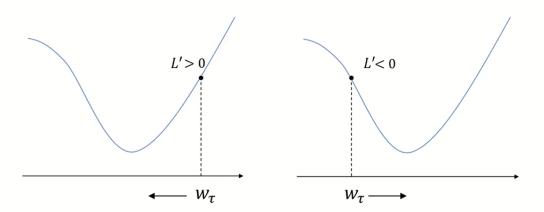
만약 L'값이 양수라면 가중치 w는 왼쪽 방향으로 update하면서 학습을 진행하게 될 것이고,
L'값이 음수라면 가중치 w는 오른쪽 방향으로 update하면서 학습을 진행하게 될 것이다.
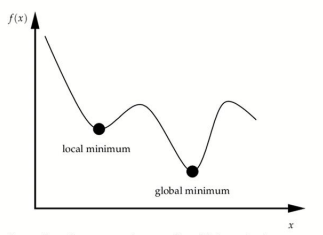
이러한 Gradient Descent Method는 학습을 진행하면서 모든 구간에서 Loss function이 가장 작은 지점을 찾을 수도 있는 반면, 일정 구간에서만 Loss function이 가장 작은 지점을 찾을 수도 있다.
각각의 지점을 Global minimum, Local minimum이라고 한다.
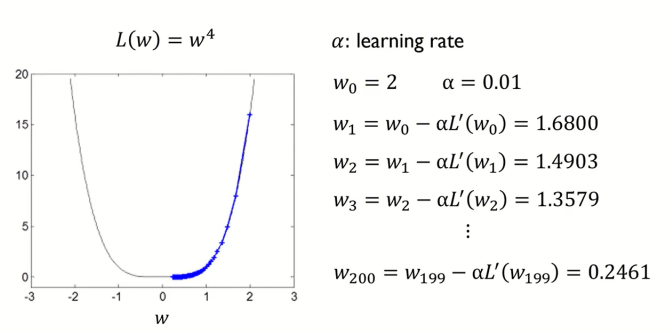
실제 예제를 보면서 Gradient Descent Method 방법을 익혀보자면 위와 같다.
초기 가중치 w0을 2로, learning rate α를 0.01로 설정하고, 경사하강법을 진행하면 가중치 w값이 업데이트가 되면서 Loss function이 최소가 되는 w지점으로 값이 update 되는 것을 확인할 수 있다.
6. 마치며
오늘은 Neural Network Model의 간단한 개요와 경사하강법(Gradient Descent Method)에 대하여 알아보았다.
또한 필자는 고려대학교 김성범 교수님이 운영하시는 유튜브 채널을 보고 공부한 내용을 포스팅 하였으므로 아래 출처를 남긴다.
https://www.youtube.com/@user-yu5qs4ct2b
