1. 통계
통계(Statics)는 데이터의 수집, 분석, 추론, 요약 등의 방법론을 다룬다.
통계에서 주로 등장하는 용어들이 있는데 이는 아래와 같다.
-
모집단(Population)
통계학에서 관심/조사의 대상이 되는 개체의 전체집합 -
모수(Parameter)
모집단에 대한 수치적 요약 -
표본(Sample)
모집단을 적절히 대표하는 모집단의 일부 -
통계량(Statistic)
표본에 대한 수치적 요약
즉, Population과 Paramter가 한 쌍이고, Sample과 Statistic가 한 쌍이다.
2. 자료의 종류
범주형 자료: 속성의 범주화, 상대적 서열도 표현- 명목형 자료: 단순히 속성을 분류하기 위함 (혈액형)
- 순서형 자료: 상대적인 크기의 비교 (만족도, 최종학력)
양적 자료: 자료자체가 숫자로 표현됨- 이산형 자료: 셀 수 있는 자료 (빈도수, 불량품의 수)
- 연속형 자료: 셀 수 없는 자료 (길이, 시간)
3-1. 통계량 - 중심
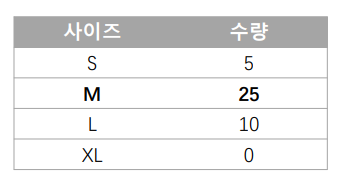
최빈값 (mode)- 발생빈도가 가장 높은 값
- 극단값에 영향을 받지 않음
- 주로 범주형 자료에 대한 대표값
- 2개 이상 존재 가능

중앙값 (median)- 크기 순으로 정렬된 자료에서 가운데에 위치하는 값
- 관측값 변화에 민감하지 않음
- 극단값에 영향을 받지 않음
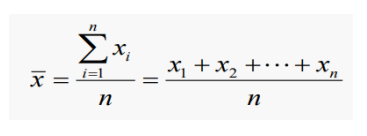
산술평균 (Arithmetic Mean)- 모든 자료의 값을 더하여 자료의 수로 나누어 준 값
- 모든 값을 반영하므로 극단값에 영향을 받음
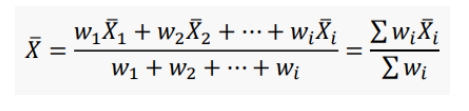
가중평균 (Weighted Mean)- 자료의 중요성이 각기 다를 경우 중요도에 따라 가중치를 부여한 평균
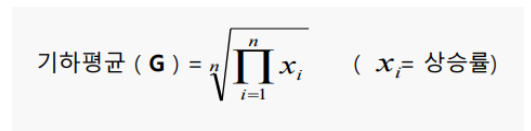
기하평균 (Geometric Mean)- 자료가 성장률, 증가율 등 앞 시점에 대한 비율로 나타난 경우 유용한 통계량
- 음수가 아닌 자료값만 사용 가능
- ex) 연간 물가 상승률, 일일 주가 상승률 등
3-2 통계량 - 산포
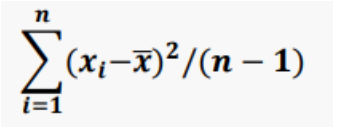
분산 (Variance)- 편차 제곱의 합을 자료의 수로 나눈 값
- 편차 제곱의 평균값
- 편차 제곱을 하는 이유는 편차의 합은 0으로 나오기 때문
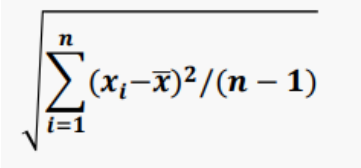
표준편차 (Standard Deviation)- 분산을 제곱근한 값
- 제곱근을 취하는 이유는 분산에서 제곱연산으로 인하여 up-scale 된 것을 다시 down-scale 하기 위함
3-3 통계량 - 형태
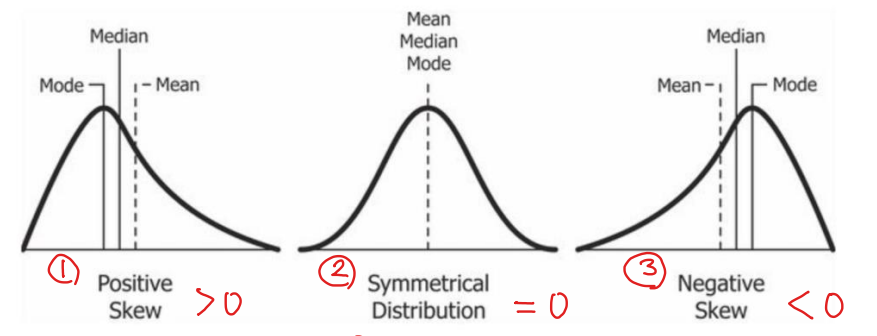
왜도 (Skewness)- 분포의 비대칭도

첨도 (Kurtosis)- 뾰족한 정도
- 표준정규분포의 첨도는 3
3-4 통계량 - 상관
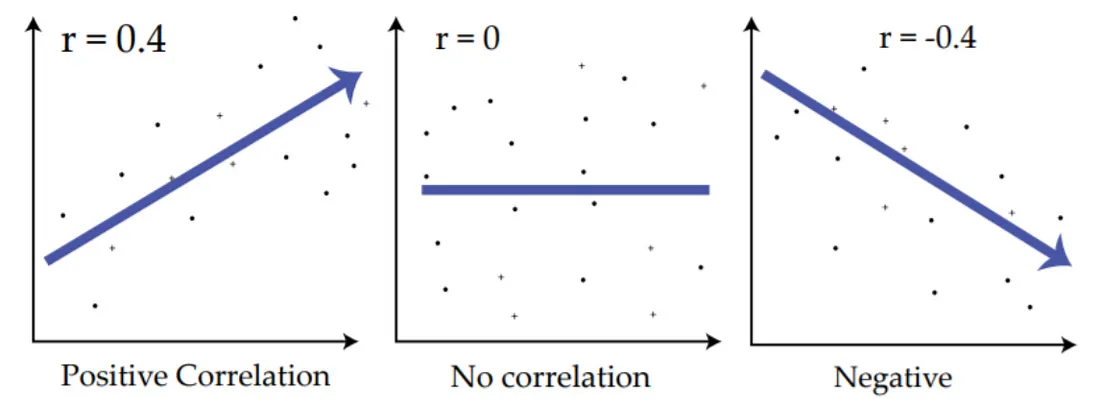
상관 (Correlation)- 확률변수 X, Y의 변화가 서로 관계가 있을 때 상관관계가 있다고 함
- 선형적 관련성을 파악할 수 있음
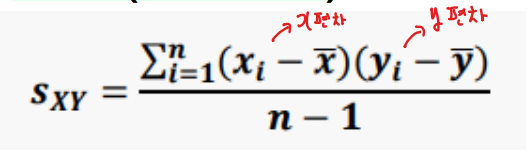
공분산 (Covariance)- X편차와 Y편차의 곲한 값의 합을 자료의 수로 나눈 값
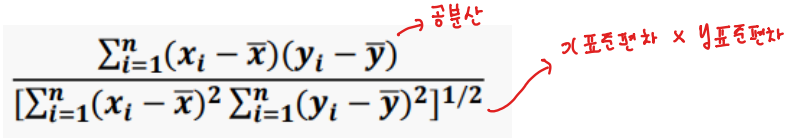
상관계수 (Correlation Coefficient)- 공분산을 두 변수의 표준편차의 곲으로 나눈 값
- -1 < r < 1
- 두 양적 변수 간의 선형적 연관성의 강도 측정
- 단위가 없음
- 절댓값이 1에 가까울 수록 연관성의 강도가 높음
4. 마치며
오늘은 통계에서의 기본적인 내용들을 조금 알아보았다.
다음 포스팅에서 나머지 내용을 계속 이어나가겠다.
또한, 본 포스팅은 유튜브 메타코드 채널을 참고로 공부한 내용을 포스팅하였으니 아래 출처를 밝힌다.
