[ML] Bagging

9e0na·2023년 8월 21일
MachineLearningpython
1

[머신러닝]

목록 보기
5/5
post-thumbnail

주제: Bagging

1. Bagging

1.1. Ensemble이란?

  • 여러 개의 단순한 모델을 결합하여 정확한 모델을 만드는 방법
  • '정확도가 높은 강한 모델을 하나 사용하는 것보다, 정확도가 낮은 약한 모델을 여러개 조합하는 방식의 정확도가 높을것'이라는 Idea
  • Bagging, Boosting, Voting, Stacking 등이 있음.

1.2. Bagging이란?

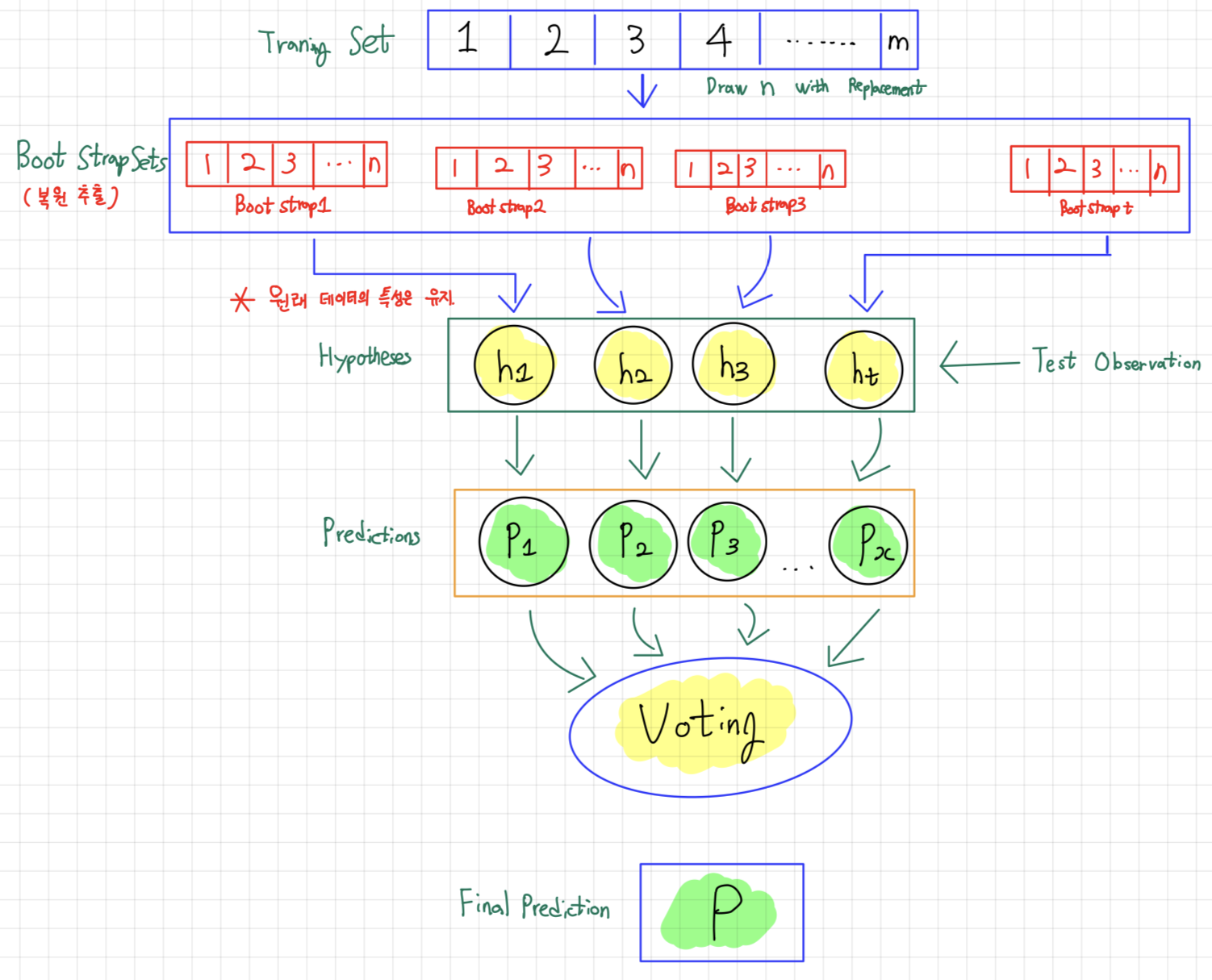
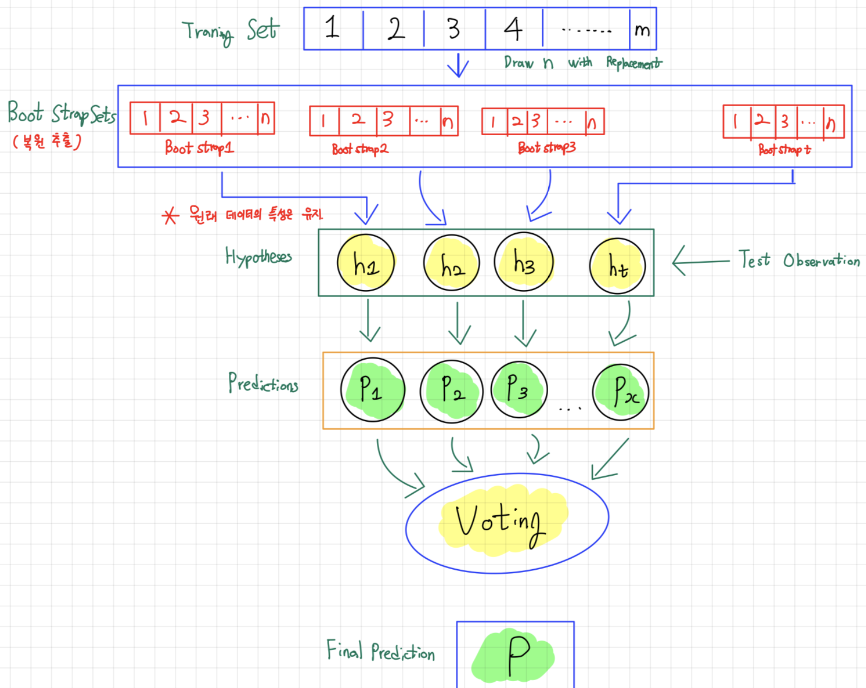
  • Bootstrap Aggregating으로, sample을 여러번 뽑아(Bootstrap = 복원 랜덤 샘플링) 각 모델을 학습시켜 결과물을 집계 (Aggregation)하는 방법임.
  • 각 모델별로 기존 데이터 셋에서 중복을 허용하고 무작위로 N개의 Feature를 선택한 후, 선택한 Feature를 통해 만들어진 각 모델의 결과를 취합하는 방법.
    -> 각 모델은 서로 독립적임
  • Bagging 방식으로 만들어진 Ensemble model은 각 모델들의 결과를 취합하여 분류일 경우 voting(투표), 회귀일 경우, 평균값으로 결과 도출.
  • 대표적인 기법: Random Forest

1.3. Bagging의 Bootstrap

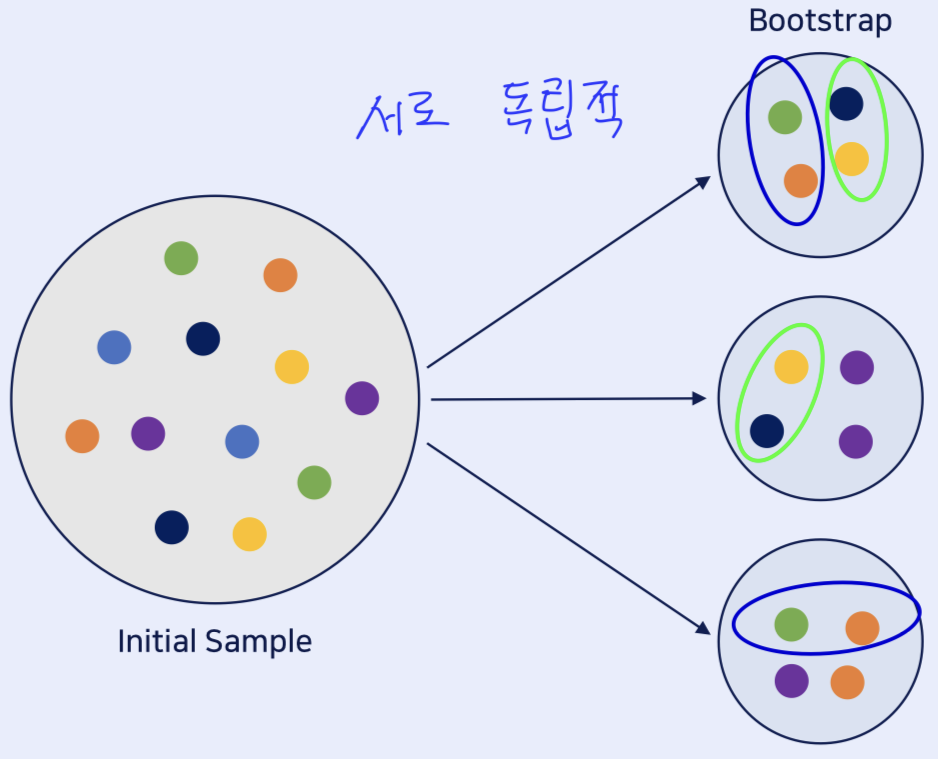
  • 위의 그림과 같이 어떤 sample은 여러 번 또는 전혀 선택되지 않을 수도 있음.
    -> 이때 한번도 선택되지 않은 sample은 oob(out-of-bag)

💌 Bagging에서 oob sample은 Training 사용 XX

  • oob sample을 사용하여 모델 평가 가능
  • Ensemble의 평가는 각 예측기의 oob 평가를 평균하여 얻게 됨.

1.4. Bagging의 한계점

  • 각 dicision node를 분리할 때 모든 Feature를 고려해서 Error를 계산함.
    -> Decision Tree에서 node를 분리할 때 모든 feature의 정보 이득을 계산한 이후, 정보 이득이 높은 feature를 기준으로 분리함.
  • 각 sub sample을 구성할 때 복원 추출하기 때문에 sample의 특성이 유사함.
    -> 보통 모집단의 1/31/3 정도가 oob가 됨.

2. Random Forest

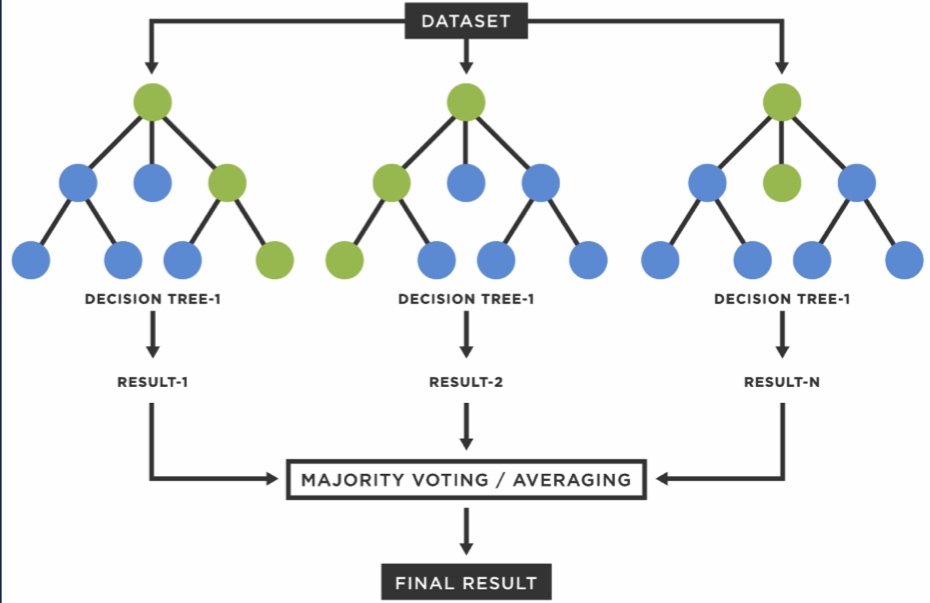
  • 수많은 Decision Tree가 합쳐져 만들어진 Ensemble Model임.
  • 여러개의 Decision Tree가 생성되고, 각 Model은 각자의 방식으로 데이터를 sampling하여 개별적으로 학습 진행.
    -> 분류일 경우 voting(투표), 회귀일 경우, 평균값으로 결과 도출.
  • Breiman이 2001년에 개발
  • 데이터의 2/32/3만 사용하고 나머지 1/31/3은 테스트 세트로 사용함.

2.1. 장점 & 단점

장점

  • 분류와 회귀에 모두 사용 가능함.
  • 대용량 처리에 효과적이고, decision tree의 훈련데이터에 overfitting 되는 단점 해결가능.
    -> 다수의 나무를 기반으로 예측하기 때문에 각 분류기의 영향력이 줄어들게 되어 좋은 일반화 성능을 보임.
  • 전체 학습용 데이터에서 무작위로 복원 추출된 데이터를 사용함으로써 잡음이나 outlier로부터 크게 영향 X
  • 분석가가 feature 선정으로부터 자유로워짐.
  • class의 빈도가 불균형일 경우 타 기법에 비해 우수한 예측력을 보임.

*# Version 1.1 이후 각 Decision Tree에서 node를 분할할 때 모든 Feature가 아닌 random하게 일부의 feature만을 사용함.

단점

  1. 최종 결과에 대한 해석이 어려움
    -> 시각화를 통한 해석을 위해서는 단일 의사결정나무 사용

  2. 대량의 데이터를 분석할 경우 상당한 시간 소요
    -> 멀티 코어 CPU인 경우 scikit-learn에서는 n_jobs 파라미터를 이용하여 병렬처리 가능

  3. Feature 차원이 높고 sparse한 데이터에는 작동 X
    -> 선형 모형이 더 적합함.

2.2. Algorithm

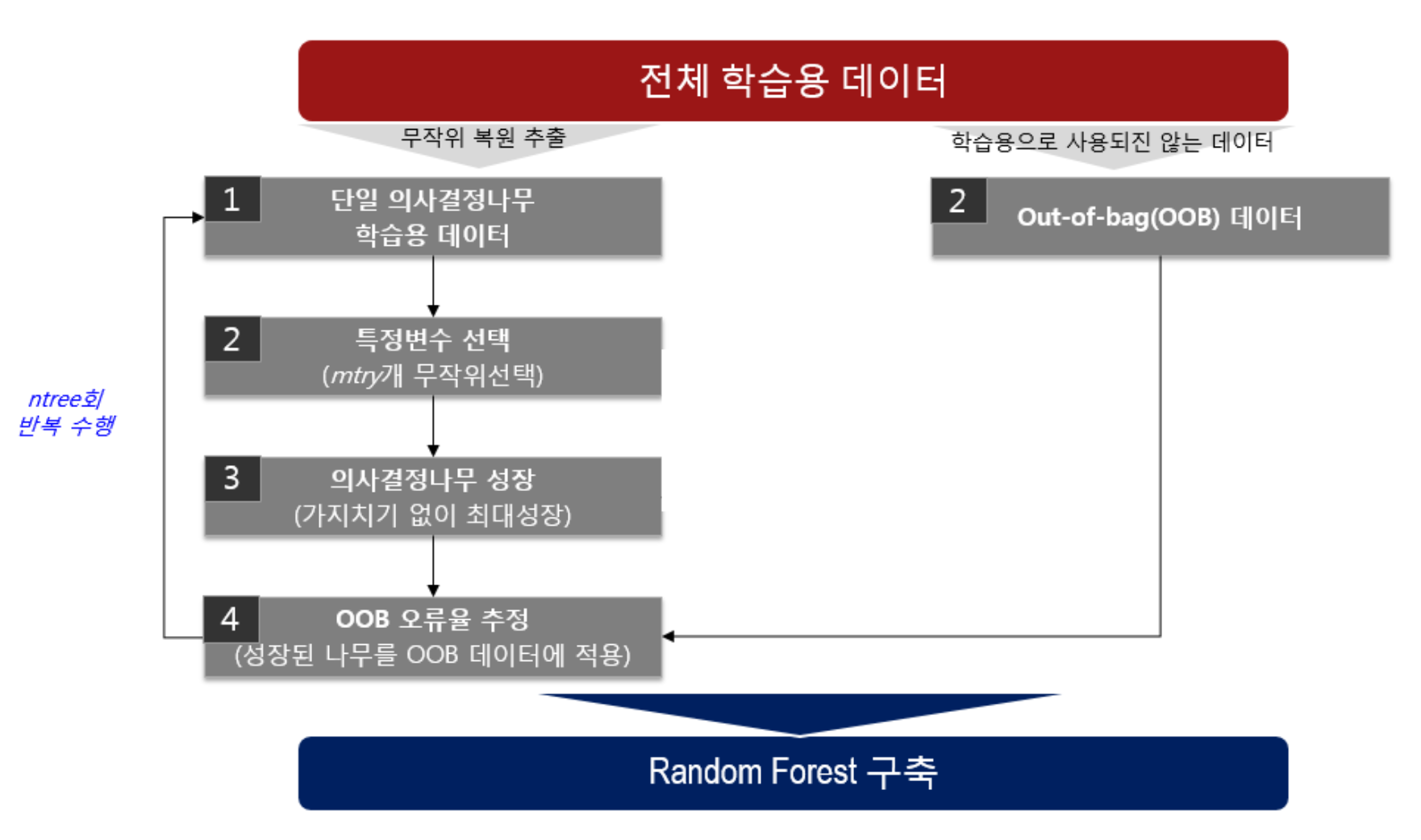
1. Random Forest에 적용될 기본 모수에 대한 값을 정함.

  • ntree
    🤜 RF를 구성할 때 전체 의사결정나무의 개수를 의미
    🤜 대수의 효과를 얻을 수 있도록 큰 상수 값으로 설정하며, Default값은 500임.
  • mtry
    🤜 RF를 구성하는 의사결정나무에서 사용될 특정변수의 개수를 의미
    🤜 전체 특징변수의 개수가 MM이라고 할 때,
    - 분류를 위한 의사결정나무: mtry = (M)\sqrt(M)
    - 예측을 위한 의사결정나무: try = M/3M/3

2. 특정 변수 선택

  • XiX_i는 전체 학습용 데이터(X)에서 단순 무작위 표본, 복원 방식으로 추출
  • 부트스트랩 표본 XiX_i (ii = 부트스트랩 반복 횟수)를 추출

3. 의사결정나무 성장 (가지치기 없이 최대 성장)

  • Bootstrap 표본 XiX_i를 이용하여 이진 의사결정나무를 성장
  • 가지를 분할하기 위한 최적 분할 결정 시 무작위로 선택된 mtry개의 특정벼눗만 사용
  • 최적의 분할 시 분할 기준은 지니계수를 사용
  • 나무는 가지치기를 하지 않고 최대한 성장시킴.

4. OOB 오류를 추정 (성장된 나무를 OOB 데이터에 적용)

  • 특정변수 선택 단계에서 추출된 OOB 데이터들 앞서 구축된 의사결정나무에 적용하여 예측결과를 산출
  • 예측결과와 실제결과를 비교하여, OOB 데이터에 대한 오류율 산출

5. Random Forest 구축

  • 최종적으로 1~4 단계를 ntree회 반복하고, ntree개의 개별 의사결정나무로 구성된 RF 구성함.
  • 종속변수가 연속형인 경우: 평균
  • 종속변수가 범주형인 경우: 투표
  • mtry와 ntree의 적정성: ERRERR_OBB를 종합

2.3. 주요 파라미터

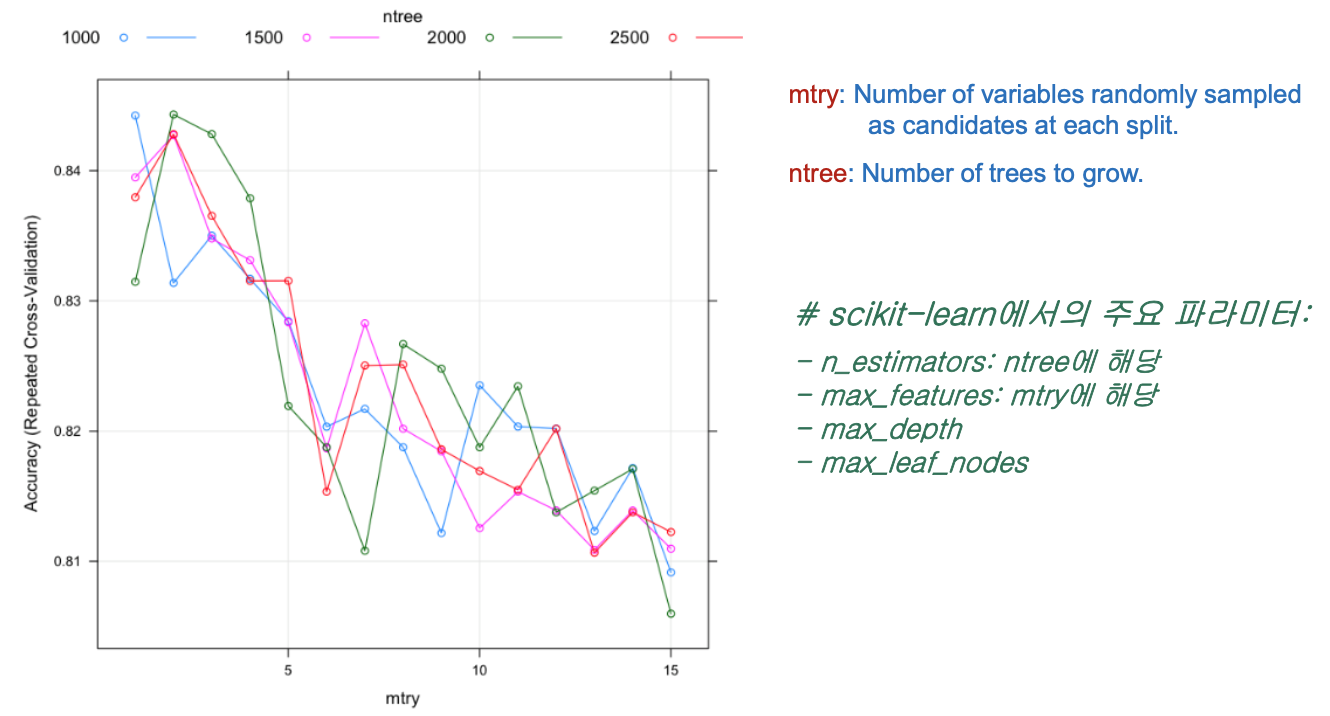
  • n_estimators: ntree 해당
  • max_features: mtry 해당
  • max_depth
  • max_leaf_nodes

3. ExtraTrees

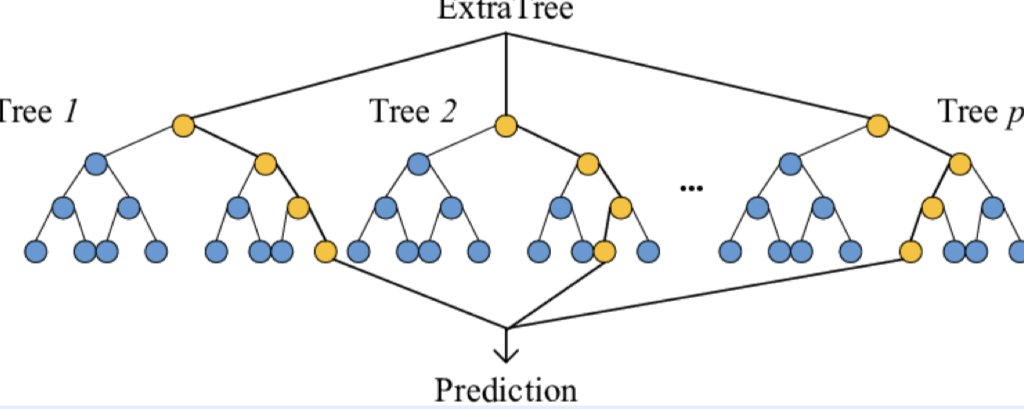
  • Random Forest와 매우 비슷하지만, 이보다 더 극단적으로 Random하게 만든 Model.
    -> 비복원 추출로 Bootstrap을 사용하지 않음
    -> Bagging XX

3.1. 장점

  • Random Forest보다 Random하기 때문에 연산량이 적고 속도가 빠름.
  • 개별 Tree의 성능은 Random Forest보다 낮지만, 많은 Tree를 Ensemble하기 때문에 overfitting을 막고 일반화 성능을 높일 수 있음.

3.2. Algorithm

  1. 무작위로 feature를 sampling 진행.
    -> 비복원 추출 사용

  2. sampling된 feature를 N개라고 할 때, 그 중 random으로 N\sqrt{N}개씩 분할.

  3. N\sqrt{N}개씩 분할된 것 중 최적의 분할 방법을 갖는 Tree를 찾기.

  4. 선택된 최적의 분할 방법에 따라 각 모델의 Tree를 생성하고 학습진행.

🎯 Summary

  • Random Forest에 대해 더 깊게 알 수 있었음.
  • Bagging의 Bootstrap에서 oob sample은 Training에서 사용 안하고, oob sample를 사용하여 모델 평가가 가능하다는 것을 알게 됨.
  • Boosting model에 대한 공부를 소망하며 오늘의 study 끝!

📚 References

  • 김성진 & 안현철, "랜덤 포레스트를 활용한 기업채권등급평가 모형", 2014.
profile
9e0na
디지털 마케터가 되기 위해 [a-zA-Z]까지 정리하는 거나입니다 😊

0개의 댓글