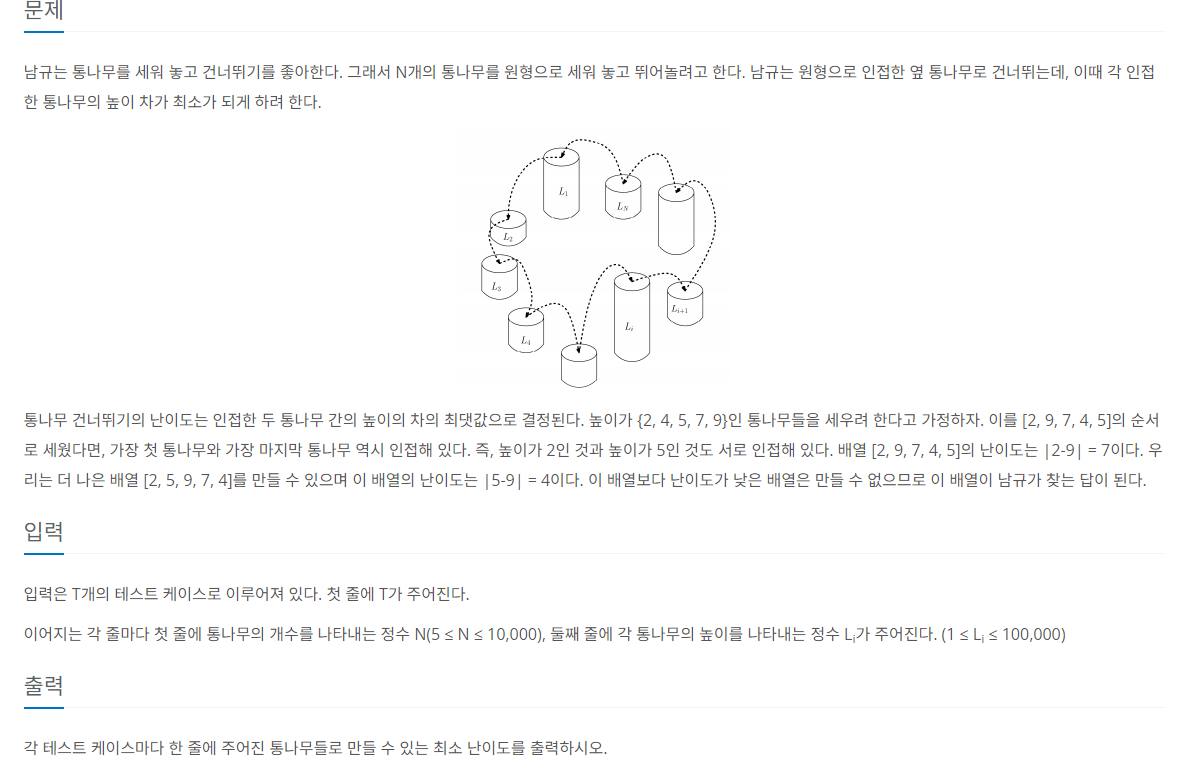
문제를 보 갈피를 못 잡았지만, 문제 유형을 확인하고 정렬과 그리디라는 힌트를 얻은 후 쉽게 도출할 수 있었다.
처음과 마지막 통나무 또한 이어진다는 가정하에 순환구조를 어떻게 표현할지 고민해야했다.
-
우선 통나무 간의 최소 높이를 구할 수 있는 가장 쉬운 방법은 입력된 통나무를 나열하는 것
-
그 후 처음 통나무부터 높이차를 순서대로 양쪽에 삽입하면 뛰는 높이 난이도가 낮은데로 배치가 가능하다.
-
꼭 숫자가 낮은 순으로 올 필요가 없기 때문에, 데크를 사용하여 논리적 순환구조를 바라보면서 뛰었을때 가장 높은 난이도를 계산만해서 도출하였음.
case 1
여기서 왼쪽과 오른쪽에 놓는 기준이 필요하였다.
- 다음에 배치해야할 통나무의 높이(Logs Height)가 왼쪽, 오른쪽과의 차를 비교
- 만일, Logs Height가 왼쪽 통나무의 차와 오른쪽 통나무의 차 중에서
- 오른쪽 통나무와의 차가 왼쪽 통나무와의 차보다 크거나 같다면 오른쪽에 삽입
- 왼쪽 통나무와의 차가 오른쪽 통나무와의 차보다 작으면 왼쪽에 삽입
이렇게 조건을 만든 이유는, 만일 차가 더 작은쪽에만 편향적으로 통나무를 배치하다보면 반대쪽(왼쪽 <-> 오른쪽)에 놓이는 통나무는 그 차가 더 높아질 것이기 때문에,
왼쪽에 놓았다면 더 큰 편차를 만들지 않기 위해서 오른쪽에 놓으면서 밸런스를 유지하기 위함
-> 그래야 오른쪽에 놓은 후 왼쪽에도 놓을 준비가 되고, 그 반대의 경우도 안정적으로 문제를 해결할 수 있겠다고 생각하였다.
코드
import java.util.*;
import java.io.*;
public class BackJoonMemo {
public static void main(String[] args) throws Exception{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
for(int i = 0; i<n; i++){
st = new StringTokenizer(br.readLine());
int logCount = Integer.parseInt(st.nextToken());
st = new StringTokenizer(br.readLine());
int[] logList = new int[logCount];
for(int j = 0; j<logCount; j++){
logList[j] = Integer.parseInt(st.nextToken());
}
// 정렬하여 높이가 최소인 순서를 우선 구하기
Arrays.sort(logList);
System.out.println(solution(logCount, logList));
}
}
public static int solution(int logCount, int[] logList){
Deque<Integer> logComb = new LinkedList<>();
// 데크를 활용하여 양쪽에 높이가 최소인 값들을 넣을 준비
logComb.add(logList[0]);
logComb.addFirst(logList[1]);
int leftDiff, rightDiff, difficulty = 0;
for(int i = 2; i< logCount; i++){
leftDiff = Math.abs(logList[i] - logComb.getFirst());
rightDiff = Math.abs(logList[i] - logComb.getLast());
// 양쪽끝의 차가 같거나 오른쪽이 더 클 경우에 오른쪽에 통나무 정렬
if(leftDiff <= rightDiff){
logComb.addLast(logList[i]);
difficulty = Math.max(difficulty, rightDiff);
}
// 왼쪽 차가 더크면 왼쪽에 통나무 정렬
else{
logComb.addFirst(logList[i]);
difficulty = Math.max(difficulty, leftDiff);
}
}
//System.out.println(logComb);
return difficulty;
}
}결과

아무래도 입력시 정수가 최대 10000개 까지 입력되는데, 여기서
- main에서 10000개를 담기 위한 배열
- solution 함수에 매개변수로 넘겨주는 배열
- 통나무 정렬을 위한 Deque 자료형
까지 해서 메모리가 꽤 크게 잡혔다.
시간 복잡도는 : 정렬 (nlogn) + 배열 순차 탐색 (O(n))으로 계산 가능하다