Supervised Learning (지도학습)
- 머신러닝의 대부분이 지도학습으로 이루어진다.
- 데이터에 대한 정답(lable)을 알고 있어야 한다.
|선형 모델
연속형 데이터: measure (몸무게, 키, 혈당)
이산형 데이터: count (하루 당 은행 방문자 수, 사고 건 수)
범주형 데이터: category (Yes/No, Male/Female, Good/Normal/bad)
| 분류(classification) | 회귀(regression) |
|---|---|
| target(y)가 범주형 변수일 때 사용 | target(y)가 연속형, 실수형일 때 사용(count 안됨) |
머신러닝을 배우다보면 X와 Y값을 다양한 용어로 부르는 것을 알 수 있다.
헷갈리므로 다음과 같은 용어를 이용하여 개념을 정리하겠다.
| X | Y |
|---|---|
| predictor variables | predicted variable |
| independent variables | dependent variable |
| target variable | |
| class variable |
variable = feature
|비선형 모델
데이터에 계속 질문하는 모델
여기서 모델 = 알고리즘
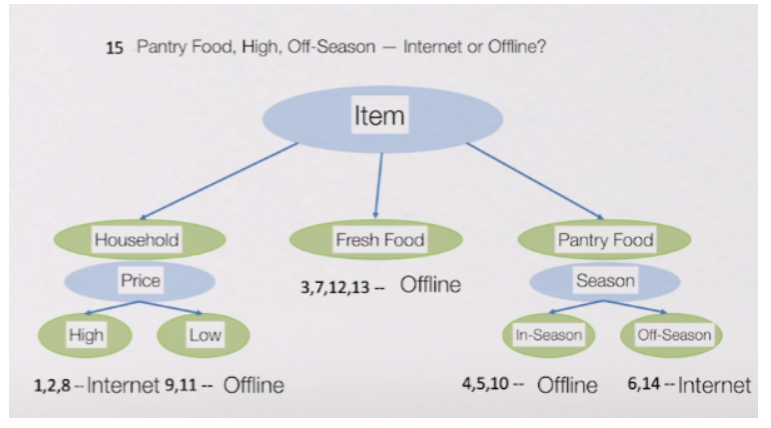
decision tree의 경우: 물건 구매 시 온라인으로 살 것인가? -> 높은 가격을 살 것인가? -> 식품을 살 것인가? -> ...
꼬리를 물고 결정 가지수를 생성한다.
지도학습 알고리즘
물론 수많은 지도학습 알고리즘 중 일부만 다룬다.
1) Decision Tree
for classification
특정 기준에 따라 데이터를 구분하는 것
특정 기준? 속성의 타입 ex. Household/Fresh Food/Pantry food
| 2-way split | multi-way split |
|---|---|
| 이진화 | 선분류 필요 |
과정
- Gini index 구하기
지니 = 불확실성, 값이 0이면 같은 특성을 가진 개체끼리 잘 모았다는 뜻 - Weighted Gini 작은 값을 split으로 택해서 노드 분류 반복
- Gini Gain 계산 클수록 이전보다 개선되었다는 뜻
장점
- 정확도 높은 편이다.
- 연속적이고 카테고리형 변수를 다루기 쉽다.
- 분류와 회귀에 둘 다 쓰일 수 있다.
단점
- 속성값이 이진값(binary)이 아니라 여러 개일 경우 정확도 감소한다.
- 학습시간이 길다.
- best split을 결정하고 나머지는 다 버린다.
2) decision tree regression
for regression
Gini대신 Standard deviation 사용 -> SDR
가장 큰 SDR을 찾는게 목표
SDR(T, X) = S(T) - S(T, X)
decision tree pruning (가지치기)
학습 모델에 도움이 되지 않는 subtrees버리는 것
계산 비용을 제한하고 overfitting을 해결할 수 있다. (Cost Function 챕터에서 자세히 설명한다.)
(노드가 23개 이상이면 정확도가 점점 감소하므로)
pre-pruning: 학습모델을 만드는 과정에서 일부 배제
post-pruning: 만들어진 후 일부 배제(bottom up or top down)
3) Logistic Regression
for regression
Simple Linear Regression y = a + bx
Multiple Linear Regerssion y = a + b1x1 + b2x2 + b3x3 ...
한개의 x를 유닛으로 나머지 x는 고정시켜서 유닛에 따라 y값이 얼마나 변하는지 구할 수 있다.
Logistic Regression
선형회귀의 변형, y가 이진 데이터일 때 사용된다. (Yes/No, Success or Fail) X는 이진, 범주형, 연속형 데이터
독립-종속 관계가 선형이 아니다.
X단위 변화량에 대한 로그 확률의 변화로 Y값을 해석한다.
logit = ln(odds)
| Y | a(target) | b |
|---|---|---|
| 확률 | 0.2 | 0.4 |
| odds | 0.2/0.8 = 0.25 | 0.4/0.6 = 0.6 |
| odd ratio | 0.25/0.6 = 0.417 |
Multiple Logistic Regression
독립변수 두 개 이상 -> 손으로 계산 불가능 -> 통계 소프트웨어(R)을 통해 구함.
SSE(Sum of Squared Error) - 낮을수록 좋다
TSS(Total SUm of Squared) - 낮을수록 좋다
R2(coefficient of determination) - 1에 가까울수록 좋다.
4) SVM (Support Vector Machine)
for classification & regression
비확률적 이진분류기.
주어진 데이터가 어떤 카테고리에 속할지 분석
회귀, 아웃라이어 분석, 순위 매기기 등에 맞게 조정되었다.
SVM 은 기준선을 구할 때 전체 데이터셋이 아닌 서포트 벡터를 이용한다.
서포트 벡터 - 기준선에 가장 근접한 양 측 점
2d: separating line
3d: separating plane
nd: separating hyperplane
깔끔하게 분리하기 어려운 경우가 대부분
<1> Soft Margin
Hard Margin의 조건을 완화한 wide margin.
넓은 여백으로 일부 예상 오류를 수용한다.
penalty parameter C - 높은 값일수록 margin을 생성하는 데이터를 허용하지 않는다는 의미 (Cost Function 챕터에서 자세히 설명한다.)
최적의 C값은 시행착오를 통해 도출한다.
C = 1/margin
n개의 속성을 가진 데이터에는 최소 n+1개의 서포트 벡터가 필요하다.
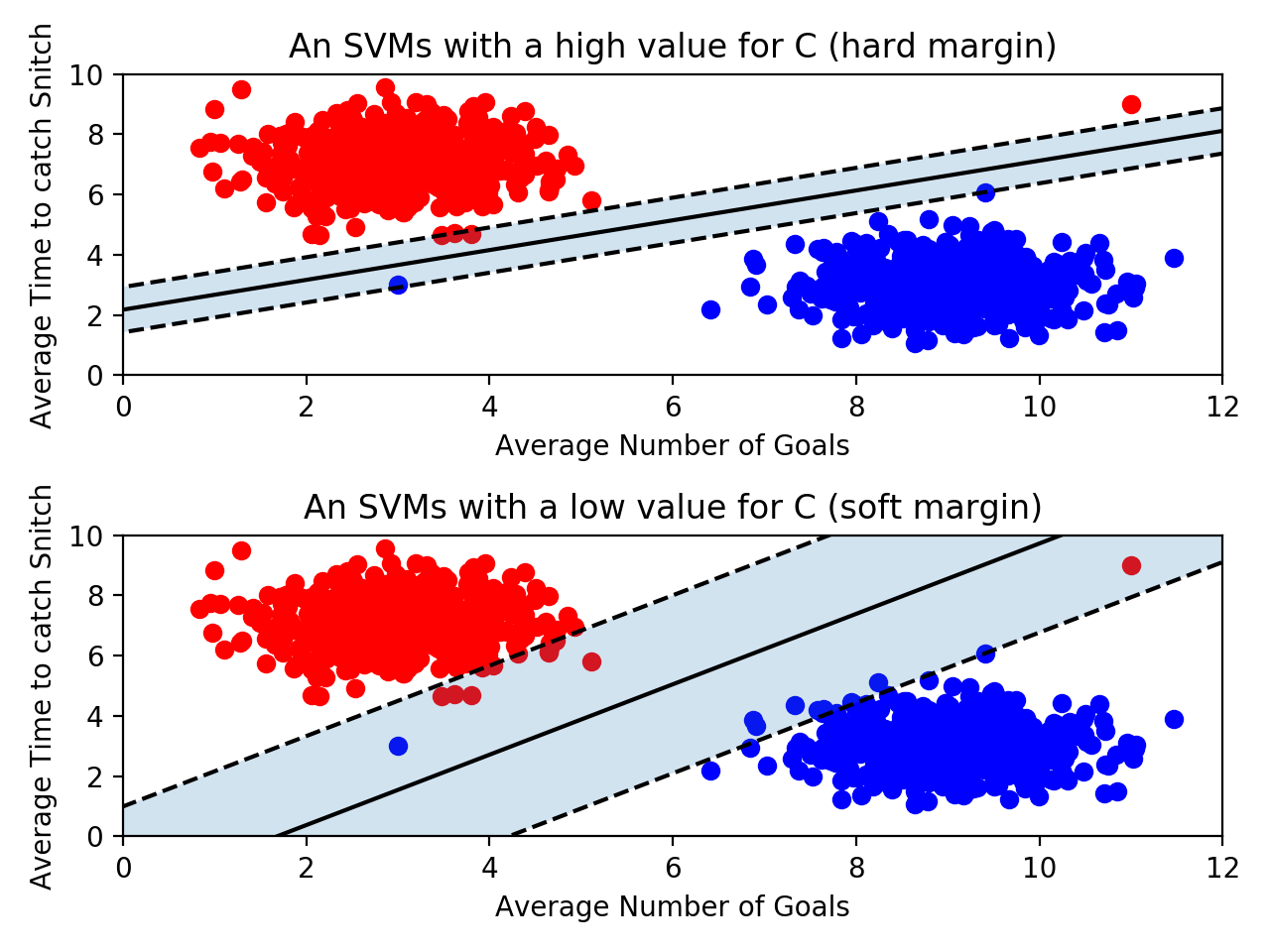
오른쪽 빨간색 이상치를 soft margin에서는 허용하는 것을 알 수 있다.
soft margin은 underfitting 문제가 있을 수 있다.
<2> Kernel Trick
SVM의 hyperparameter, 고차원 변환에 사용한다. (C -> Kernel Trick)
- Linear kernel
- Polynomial kernel: x^2
- Gaussian Kernel(RBF):〖exp{(-Y|(|x1-center1|)|^2 )}〗^2
- Sigmoid kernel 장점
분리가 확실한 데이터를 사용하면 정확도 높은 예측을 수행할 수 있다.
고차원에 효과적이다.
경계에 있는 서포트벡터만 사용하기 때문에 메모리 효율이 좋다.
단점
학습시간이 길어서 큰 데이터셋에 수행할 수 없다.
노이즈가 많은 데이터셋에는 잘 수행되지 않는다.
예측 결과에 대한 확률을 직접 제공하지 않는다. (교차 검증 시행착오를 통해 알아낼 수 있음)
SVM 수행 시 선택사항
- kernel function 어떤거 쓸건지 (linear, polynomial, RBF, sigmoid)
- kernel parameter 몇으로 할건지 (gamma, sigma)
- 최적 기준점 (hard vs soft, C)
끝.