최적화
이번 강에서는 딥러닝에서 사용되는 다양한 최적화 기법에 대하여 학습을 진행했다.
00. 학습 내용
- 최적화를 위한 개념에 대하여 학습
- 다양한 Gradient Descent Method에 대하여 학습
- 다양한 Regularization Method에 대하여 학습
01. 최적화를 위한 개념
- 모델을 최적화 한다는 것은 무엇일까? 개인적으로 모델을 최적화 한다는 것은 모델의 일반화 성능을 높이는 것이라고 생각한다.
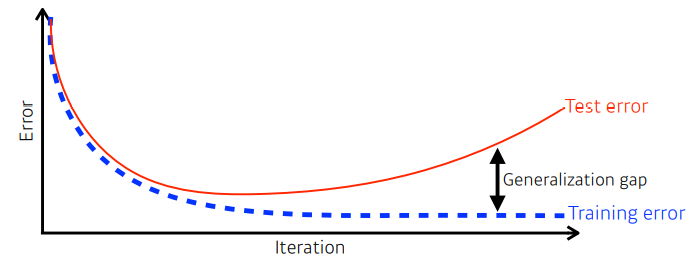
- 일반화(Generalization)란 위 그림처럼 학습 오차와 테스트(우리가 정답을 모르는 데이터) 오차 사이의 갭을 줄이는 것이다.
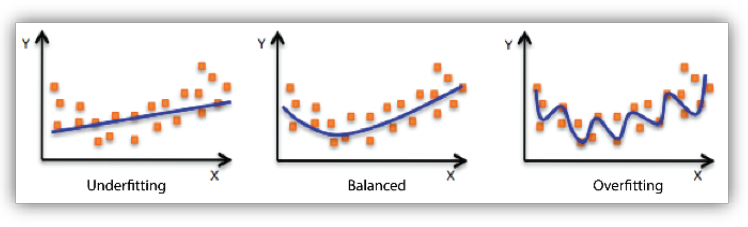
- 일반화 성능이 높은 모델이란 위 그림처럼 모델이 Overfitting 되지도, underfitting 되지도 않고 적절한 Balanced을 갖춘 모델을 말한다.
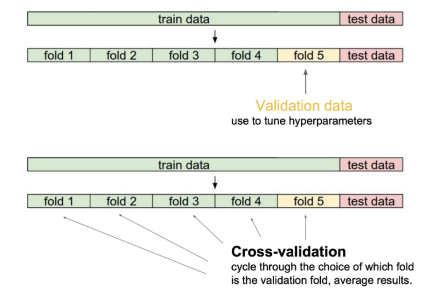
- 모델의 과적합과 과소적합을 검증하는 방법으로는 위처럼 Cross-Validation 방법이 있고, 이를 활용한 모델 성능 향상 방법 중 하나로 k-fold Ensemble 도 있다.
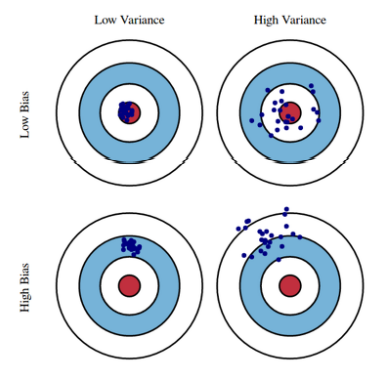
- 모델이 과적합과 과소적합이 발생하는 이유는 위처럼 모델이 높은 Bias을 가지거나, 높은 Variance을 가질 수도 있기 때문이다.
- 우리는 목적 함수를 bias + variance + noise 로 분해할 수 있을 텐데, 여기서 만약에 bias에 모델이 집중하게 되면 variance가 불안정해질 수도 있다. 이처럼 bias와 variance 서로 Trade-off 관계이다.
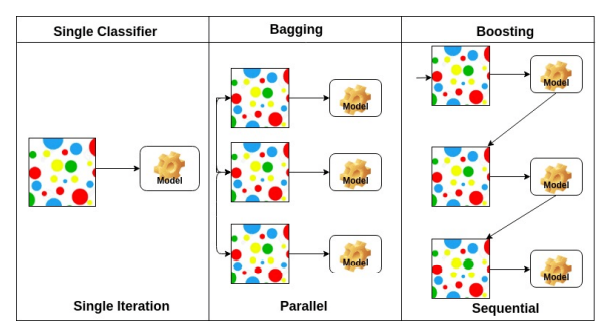
- 모델의 분산과 편향을 낮추는 하나의 방법으로 Bagging과 Boosting이 있다.
- Bagging은 하나의 데이터 셋에서 샘플링을 통해 여러개의 데이터셋을 만들어 병렬적으로 모델을 훈련시켜서 각 결과 값을 종합하는 방법론이다.
- Boosting은 하나의 모델을 순차적으로 학습시키면서 제대로 분류하지 못한 데이터에 가중치를 두어 그 데이터를 더 잘 분류하는 모델들을 순차적으로 학습시키며 최종적으로 여러 모델을 가중치에 따라서 종합하는 방법론이다.
02. Gradient Descent Method
- Gradient Descent Method는 학습 데이터를 어떻게 활용하는지에 따라서 크게 3가지로 나뉘어진다.
- Stochastic Gradient Descent
- 학습 한법에 1개의 Data를 활용하는 방식
- Mini-batch Gradient Descent
- 학습 한번에 임의의 개수에 Data를 활용하는 방식
- 우리가 NN을 학습시킬 때 대부분 활용하는 방식임 (Batch-size를 조정함)
- Batch Gradient Descent
- 학습 한법에 전체 Data를 활용하는 방식
- Stochastic Gradient Descent
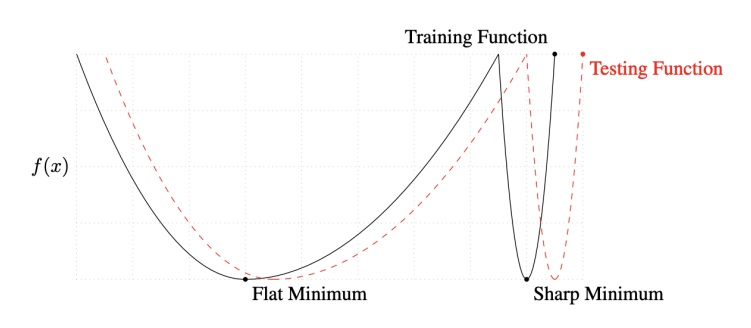
- 우리는 대부분 Mini-batch Gradient Descent를 활용하여 모델을 학습시키고, 이 방법에서 Batch-size는 매우 중요한 요소 중 하나이다.
- On Large-batch Training for Deep Learning: Generalization Gap and Sharp Minima (2017) 논문에서는 large Batch-size는 sharp minimum에 수렴한다고 했고, small Batch-size는 flat minimum에 수렴한다고 했다.
- 이 말을 직관적으로 해석하자면, small Batch-size를 통해서 많은 데이터 셋으로 다양한 함수를 근사화 함으로써, 조금더 적절한 함수(flat minimum)를 만들고 일반화 성능이 높아지는 것이라고 생각된다.
- Gradient Descent Method에는 다양한 Optimization Algorithm이 존재한다.
- Stochastic Gradient Descent
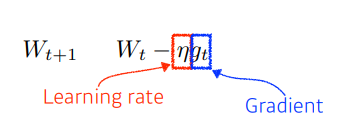
- 우리가 잘 알듯이 경사하강법을 통해 구한 기울기를 바탕으로 파라미터를 업데이트 하는 방식이다.
- Momentum
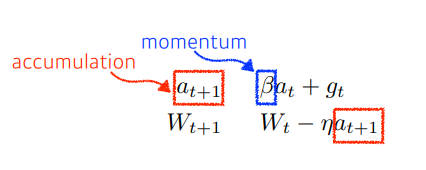
- 과거의 기울기 정보를 활용하여 파라미터를 업데이트 하는 방식으로, 식에서도 알 수 있듯이 모멘텀를 이용하여 기울기를 업데이트 하기 때문에 일정한 방향(과거에 이동한 방향)으로 이동하는 경향을 가지게 된다.
- Nesterov Accelerated Gradient
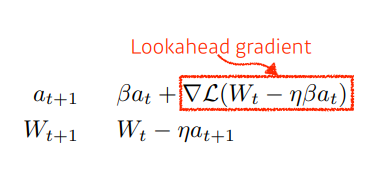
- Momentum과 조금 유사하지만, 식에서도 알 수 있듯이 기울기의 기울기를 사용하는 방식이기 때문에 Momentum 보다 조금더 빠르게 local minimum에 수렴하게 된다.
- Adagrad
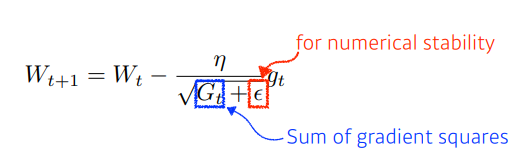
- 과거의 기울기의 정보를 모두 취합하여 기울기를 업데이트 방식으로, 식을 통해서도 알 수 있듯이 Epoch이 커지게 되면 기울기에 대한 값들이 많아져 분모가 커져서 업데이트가 잘 안될 수 있다.
- Adadelta
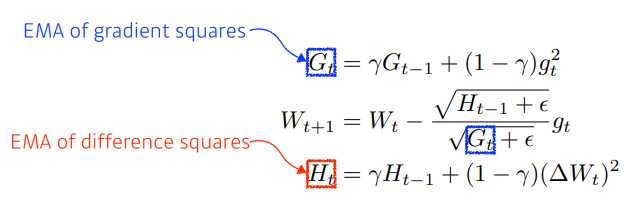
- Adagrad에 Epoch이 커지게 되면 업데이트가 잘 안되는 문제점을 EMA 방법을 이용해 해결한 방식이다. 그런데 본 문제의 단점은 learning rate가 존재하지 않
 는 다는 것이다.
는 다는 것이다.
- RMSprop
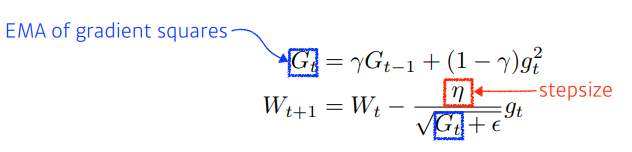
- Adadelta를 조금 변형해, learning rate를 추가한 방식이다.
- Adam

- RMSprop과 Momentum 방식을 서로 결합한 가중치 업데이트 방식으로, 오늘날에 가장 많이 사용되고 있는 Optimization Algorithm 이다.
- Stochastic Gradient Descent
03. Regularization Method
- 모델의 일반화 성능을 높일 수 있는 다양한 Regularization Method는 다음과 같다. (이 밖에도 다양한 방법이 존재함)
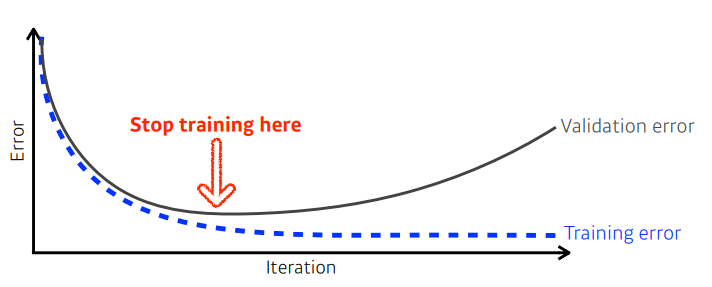
- Early Stopping, Validation error와 Training error의 gap이 커지는 부분에서 학습을 멈춤으로써 모델의 일반화 성능을 높일 수 있다
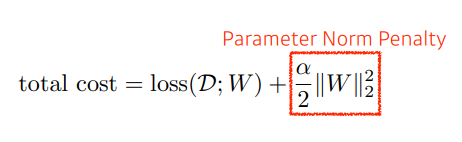
- Parameter Norm Penalty, Parameter에 규제를 가함으로써 함수를 smoothness하게 만들고, 적절한 크기의 Parameter 얻을 수 있다.
- 한쪽으로 너무 치우친 크기의 하나의 Parameter는 모델의 표현력에 제한을 준다. 따라서 Parameter의 크기를 모두 작지도 크지도 않으면서 적절한 크기의 Parameter로 만듬으로써 모델의 표현력을 높여야 한다. (여기서 말하는 크기는 1 , 2와 같은 수를 말함)
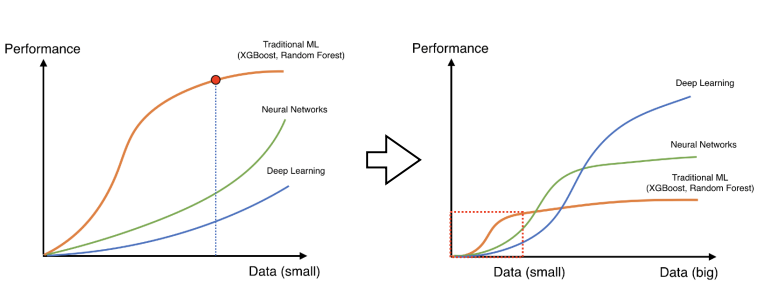
- Data Augmentation, 라벨에 영향을 주지 않는 선의 데이터 증강은 모델의 일반화 성능을 높일 수 있다.
- 다양한 방식의 데이터를 모델이 경험할 수 있기 때문에 모델의 표현력을 높여주는 것이라고 생각함

- Noise Robustness, inputs or weights에 랜덤한 noise를 추가함으로써 모델이 조금더 Robust하게 만들 수 있다.

- Label Smoothing, 두 정답셋을 다양하게 섞음으로써 모델을 조금더 Smooth 하게 만들 수 있고, 이는 모델에게 융튱성을 준다고 생각하며, 이를 통해서 모델의 성능을 높일 수 있다.
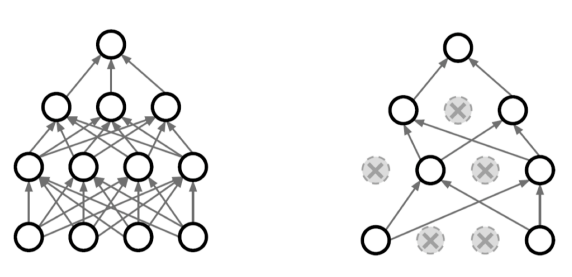
- Dropout, 랜덤하게 Weight를 죽여가며 학습함으로써, Weight의 표현력을 극대화해 모델을 성능을 높일 수 있다.
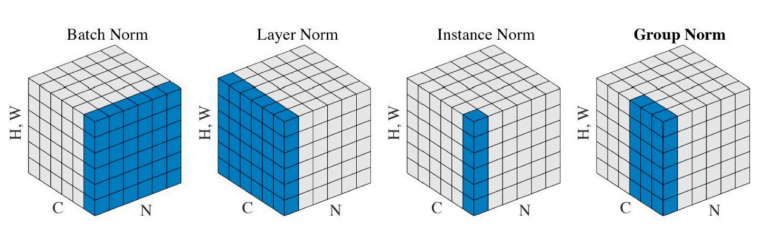
- Batch Normalization, 배치 단위의 데이터 셋을 정규화함으로써 모델의 성능을 높일 수 있다.(다양한 Normalization 방법이 존재함)
