들어가기에 앞서
5주차는 확실히 잘 풀지 못했다. 일단 문제가 최근 들어 풀었던 것 중 가장 어렵다고 느끼기도 했고, 주차 초반에 심한 독감으로 인해 아무것도 못했다고 할 수 있다..
켈록켈록, 에츄에츄, 푸엣췽~! ㅋㅋㅋㅋㅋㅋㅋ

그래서 같이 스터디하시는 분 한테 골드급 문제는 힌트만 받았다. 예를 들어, 이 문제는 이 알고리즘이에요~ 하는 식으로 말이다.
그런데 말입니다~ 각자 푸는 방식이 달라서 그런지 힌트가 크게 도움은 안됐다.. 11066 문제정도? 흐음 이 문제는 아마 다음 주차 문제에서 비슷한 문제를 풀게되는데, 이번 주차에서는 점화식을 세우기 보다는 원리만 설명하도록 하겠다.
내가 생각했을 때, 점화식을 먼저 보는건 정말 정말 기억에 안남는다. 원리를 알면 점화식은 알아서 도출되는 것이고 그걸 스스로 해야 기억에 오래 남는다고 생각한다!!
오늘도 실버급 문제부터 시작!
15666
N과 M 수열 문제에서 12번이다.

해당 시리즈의 문제는 질리도록 조건이 비슷하기 때문에 간단하게 설명하도록 하겠다.
- 수를 선택할 때, 현재 선택하려고 하는 수가 이전에 선택한 수보다 커야한다. 그래야지만 비 내림차순으로 수열을 만들 수 있다.
- c++에서는 정말 편리하게도 set을 이용해 set 내부에 vector를 담을 수 있다. 심지어 vector 자체의 원소들을 기준으로 중복 여부도 관리해준다. 따라서 만들어진 수열이 set에 담겨있다면 담지 않고, 없으면 담는 식으로 수열을 하나씩 만들어 나간다.
- 사전 순으로 출력해야하는데 c++의 set은 정렬도 해준다... 그냥 순서대로 출력하쟈!
#include <iostream>
#include <vector>
#include <algorithm>
#include <set>
using namespace std;
int N, M;
vector<int> numbers;
vector<int> per;
set<vector<int>> s;
void permutation(int num, int depth) {
if (depth == M) {
s.insert(per);
}
else {
for (int i = 0; i < numbers.size(); i++) {
int cn = numbers[i];
if (cn >= num) {
per.push_back(cn);
permutation(numbers[i], depth + 1);
per.pop_back();
}
}
}
}
int main() {
cin >> N >> M;
int input;
for (int i = 0; i < N; i++) {
cin >> input;
numbers.push_back(input);
}
permutation(0, 0);
for_each(s.begin(), s.end(), [](vector<int> v) {
for (int i = 0; i < v.size(); i++) {
cout << v[i] << " ";
}
cout << '\n';
});
}9020
골드바흐의 추측이다. 에라토스테네스의 체를 이용하면 쉽게 풀 수 있으나, 그렇게 하지 않아도 풀 수 있다.

1. 1부터 10000까지 소수를 먼저 다 찾는다. 두 수를 더할 때마다 각 수가 소수인지 체킹하는 것보다 빠를 것이라고 생각했다.
2. 입력된 수의 절반을 기준으로 2까지 내려가면서 더해지는 두 수가 소수인지 확인한다.
3. 절반을 기준으로 내려가는 이유는 찾은 두 소수의 차이가 가장 작아야하는데, 해당 방식으로 할 경우 가장 작은 경우부터 찾는 것이 가능하다.
#include <iostream>
#include <vector>
#include <set>
using namespace std;
int T;
int gap;
pair<int, int> answer;
set<int> special_numbers;
vector<int> comb;
bool check_num(int num) {
for (int i = 2; i <= (int)num / 2; i++) {
if (num % i == 0)
return false;
}
return true;
}
void find_pair(int input) {
int half = (int)input / 2;
for (int i = half; i > 1; i--) {
int temp = input - i;
if (special_numbers.find(i) != special_numbers.end() && special_numbers.find(temp) != special_numbers.end()) {
cout << i << " " << temp << '\n';
break;
}
}
}
int main() {
special_numbers.insert(2);
special_numbers.insert(3);
for (int i = 4; i < 10001; i++) {
if (check_num(i))
special_numbers.insert(i);
}
cin >> T;
int input;
for (int i = 0; i < T; i++) {
cin >> input;
find_pair(input);
}
}11066

먼저 내가 최초에 만든 dp 배열은 다음의 형태를 가지고 있다. 해당 경우는 1이 다섯 개가 입력으로 들어간 경우이다.
그림의 오른쪽 아래에 있듯이 파란색 빗금 사각형을 만드는 경우는 세 가지가 존재한다.
1. dp[0][3] = dp[0][0] + dp[1][3]
2. dp[0][3] = dp[0][1] + dp[2][3]
3. dp[0][3] = dp[0][2] + dp[3][3]각각,
1. 1 크기의 파일과 3 크기의 파일을 합치는 경우 (<1>, <1, 1, 1>)
2. 2 크기의 파일과 2 크기의 파일을 합치는 경우 (<1, 1>, <1, 1>)
3. 3 크기의 파일과 1 크기의 파일을 합치는 경우 (<1, 1, 1>, <1>)이게 엄청 큰 힌트이다.
그런데 위 그림과 같이 풀고 입력으로 들어온 1 다섯 개를 전부 합치는데 필요한 최소 비용은 dp[0][4]에 오는 값으로 14가 온다. 그러나 이것은 틀렸다. 실제로는 12가 와야한다.
그림에서는 계산을 잘못하고 있는데,
예를 들어서 파란색 빗금 사각형을 만들기 위해 초록색과 초록색을 더하는 경우를 보자.
<1, 1, 1> 3개를 합치는 비용 5 + 파일 3개의 크기 5 + 파일 1개의 크기 1
여기서 큰 오류는 파일 3개의 크기는 5가 아니다. 그러니까 dp에 저장된 내용은 파일을 합치는데 쓰이는 비용이지 실제 파일 크기가 아니기 때문에 오류가 발생한다.
이 경우, 입력 예제 2에서 1592라는 값이 나오는데 만약 나와 비슷한 상황이라면 위의 오류를 수정하길 바란다
실수한 내용을 정리하면 다음과 같다.
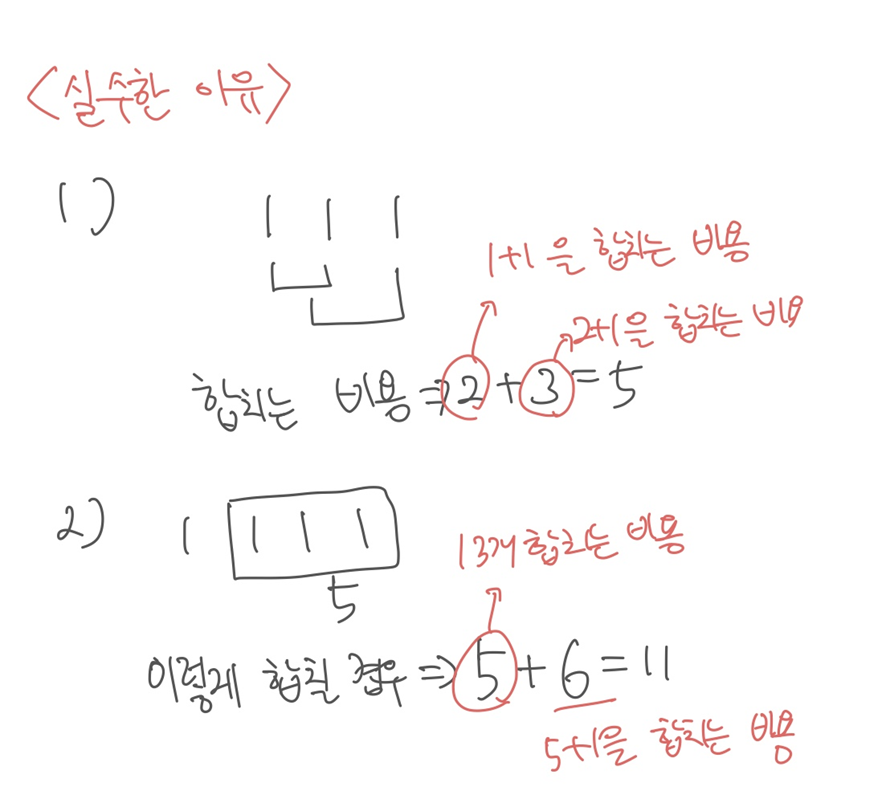
1번의 경우 우연히 계산될 수 있는 경우지만, 2번의 경우에는 다음과 같이 계산되어야한다.
실제로는,파일 3개를 합치는 비용 5 + 파일 1개를 합치는 비용 0 + 두 파일의 크기 합 (1 + 3) 을 해서 9가 나와야한다!
그래서 최종적으로 dp 배열에는 해당 파일을 만드는데 필요한 비용만을 저장하고 (원래는 대각선에 해당 파일의 크기를 담고 있었다!) sum 배열에 파일합을 저장함으로써 파일의 크기를 유추하게 된다.
sum[i] = 1부터 i까지 파일의 합이다. 예를 들어, 4~5까지의 파일 합은 sum[5] - sum[3]을 통해서 구할 수 있다.
그래서 위 그림에서 2번은
dp[0][3] = dp[0][0] + dp[1][3] + (sum[3] - 0) 마지막이 0인 이유는 sum[-1]은 아무것도 없는 것을 뜻하므로 0이된다.
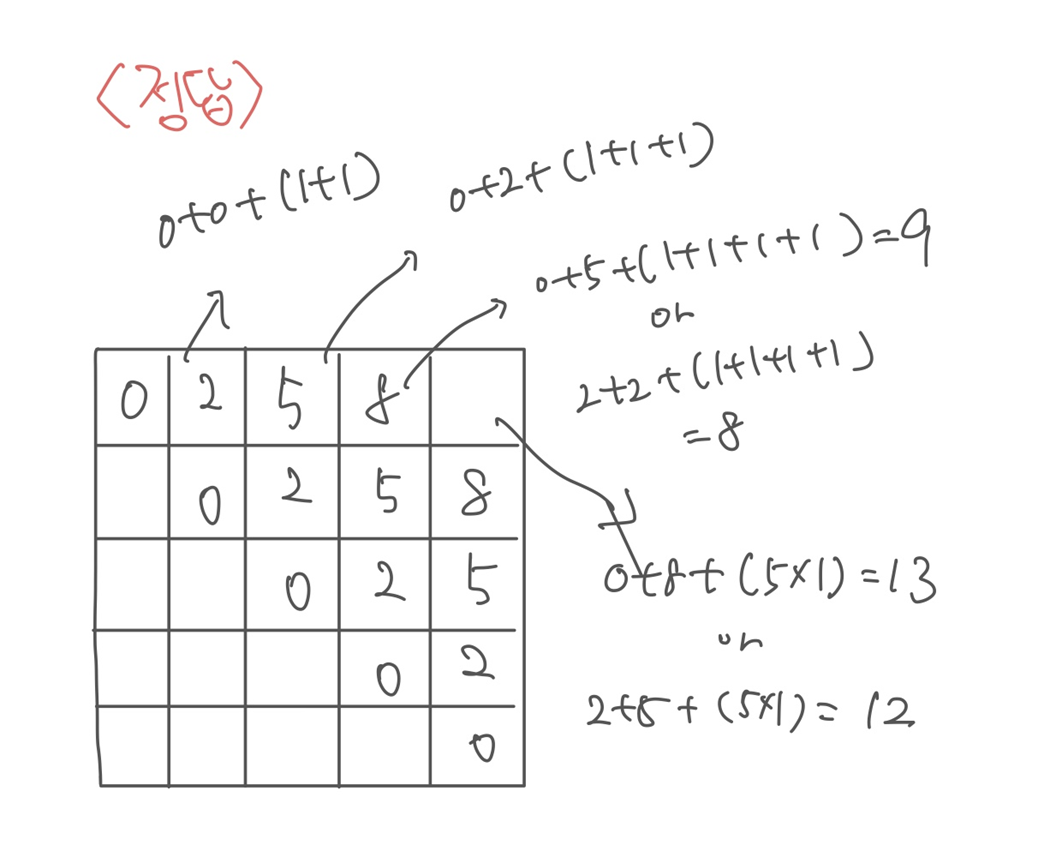
최종적으로 생성한 dp는 다음과 같다. 정상적으로 잘 계산되어서 최종 칸에는 12가 오게된다. 실제로 정답도 12이다!
만약 이 문제에서 헤매고 있다면, 입력으로 1, 1, 1, 1 또는 1, 1, 1, 1, 1과 같이 1로만 구성된 입력을 넣는다고 가정하고 직접 dp를 만들면서 풀어보면 코드로도 위의 dp 배열을 다 채울 수 있을 것이다.
코드는 아래와 같다.
#include <iostream>
#include <algorithm>
#include <memory.h>
#include <climits>
using namespace std;
int K;
int dp[500][500];
int nums[500];
int sums[500];
int main() {
int T;
cin >> T;
for (int i = 0; i < T; i++) {
cin >> K;
memset(sums, 0, sizeof(sums));
fill(&dp[0][0], &dp[500-1][500], INT_MAX);
int sum = 0;
for (int j = 0; j < K; j++) {
cin >> nums[j];
sum += nums[j];
sums[j] = sum;
dp[j][j] = 0;
}
for (int j = K - 1; j >= 0; j--) {
for (int k = j; k < K; k++) {
for (int l = k + 1; l < K; l++) {
if (j != 0) {
dp[j][l] = min(dp[j][l], dp[j][k] + dp[k + 1][l] + (sums[l] - sums[j - 1]));
}
else {
dp[j][l] = min(dp[j][l], dp[j][k] + dp[k + 1][l] + sums[l]);
}
}
}
}
cout << dp[0][K - 1] << '\n';
}
}1005
스터디를 같이 하시는 분의 경우 우선 순위 큐를 통해 풀었다고 했다. 그런데 문제를 조금 읽어보니 간단한 BFS를 통해서 풀 수 있을 것 같았다.
추후에 알았지만 해당 방식은 위상 정렬을 뜻한다고 한다. 이전 조건을 만족해야 다음으로 넘어갈 수 있기 때문에?? 그러나 아직 위상정렬을 잘 모르기 때문에 여기서 다루지는 않겠다.
이 문제의 경우 어려웠던 점과 해결 방식에 대해서 서술하는 식으로 풀이를 해보겠다.
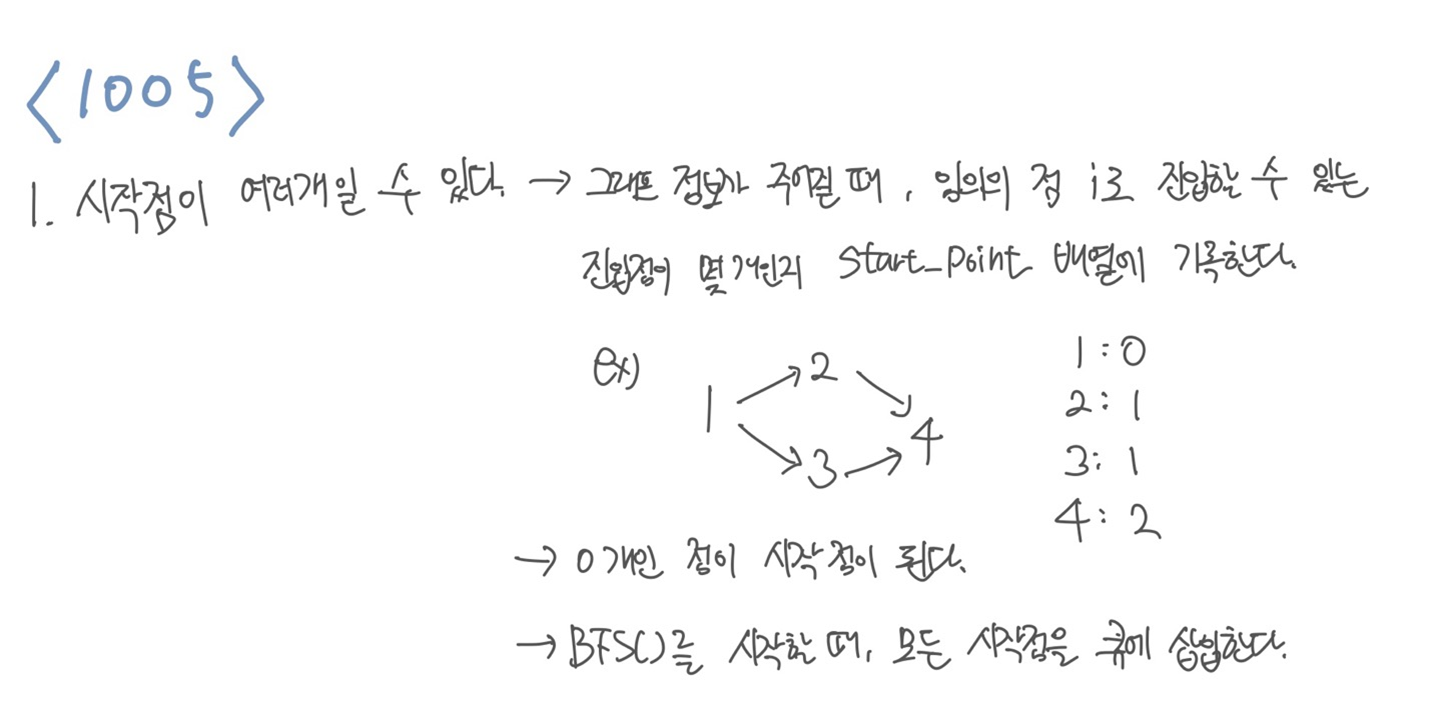
처음에, 나는 시작점이 한 개만 있다고 생각했다. 그러나 그건 큰 오산이었다. 그러나 여러 개의 시작 점이 존재할 수 있기 때문에 그래프 정보가 주어질 때, 시작점이 무엇인지 알고 있어야 했다. 따라서 start_point라는 배열에 x -> y로 가는 경우 start_point[y]++ 해줌으로써 y의 선행점이 한 개 존재합니다~ 라고 표시를 하는 식으로 했다.
이렇게 되면 최종적으로 선행점이 하나도 없는 점은 시작점이기 때문에 BFS를 시작할 때 제일 먼저 queue에 삽입된다.

BFS의 queue에 다음 정점 i를 삽입하기 위해서는 i로 가는 모든 진입점을 탐색한 후에 가능하다. 왜냐하면 i 이전의 모든 건물들이 다 세워진 이후에야 i의 건물을 세울 수 있기 때문이다.
예시는 위의 그림을 살펴보면 바로 이해할 수 있다.

나의 경우 처음에 BFS라고 생각하여 방문 배열을 두었다.
그래서 visit 배열의 i에는 i정점의 건물이 세워지기까지의 시간을 기록하는 식으로 하였는데, 실제로는 방문 배열은 아니다. DP랑 비슷한 것 같다.
특이한 경우는 원래는 덜 걸리는 시간을 담아야하지만 더 오래걸리는 쪽을 담아야한다. 아까와 마찬가지로 본 정점으로 진입할 수 있는 이전의 모든 정점들의 건물들이 다 세워져야지 본 정점의 건물이 세워질 수 있기 때문이다.
이 3 가지의 조건만 만족하여 소스 코드를 짠다면, 바로 정답을 도출할 수 있다.
#include <iostream>
#include <vector>
#include <queue>
#include <memory.h>
using namespace std;
int N, K, W;
int dp[500][500];
int times[1000];
vector<int> graph[1000];
int visit[1000];
int start_point[1000];
// Node Number, time
queue<int> q;
void bfs() {
memset(visit, -1, sizeof(visit));
for (int i = 0; i < N; i++) {
if (start_point[i] == 0) {
q.push(i);
visit[i] = times[i];
}
}
while (!q.empty()) {
int cn = q.front();
int c_time = visit[cn];
q.pop();
for (int i = 0; i < graph[cn].size(); i++) {
int nn = graph[cn][i];
visit[nn] = max(visit[nn], c_time + times[nn]);
if (start_point[nn] > 1) {
start_point[nn] -= 1;
}
else if (start_point[nn] == 1) {
q.push(nn);
start_point[nn] -= 1;
}
}
}
}
int main() {
int T;
cin >> T;
for (int i = 0; i < T; i++) {
cin >> N >> K;
for (int n = 0; n < N; n++) {
cin >> times[n];
}
int start, end;
memset(start_point, 0, sizeof(start_point));
for (int k = 0; k < K; k++) {
cin >> start >> end;
graph[start - 1].push_back(end - 1);
start_point[end - 1] += 1;
}
int answer;
cin >> answer;
bfs();
cout << visit[answer - 1] << '\n';
for (int j = 0; j < 1000; j++)
graph[j].clear();
}
}소감
몸이 아파서 힘든 주차였다. 근데 벌써 5주차라니!!!
다음은 설 연휴가 끼여있지만 열심히 해보도록 하쟈. 이렇게 내가 푼 알고리즘 문제들을 계속 기록해나갈 수 있는 내가 되었으면 좋겠다.
오늘 토익 시험도 쳤는데 점수 잘나오게 해주세요~ 아 그리고 solved.ac에서 확인한 바로는 원래 티어가 골드 5였는데 골드 4로 승급되었다. 짝짝짝~~
지금 스터디 하는 친구들이 다 골드 2에 있는데 얼른 따라갈 수 있었으면 좋겠다.
