들어가기에 앞서
1주차 때는 c++ 풀이라는 제목으로 글을 작성하고 아이디어만 공유한다고, 코드를 하나도 올리지 않았다.
그 당시에는 문제 풀이를 참고하는 사람 입장에서 코드가 보이는 것보다 간단한 아이디어가 공유되는 것이 좋다고 생각했다. 나의 경우 백준 문제를 풀다 막힐 때, 풀이를 들어갔는데, 다짜고짜 이건 이래서 이 코드구, 저건 저래서 저 코드고 식으로 설명이 되어있으면 바로 창을 닫아버린다.
나는 단지 아이디어가 궁금할 때가 많다. 구현은 내가 하고 싶어!!! 이런 금쪽이 마인드일지도 모른다 ㅋㅋㅋㅋ

그러나 아이디어만 가지고 한계에 맞닥뜨렸을 때, 이 아이디어가 어떻게 코드로 구현되는지를 참고할 수도 있어야겠다는 생각이 들었다.
그리고 내 게시글의 특징인데 매번 말투가 조금씩 바뀌는 것 같다! 아무래도 그 때 그 때 글을 쓰는 분위기가 조금 차이가 나서인 듯 하다.
백준 11725
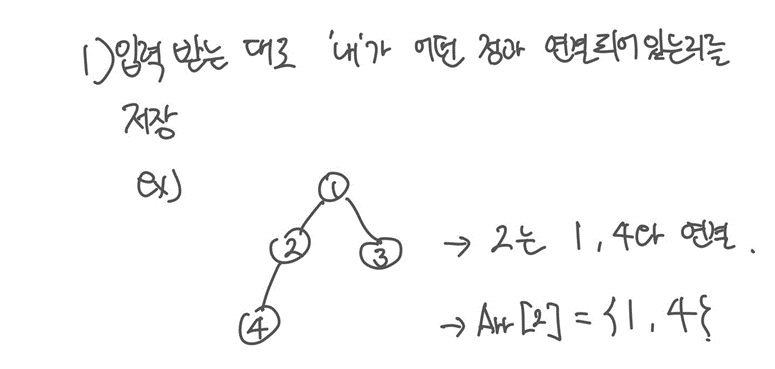
이 문제는 트리의 부모를 찾는 문제다.
정점은 그림과 같이 순서대로 주어지지 않고, 무작위로 주어질 때, 특정 정점 i의 부모 노드가 무슨 노드인지를 알고 있어야 한다.
입력받으면서 특정 정점 i가 다른 어떤 점과 연결되어있는지를 기록한다.
위의 그림에서 예를 들면, 2는 1, 4와 연결이 되어있다. 따라서 Arr[2] = {1, 4} 식으로 기록하면 된다.
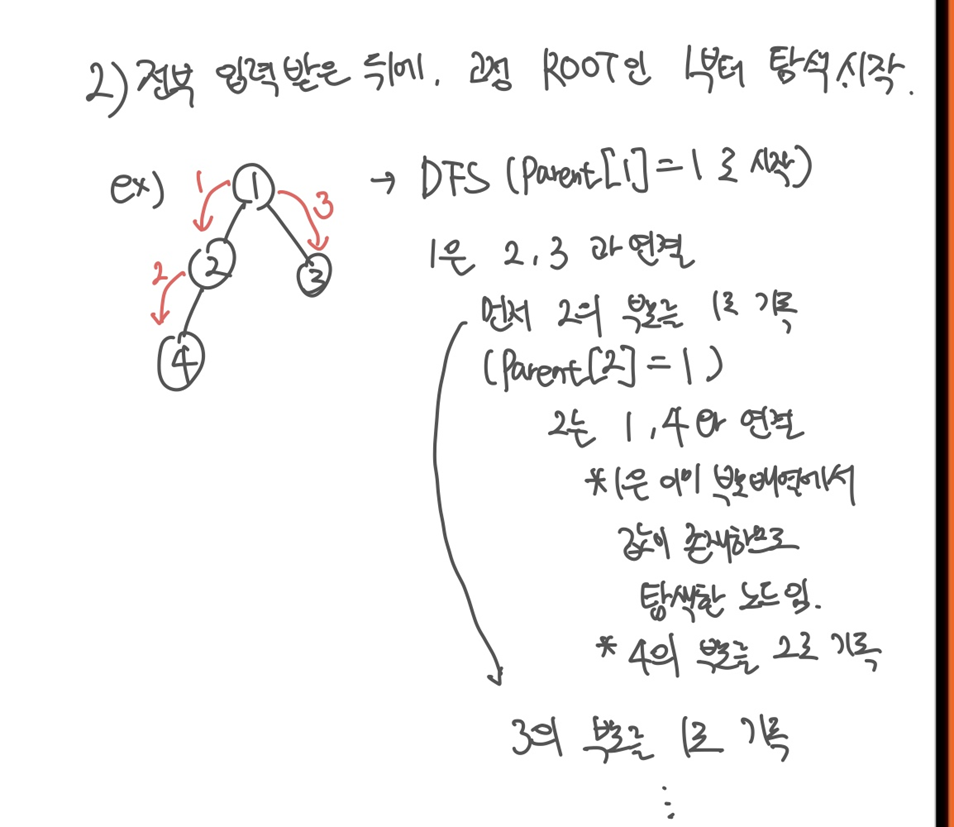
입력이 완료되면 문제에서 루트 노드가 1로 고정이기 때문에 1부터 DFS로 탐색을 시작한다. 사실 트리를 탐색하는 것이기 때문에 BFS여도 크게 문제는 없다.
시작하기 전에 루트 노드인 1의 부모는 자기 자신인 1로 표시한다. 따라서 '내'가 누구를 부모로 가지고 있는지 저장하는 배열인 Parent을 두고 트리를 순회하기 전에 Parent[1] = 1로 시작하면 된다. 이는 단순하게 1의 부모가 1인 것을 의미하기도 하지만 다른 의미에서는 1번 노드를 이미 탐색한 적이 있다고 해석할 수 있다. 즉, 방문 확인용 배열로도 사용될 수 있다.
1은 2, 3과 연결되므로 DFS에 따라 2번 노드로 이동한다. 그리고 2의 부모를 1로 기록한다. 즉 Parent[2] = 1이 된다. 2는 1과 4와 연결이 되어있는데 Parent배열에서 1은 이미 값을 지니고 있으므로 탐색한 적이 있다는 것을 의미하기 때문에 4번 노드로 이동한다.
4번 노드의 부모를 2로 기록한다. Parent[4] = 2. 4번 노드는 다른 노드와 연결되어있지 않으므로 더 이상 탐색하지 않고, 다시 돌아오게 된다.
이와 같은 과정을 반복하면 모든 정점의 부모를 기록할 수 있다.
또 정답 출력과정에서 정점 2부터 순서대로 N까지 부모를 출력하기 때문에 Parent 배열을 2부터 N까지 순서대로 출력하기만 하면 맞을 수 있다.
정말 중요한 사실
출력에서 나는
cout << {출력물} << endl;을 써서 출력을 했는데, 시간초과가 발생했다. 나는 내 알고리즘에 문제가 있는 줄 알았는데 endl이 단순 개행 말고도 버퍼를 비우는 기능을 수행하기 때문에 시간을 많이 잡아먹는다고 한다. 따라서 cout << {출력물} << '\n'; 과 같이 사용하는 것이 중요하다.
코드는 아래와 같다.
#include <iostream>
#include <vector>
using namespace std;
int parent[100001];
vector<int> v[100001];
void dfs(int nodeNum) {
for (int i = 0; i < v[nodeNum].size(); i++) {
int child = v[nodeNum][i];
if (parent[child] == 0) {
parent[child] = nodeNum;
dfs(child);
}
}
}
int main() {
int N;
int n1, n2;
cin >> N;
parent[1] = 1;
for (int i = 0; i < N - 1; i++) {
cin >> n1 >> n2;
v[n1].push_back(n2);
v[n2].push_back(n1);
}
dfs(1);
// endl은 개행 뿐 아니라 버퍼를 비워주는 일도 수행하기 때문에
// '\n' 보다 많이 느리다.
for (int i = 2; i <= N; i++) {
cout << parent[i] << '\n';
}
}백준 16173

이 문제의 조건을 정리하면 위의 그림과 같다.

(0, 0)을 시작으로 BFS 또는 DFS 탐색을 하여 최종 목적지인 -1에 도달 가능한 경우가 하나라도 존재하면 전역 변수 Check와 같은 것을 True로 변경하는 식으로 하여 문제를 풀 수 있다.
최종 출력 전에 Check 값에 따라 결과를 다르게 출력하면 쉽게 문제를 풀 수 있다.
코드는 다음과 같다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int N;
int map[3][3];
int visit[3][3] = { 0, };
bool check = false;
void dfs(int x1, int x2) {
if (map[x1][x2] == -1) {
check = true;
}
else if (!visit[x1][x2]) {
visit[x1][x2] = 1;
if (x1 + map[x1][x2] <= N)
dfs(x1 + map[x1][x2], x2);
if (x2 + map[x1][x2] <= N)
dfs(x1, x2 + map[x1][x2]);
}
}
int main() {
cin >> N;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
int temp;
cin >> temp;
map[i][j] = temp;
}
}
dfs(0, 0);
if (check) {
cout << "HaruHaru" << '\n';
}
else {
cout << "Hing" << '\n';
}
}백준 1987

위에서 풀었던 문제와 마찬가지로 조건은 다음과 같다.
(0, 0)을 시작으로 특정 지점까지 이동할 때, 내가 밟은 칸이 무엇인지 기억하기 위해서는 DFS를 사용하여야 한다.

어떤 알파벳을 밟았는지 확인하는 배열이 필요하고, 칸을 밟을 때마다 해당 칸의 알파벳을 밟았다고 체크한다.
더 이상 이동할 수 없으면, 해당 칸까지 몇 칸을 이동하였는지 기록한다. 이전에 기록된 칸 수보다 많으면 현재 기록이 최대가 된다.ㅣ
코드는 다음과 같다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int R, C;
char arr[20][20];
int alpha[26] = { 0, };
int maxNum = 0;
void dfs(int x1, int x2, int depth) {
int index = arr[x1][x2] - 65;
if(!alpha[index]) {
maxNum = max(maxNum, depth);
alpha[index] = 1;
// 상
if (x1 - 1 >= 0)
dfs(x1 - 1, x2, depth + 1);
// 하
if (x1 + 1 < R)
dfs(x1 + 1, x2, depth + 1);
// 좌
if (x2 - 1 >= 0)
dfs(x1, x2 - 1, depth + 1);
// 우
if (x2 + 1 < C)
dfs(x1, x2 + 1, depth + 1);
alpha[index] = 0;
}
}
int main() {
cin >> R >> C;
for (int i = 0; i < R; i++) {
for (int j = 0; j < C; j++) {
cin >> arr[i][j];
}
}
dfs(0, 0, 1);
cout << maxNum << '\n';
}백준 17141
정말 정말 어려운 문제였다. 최근 풀었던 문제 중에 제일 어려웠던 것 같다. 일단 아이디어를 먼저 공유한다.

먼저 조합을 구해야한다. 그리고 특정 조합에서 바이러스를 퍼뜨리고 BFS를 통해서 바이러스가 맵 전체에 퍼지는지 몇 초가 걸리는지 visit 배열에 하나 하나 기록한다. 바이러스가 전부 퍼지고 나서 visit 배열에서 가장 큰 수를 가져오면 해당 맵에 바이러스가 퍼질 때까지 걸린 시간을 알 수 있다.
이 과정을 모든 조합에 대해 반복하고, 가장 적게 걸린 시간을 추출하면 된다.
코드는 아래와 같다.
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
#include <memory.h>
#include <limits.h>
using namespace std;
int N, M;
int arr[50][50] = { 0, };
int visit[50][50];
int dx[] = { -1, 1, 0, 0 };
int dy[] = { 0, 0, -1, 1 };
int answer = INT_MAX;
vector<pair<int, int>> find_comb;
vector<pair<int, int>> virus_position;
queue<pair<pair<int, int>, int>> q;
bool check(int x, int y) {
if (x >= 0 && x < N && y >= 0 && y < N)
if (arr[x][y] != 1 && visit[x][y] == -1)
return true;
return false;
}
int check_board() {
int cnt = 0;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
// 실제 지도에서 벽이면 확인할 필요가 없음
if (arr[i][j] == 1)
continue;
// 벽이 아닌 곳 중에서 방문되지 않은 곳이 하나라도 있으면, 바이러스가 전체적으로 퍼질 수 없는 경우임
else if (visit[i][j] == -1)
return -1;
else
cnt = max(cnt, visit[i][j]);
}
}
return cnt;
}
void bfs() {
while (!q.empty()) {
int cx = q.front().first.first;
int cy = q.front().first.second;
int cs = q.front().second;
q.pop();
for (int j = 0; j < 4; j++) {
int nx = cx + dx[j];
int ny = cy + dy[j];
if (check(nx, ny)) {
q.push(make_pair(make_pair(nx, ny), cs + 1));
visit[nx][ny] = cs + 1;
}
}
}
int check = check_board();
if (check != -1)
answer = min(answer, check);
}
void combination(int now, int pos) {
if (now == M) {
memset(visit, -1, sizeof(visit));
for (int i = 0; i < find_comb.size(); i++) {
int x = find_comb[i].first;
int y = find_comb[i].second;
q.push(make_pair(find_comb[i], 0));
visit[x][y] = 0;
}
bfs();
}
for (int i = pos; i < virus_position.size(); i++) {
find_comb.push_back(virus_position[i]);
combination(now + 1, i + 1);
find_comb.pop_back();
}
}
int main() {
cin >> N >> M;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
cin >> arr[i][j];
if (arr[i][j] == 2)
virus_position.push_back(make_pair(i, j));
}
}
combination(0, 0);
if (answer == INT_MAX)
cout << -1 << '\n';
else
cout << answer << '\n';
return 0;
}사실 조합만 잘 구해지면 그 이후로는 큰 어려움이 없다.
그리고 visit 배열에서 임의의 칸 i에 적힌 숫자의 의미는 i칸까지 바이러스가 퍼진데 걸린 시간이라는 것을 명심하자. 그러면 굳이 bool 자료형을 가진 visit 배열과 따로 몇 초 걸리는지 세는 cnt 변수를 가질 필요가 없다.
결론
이번 주는 DFS, BFS 문제를 주로 다루었는데 확실히 아직 많이 부족한 것 같다.
특히 BFS와 DFS를 좀 바로 바로 코딩이 될 수 있게까지 몸에 익히려면 아직은 턱없이 부족하다는 생각이 든다. 앞으로도 조금 더 열심히 해야겠다 ㅠㅠ
