[프로그래머스-자바] 두 원 사이의 정수 쌍

📜 문제

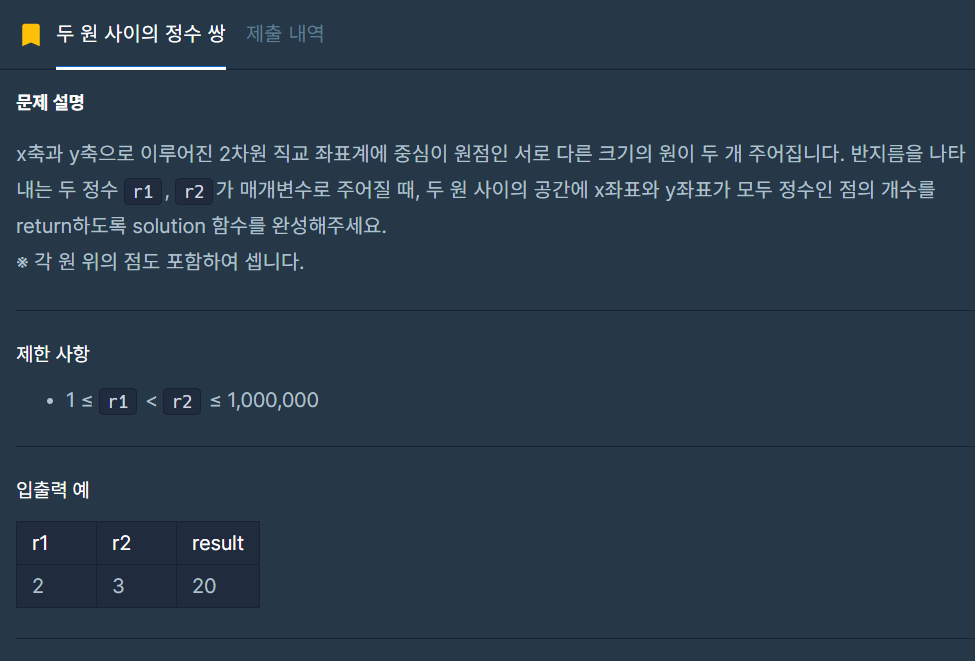
• 두 원의 반지름이 주어진다.( 1<=r1<r2<=1,000,000 )
• 두 원 사이에 위치한 좌표의 개수 구하기 (단, x,y 는 정수)

---

풀이 과정

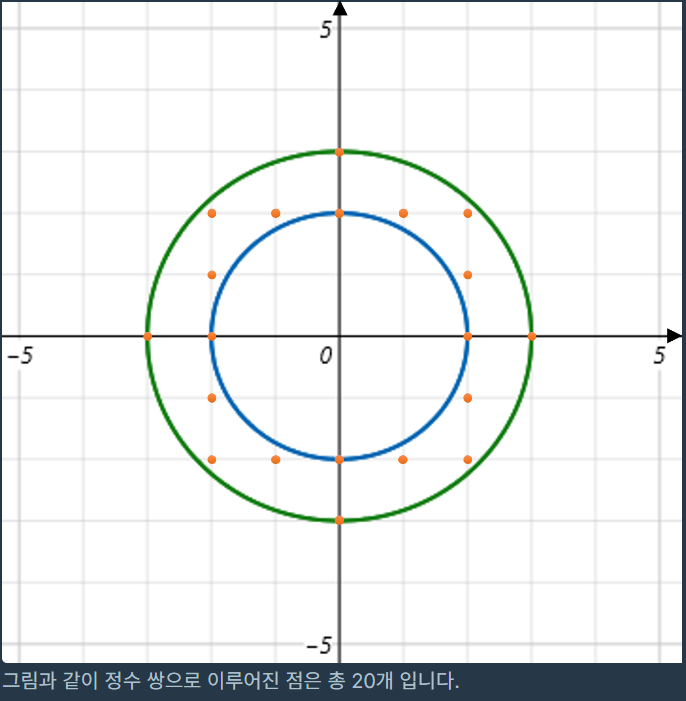
1. 두 원의 중심은 원점이므로 1, 2, 3, 4분면에 존재하는 좌표는 대칭이다.
   즉, 한 사분면에 있는 좌표의 개수만 구하면 답을 도출해 낼 수 있다. (4 곱하면 됨)

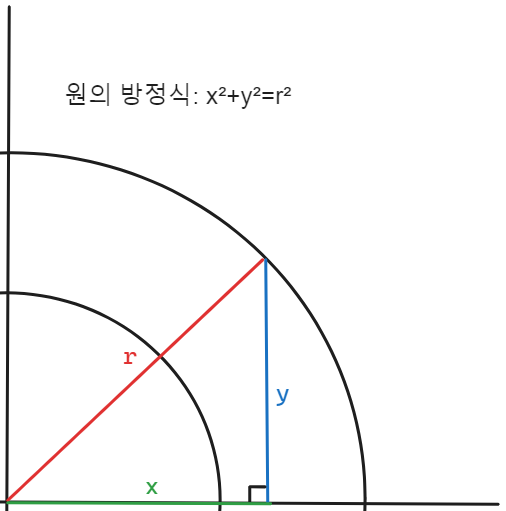
2. 원 사이에 있는 좌표를 구하기 위해선 원의 방정식을 이용하면 된다.
   원점 (n,m), 원의 방정식: (x-n)²+(y-m)²=r²
   

• 좌표는 r2를 반지름으로 갖는 원의 내부에 위치해 있어야 한다. (x²+y²<=r2²)
  - x² + y² <= r2² ＝ x <= sqrt(r2²-y²) 또는 y <= sqrt(r2²-x²)

ex) y = 1, r2 = 3
x2 <= sqrt(9-1) = √8 (2.xxxx)
x2 =2

3. 큰 원의 내부 좌표에서 작은 원 내부에 있는 좌표는 제외해야 한다.

즉, 작은 원의 외부에 존재해야 한기 때문에 우리는 위 수식을 그대로 이용하되, 소수점에서 올림한 값을 취하면 된다.

ex) y = 1, r1 = 2
x1 <= ceil (sqrt(4-1)) = ceil(√3) (1.xxxx) = 2
x1 =2

4. x2~x1 사이 좌표 개수 구하기
   x2 - x1 + 1 값이 y = 1일 때 두 원 사이의 정수 좌표 개수이다.
   즉, 2 - 2 + 1 = 1 개이다.

---

🍳 전체 소스 코드

class Solution {
    public long solution(int r1, int r2) {
       long answer = 0;
        for(int y=1; y<=r2;y++){
            int x2 = (int)Math.sqrt(Math.pow(r2,2) - Math.pow(y,2));
            int x1 = (int)Math.sqrt(Math.pow(r1,2) - Math.pow(y,2));
            answer +=x2-x1+1;
        }
        return answer*4;
    }
}

---

✨ 결과

못 풀어서 답 봤다.
흥 그래도 다음에 볼 때는 확실하게 풀 수 있을 거다.

출처를 남기고.. 이만. ..
given-dev, [Programmers-Java] 두 원 사이의 정수 쌍