📜 문제

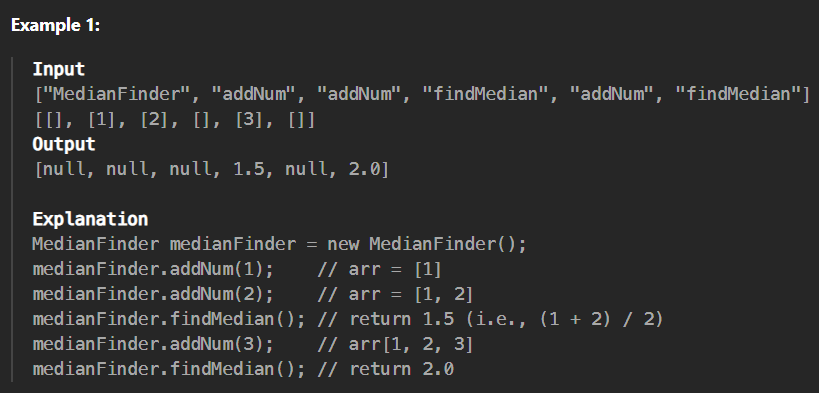
- 현재 존재하는 배열 내 중앙값을 찾아 반환한다.
- 배열의 원소는 추가될 수 있다.
- 위 조건에 부합하도록 MedianFinder 클래스를 만든다.
❓ 중앙값(Median)
배열 내 존재하는 원소의 개수가
홀수인 경우, 배열의 가운데 수 반환
짝수인 경우, 배열 가운데 두 수의 평균 반환
접근 1
- 원소는 무작위 들어올 테니, 이를 오름차순으로 저장하는 연결리스트를 생성
- 추가될 원소의 연결리스트 내의 위치는 이진탐색으로 찾자!
-> 원소를 정렬만 한다면 중앙값을 찾는 건 쉬울 것이라 판단하여
무작위로 추가되는 원소를 오름차순으로 정렬하는 데에 초점을 맞춤.
✍ 부분 코드 설명 1
변수 & 생성자 작성
class MedianFinder {
private List<Integer> list;
public MedianFinder() {
list = new ArrayList<>();
}
...
}- list: 원소들을 오름차순으로 저장할 연결리스트
addNum() & findMedian() 함수
public void addNum(int num) {
int idx = findIdx(num, 0,list.size()-1);
list.add(idx,num);
}
public int findIdx(int num, int start, int end){
if(start>end){
return start;
}
int half = (start+end)/2;
if(list.get(half)<num){
return findIdx(num,half+1, end);
}
else{
return findIdx(num, start, half-1);
}
}
public double findMedian() {
int size = list.size();
if(size%2==0){
int idx1 = size/2;
int idx2 = size/2-1;
return (double)(list.get(idx1)+list.get(idx2))/2;
}
else{
return list.get(size/2);
}
}addNum(): 현재 리스트에 추가할 원소의 위치를 찾는findIdx()함수 호출 후 해당 위치에 원소 저장findIdx(): 이진탐색을 통해 리스트 내 추가할 원소의 인덱스 찾아서 반환findMedian(): 리스트에 저장된 원소의 개수가 짝수인 경우, 가운데 두 수의 평균 반환
홀수인 경우 가운데 수 반환
✨ 결과 1
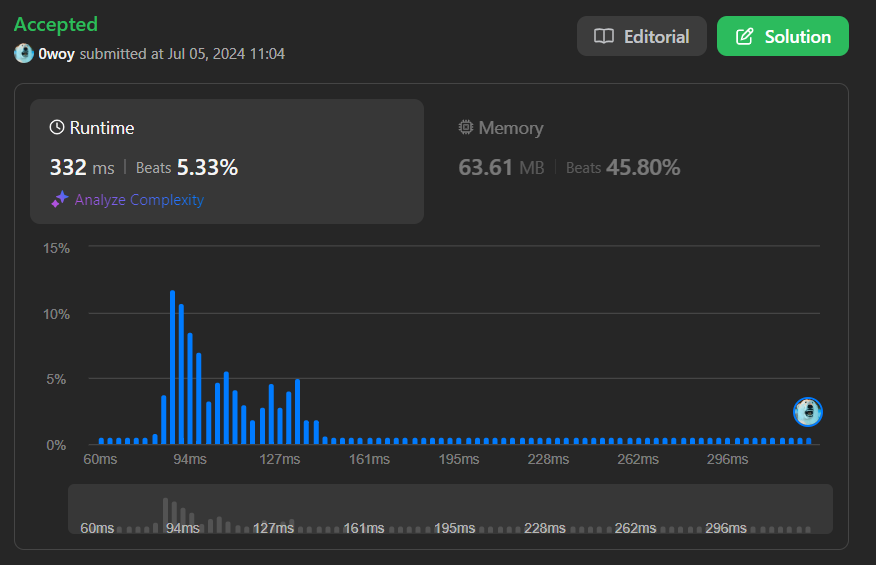
풀긴 풀었다만 뭔가 떨떠름한 RunTime 시간...

그래도 시도했다가 통과는 했으니까... 걍 넘어갈까말까 했지만
나보다 더 효율적인 다른 사람들의 풀이를 봤다.
풀이를 보니 세상엔 똑똑한 사람들이 많고... 이걸 이렇게 풀 수도 있구나 라고 생각했다.
접근 2
-
우선순위 큐 2개를 생성한다.
- max pq: min에 있는 수보다 작고, 우선순위가 내림차순으로 설정된 큐
- min pq: 우선순위가 오름차순인 큐 (default)
-
기본적으로 모든 숫자는 max에 먼저 삽입한다.
-
큐의 크기 차가 1을 초과하지 않도록 min에 max 큐에서 가장 큰 값을 삽입한다.
-
max < min인 경우 min에서 가장 작은 값을 max에 삽입한다.
max의 크기가 min보다 항상 크거나 같으므로
원소 개수가 홀수인 경우 max에서 가장 작은 값이 전체 원소의 중앙값이 된다.
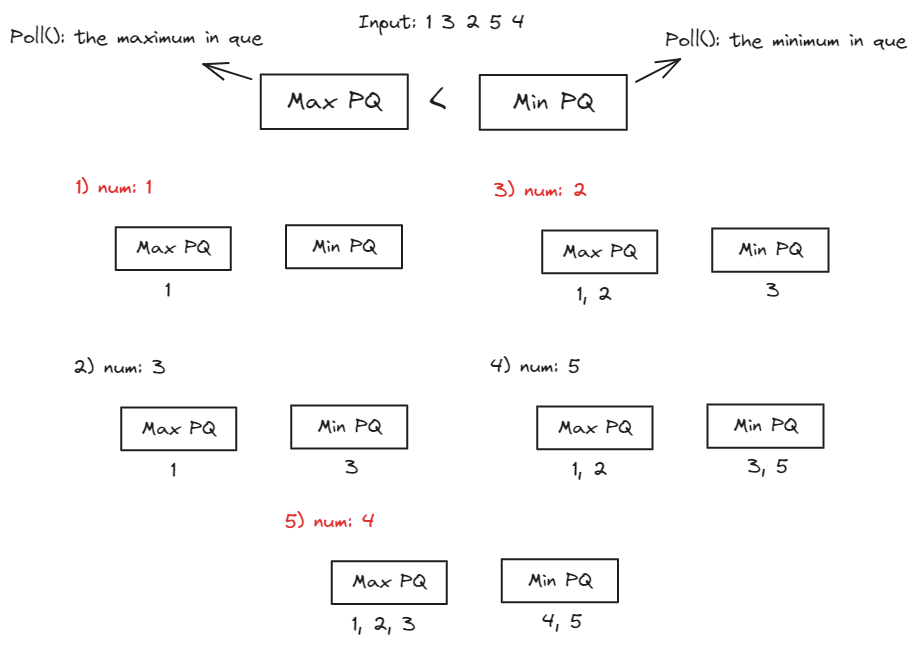
빨간 색은 max < min 조건에 걸려 min의 가장 큰 원소가 max로 넘어간 경우이다.
- 원소 개수가
짝수인 경우, max에서 가장 큰 값, min에서 가장 작은 값의 평균이 중앙값이 된다. 홀수인 경우는 max에서 가장 큰 값이 중앙값이므로 원소 개수에 따라 계산하여 반환하면 된다.
✍ 부분 코드 설명 2
변수 & 생성자 작성
class MedianFinder {
PriorityQueue<Integer> min;
PriorityQueue<Integer> max;
public MedianFinder() {
min = new PriorityQueue<>();
max = new PriorityQueue<>(Collections.reverseOrder());
}
...
}min: 가장 작은 수가 우선으로 선택되는 우선순위 큐max: 가장 큰 수가 우선으로 선택되는 우선순위 큐
addNum() & findMedian() 함수
public void addNum(int num) {
max.offer(num);
min.offer(max.poll());
if(max.size()<min.size()){
max.offer(min.poll());
}
}
public double findMedian() {
if(max.size()==min.size()){
return (max.peek()+min.peek())/2.0;
}
else{
return max.peek();
}
}-
addNum(): 추가된 num을 max에 삽입 후, max에서 가장 큰 수를 min에 삽입
min의 크기가 max보다 큰 경우, min에서 가장 작은 값을 max에 삽입한다. -
findMedian()
- max와 min의 크기가 같은 경우 (전체 원소가 짝수인 경우),
min에서 가장 작은 원소, max에서 가장 큰 원소의 평균을 반환한다.
- 홀수인 경우 max에서 가장 큰 값을 반환한다.
✨ 결과2
이렇게 푸니 다른 사람들과 비슷한 RunTime 시간을 갖는 게 보인다..
그런데 이진탐색이나 Heap을 사용한 addNum()의 시간 복잡도는 O(LogN)으로 같은데 왜 RunTime 시간에서 거즘 3배가 발생하는지 궁금해서 찾아봤다.
찾아본 결과, 나는 연결리스트를 이용하여 새로운 수가 들어올 때마다 적절한 위치를 찾아 list에 삽입했는데,
이렇게 중간에 원소를 삽입하면, 기존에 있던 원소들을 뒤로 밀어야 하는 재조정이 필요하다.
list의 구조를 재조정하는 시간때문에 RunTime 시간에서 차이가 났다.