자료구조와 알고리즘

2023학년 1학기, 자료구조 수업을 수강하면서 배운 내용을 노트 정리 후 간략(?)하게 velog에 올리고자 해당 POST를 작성합니다.
( 교재: C언어로 쉽게 풀어쓴 자료구조 )

프로그램 = 자료구조 + 알고리즘
알고리즘: 컴퓨터로 문제를 풀기 위한 단계적인 절차

---

📕 자료구조와 알고리즘

1) 알고리즘의 조건

• 입력: 0개 이상의 입력 존재
• 출력: 1개 이상의 출력 존재
• 명백성: 각 명령어의 의미는 모호하지 않고 명백
• 유한성: 한정된 수의 단계 후, 반드시 종료
• 유효성: 각 명령어들은 실행 가능 연산

2) 알고리즘의 기술방법

1. 자연어
   인간이 읽기 쉽다.
   정확히 전달하지 않으면 의미 전달이 모호할 우려가 존재함.

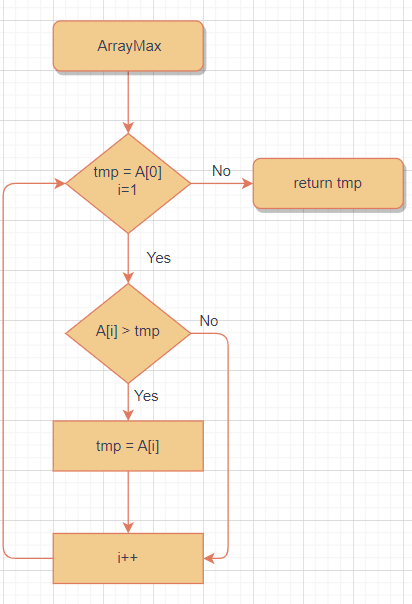
ArrayMax(list, N)
1. 배열 list의 첫번째 요소를 변수 tmp에 복사
2. 배열 list의 다음 요소들을 차례대로 tmp와 비교하여
더 크면 tmp로 복사
3. 배열 list의 모든 요소 비교 후 tmp 반환

2. 흐름도
   직관적이고 이해하기 쉬움
   복잡한 알고리즘의 경우 상당히 복잡해짐

3. 의사코드
   알고리즘 기술에 가장 많이 사용
   프로그램 구현시 여러 문제를 감출 수 있으므로
   알고리즘의 핵심적인 내용 에만 집중할 수 있음

ArrayMax(list, N):
	largest = list[0]
    for i=1 to N-1 do
    	if list[i]>largest
        	then largest = list[i]
    return largest

4. 프로그래밍 언어
   알고리즘의 가장 정확한 기술 가능
   실제 구현 시, 구체적인 사항들이 알고리즘의 핵심 내용에 대한 이해를 방해할 수 있음

   #define MAX_ELEMENTS 100
   
   int score[MAX_ELEMENTS];
   int find_max_score(int n){
   	int i, tmp;
     	tmp = score[0];
     	for(int i=1;i<n;i++){
      	if(score[i]>tmp)
         		tmp=score[i];                
      }
      return tmp;
   }

---

📗 추상 데이터 타입

📖 자료형

자료형 : 데이터의 종류
ex) 정수, 실수, 문자열 등

a) 기초 자료형: char, int, double 등
b) 파생 자료형: 배열, 포인터 등
c) 사용자 정의 자료형: 구조체, 공용체, 열거형 등

1) 추상 데이터 타입(ADT)

• 데이터 타입을 추상적(수학적)으로 정의한 것
• 데이터 or 연산이 무엇 인가는 정의 되지만, 어떻게 컴퓨터 상에서 구현할 것인지는 정의되지 않음

2) 추상 데이터 타입 정의

• 객체: ADT에 속하는 객체 정의
• 연산: 객체들 사이 연산 정의, ADT와 외부를 연결하는 Interface 역할

---

📘 알고리즘 성능 분석

1) 성능 분석 기법

1. 수행시간 측정

   i) 두 알고리즘의 실제 수행시간 분석
   ii) 실제로 구현 필요
   iii) 동일한 하드웨어를 사용해야 함

2. 복잡도 분석

   i) 직접 구현하지 않고 수행시간 분석
   ii) 연산횟수 측정 및 비교
   iii) 일반적으로 연산 횟수는 n의 함수이다

n의 함수?
수행 횟수는 고정된 상수가 아닌 입력 개수인 n의 비례하여 유동적이므로 n의 함수!

2) 복잡도 분석 종류

🕜 시간 복잡도 (Time Complexity) : 알고리즘의 수행시간 분석
📚 공간 복잡도 (Space Complexity) : 알고리즘의 기억공간 분석

공간복잡도보다 시간복잡도가 우선시 되어왔지만,
최근 공간 복잡도를 고려하는 것도 중요해 지고 있다.
왜냐면 웨어러블 기기(애플 워치 등)이 널리 사용되면서 공간을 생각해야 함

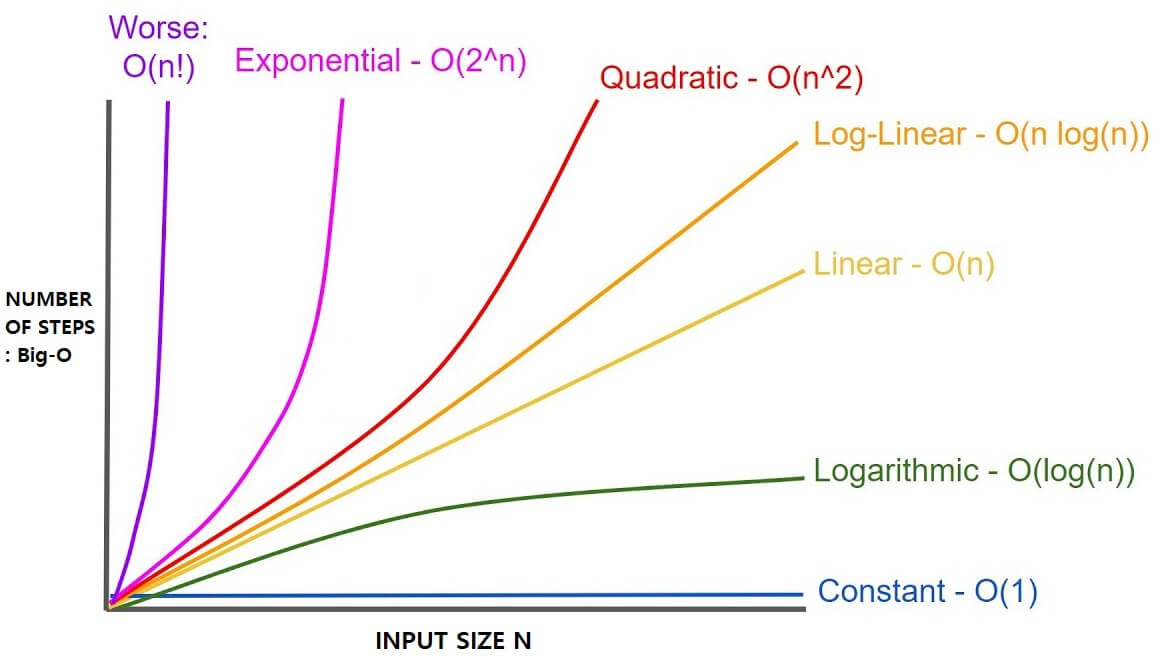
3) 빅오 표기법

• 빅오 표기법: 연산 횟수를 대략적(점근적)으로 표기

  일반적으로 n과 시간복잡도 T(n)의 관계는 상당히 복잡하다.
  하지만 n이 커질 수록 차수가 가장 큰 항이 시간복잡도에 가장 많은 영향을 주므로 보통 T(n)에서 차수가 가장 큰 항만을 고려하면 충분하다.

• 두 함수 f(n)과 g(n)이 주어졌을 때, 모든 n >n0에 대해 |f(n)| <= c|g(n)| 을 만족하는 n0와 c가 존재 한다면 f(n) = O(g(n))

//예제
f(n) = 3n² +100
3n² +100 <= 5n² (n>9) 
=> O(n²) 

4) 자주 사용되는 빅오 표기법

• O(1) : 상수형
• O(logn) : 로그형
• O(n) : 선형
• O(n logn) : 선형 로그형
• O(n² ) : 2차형
• O(n³) : 3차형
• O(2ⁿ ) : 지수형
• O(n!) : 팩토리얼 형

🚫 주의!
상수항이나 계수가 굉장히 큰 경우, 수행시간에 영향을 끼친다.

//예시
//A가 더 효율적인 경우: n>100일 때
A: 3n + 100, O(n)
B: 5n², O(n²)

5) 최선, 평균, 최악의 경우

• 최선의 경우: 의미 없는 경우가 많다
• 평균의 경우: 계산하기 상당히 어렵다.
• 최악의 경우: 가장 널리 사용된다.

---

📖 출처

빅오 표기법 그래프: https://iq.opengenus.org/time-complexity-analysis/